总览
课程成绩
1、线上单元测试32分(每单元4题,题型有单选、多选、判断、填空题。每题1分,客观题,题库随机抽题)
2、线上讨论8分(讨论题2题,每题回帖100字以上)
3、线上期末考试40分(客观题40题,全覆盖,题库随机抽题)
4、课后作业20分(主观题2题,线上提交,老师批改)
【ddl为结课后一周,实际上可以全部留到最后一周做完】
教学概况
授课老师:蒋文华,浙江大学公共管理学院城市管理和发展系,1991年开始从事高校教学。
不点名,没有考勤分数。一些小测题会和上课实际内容相关,但题库疑似每年不改(所以不去其实也没事)。
上课会玩发红包游戏,基本10元以内,自愿参加。
第一讲 概述
一、何为“博弈”
博:博览全局;弈:对弈棋局。指在一定规则约束下,基于直接相互作用环境,各参与人依据所掌握信息,选择策略实现利益最大化。
博弈是指在一定的游戏规则约束下,基于直接相互作用的环境条件,各参与人依据所掌握的信息,选择各自的策略(行动),以实现利益最大化的过程。
博弈就是你中有我,我中有你。由于直接相互作用,每个博弈参与者的得益不仅取决于自己采取的策略(行动),还取决于其他博弈参与者所采取的策略(行动)。博弈的核心在于基于整体思维基础上的理性换位思考,你应当用他人的得益去推测他人的策略(行动),从而选择最有利于自己的策略(行动)。
博弈论(game theory)——一是一种研究人们怎么做策略(行动)选择及其均衡结果会是什么的理论。
- 博弈双方需博览全局(即考虑整体局势)并对弈棋局(采取具体行动)
- 各参与人的决策存在直接相互作用(一个参与人的变化会引起其他参与人的变化)
- 利益关系可以是对立的竞争关系,也可以是一致的合作关系
- 博弈既可以是竞争,也可以是合作!利益对立时竞争,利益一致时合作。
- 双赢是合作的结果(利益一致),单赢是竞争的结果(利益对立)。
- 世上有两种博弈:有限游戏以取胜为目的,无限游戏以共赢为目的。
- 市场经济本质是通过卖者之间(买者之间)的竞争,实现买卖双方的合作。
- 商业竞争不以消灭对手为目的,而更像体育竞技,有对手无敌手。
- 失败者的教训是社会财富创造的重要源泉。
- 选对市场(对手)比选对策略更重要(股市/房市),选对博弈(game)比选对策略更重要。
- 学习博弈论有助于我们更好地与他人合作,教育的最终目标是激发潜能和善意。
二、发展简史
博弈论一开始是经济学(寡头竞争)的重要分析工具,现在已经发展成各门社会科学(管理学、公共管理学、政治学、法学、社会学等)的基本分析方法和重要研究工具。30年来共有20位经济学家因在博弈论及直接相关领域(如激励理论、拍卖理论)的贡献而获得诺贝尔经济学奖(1994、1996、2001、2005、2007、2012、2014、2016、2020年)。
最初探索
- 古诺模型(Cournot Model,1838年):研究双寡头垄断市场中企业产量决策的模型,企业以各自在同一时间内相互独立的产量作为决策变量。
- 伯川德模型(Bertrand Model,1883年):与古诺模型不同,企业把产品的价格而非产量作为竞争手段。其结论即伯川德悖论(Bertrand Paradox)表明,在完全竞争市场中,寡头企业会相互削价,直至价格等于边际成本,长期经济利润为零。
- 斯塔克尔伯格模型(Stackelberg Model,1934年):动态博弈模型,分析双寡头市场竞争中企业间行动次序的区别,领导者厂商决定产量后,跟随者厂商根据领导者产量决定自身产量。
诞生与发展
- 20世纪40年代的社会变化(寡头竞争、世界大战)促使对系统研究方法的需求。
- 约翰·冯·诺依曼(John Von Neumann)和摩根斯坦发表《博弈论和经济行为》(1944年),标志博弈论正式诞生。
- 约翰·福布斯·纳什(John Forbes Nash)提出纳什均衡概念,对博弈论进行发扬光大。以博弈论创始人纳什为原型的电影:《美丽心灵》。
- 后来的发展方向包括对纳什均衡的弱化、精炼、基本假设研究及应用研究。
第二讲 术语解读和基本假设
一、术语解读
博弈论的基本术语
- 参与人(Players):博弈中的决策主体,如企业、国家或个人。
- 信息(Information):参与人对博弈的知识,包括其他参与人的特征、策略和收益等。
- 行动(Actions):参与人可选择的变量,如出价、产量等。
- 策略(Strategies):参与人的行动规则,即在行动前准备好的完整行动方案。
- 损益(Payoffs):参与人的得与失,是所有参与人策略的多元函数。
- 结局(Outcome):所有参与人选择策略后的结果。
- 均衡(Equilibrium):所有参与人的最优策略组合,此时无人能通过改变策略增加收益(又称“僵局”)。为局外人(研究者)所关心。
- 博弈规则(Rules of the Game):参与人(players)、行动(actions)、损益(payoffs)和信息(information)统称为博弈规则。简写为PAPI。
规则是一种人为的限制,对资格(行为主体)的限制,对行动空间(选择空间)的限制,对信息空间的限制,并建立起行动与损益之间的映射关系。
作为动词的博弈是指参与人在给定的博弈中选择策略及行动。 作为名词的博弈(game)是三个集合的集合:参与人集合+策略空间集合+损益函数的集合。博弈G=[S,…,Sn:U, …,Un]
二、博弈分类
合作博弈与非合作博弈
- 合作博弈(Cooperative Game):参与者能达成有约束力的协议,共同选择有利策略。
- 非合作博弈(Non-cooperative Game):参与者无法达成此类协议,但其中也可存在合作关系。
静态博弈与动态博弈
- 静态博弈(Static Game):参与者同时选择行动,或虽非同时但逻辑上同时。
- 动态博弈(Dynamic Game):参与者行动有先后顺序,后行动者可观察先行动者的行动。
特别提示:
- 静态博弈中,你是game的taker(接受者)。
- 动态博弈中,你既是当下game的taker,也是后续game的maker(创造者)。
- 博弈论让我们拥有动态思维:果上随缘,因上努力。
基于信息状况的分类
- 完美信息(Perfect Information):动态博弈中无外部和策略不确定性,每个信息集都是单点集。
- 不完美信息(Imperfect Information):存在某种不确定性,静态博弈一定是不完美信息。
- 不完全信息(Incomplete Information):事前存在不确定性,与完全信息相对。
- 对称信息(Symmetric Information):所有参与者拥有相同信息。
- 不对称信息(Asymmetric Information):参与者拥有不同信息。
零和博弈与非零和博弈
- 零和博弈(Zero-sum Game):博弈前后损益总和相等,如赌博、金融市场。
- 非零和博弈(Non-zero-sum Game):博弈后损益总和大于或小于初始总和,分为正和或负和。
eg:
- 打麻将:家里打——正和;棋牌室打——负和
- 买彩票、炒股:负和(大部分人永远是亏的)
特别提示:不玩负和游戏,少玩零和游戏,多玩正和游戏。
三、基本假设
理性假设
- 认知理性:
- 人是自我利益的判断者。
- 偏好具备完备性、传递性和凸性(综合激励)。
- 行为理性:
- 自我利益的追求者(行为者)。
- 追求利益最大化(期望效用最大化),但期望效用和期望收益不一定相同。
特别提示:
- 两利相权取其重,两害相权取其轻。
- 顾客需要的不是便宜,而是占到了便宜。
共同知识假设
共同知识(Common Knowledge):各参与人在无穷递归意义上均知悉的事实。不同于共有知识(Mutual Knowledge),共同知识需要信息在参与者间达到无限层次的相互知晓。
特别提示:
- 理性共识:参与者对博弈规则和彼此理性有共识。
- 规则共识:参与者对博弈的具体规则有共识。
第三讲 囚犯困境和破解之道
一、囚犯困境
囚犯困境是博弈论中的经典例子,展示个体理性选择可能导致集体非理性结果。
基本场景如下:
两名犯罪嫌疑人共同作案后被警方抓获,但警方证据不足,只能将他们隔离审讯,分别提出相同的交易条件:
如果两人都坦白交代犯罪事实,各判有期徒刑5年;
如果一方坦白而另一方抵赖,则坦白者因立功表现将刑期减至1年,而抵赖者因证据确凿将被判重刑10年;
如果两人都抵赖,警方只能以较轻的证据不足罪名各判1年有期徒刑。
在这种情况下,每个囚犯都有两种策略选择:坦白或抵赖。无论对方作何选择,对个人最有利的策略都是坦白,这就是所谓的占优策略。然而,当双方都选择占优策略坦白时,最终结果却是各判5年,比相互抵赖各判1年的结果要差。这体现了个体理性选择与集体理性结果之间的冲突,是囚犯困境的核心所在。
其基本结构如下:
| 坦白 | 抗拒 | |
|---|---|---|
| 坦白 | P, P | T, S |
| 抗拒 | S, T | R, R |
其中,T(temptation)> R(reward)> P(punishment)> S(sucker)。
形成原因 :囚徒困境的根本原因在于私人成本与社会成本的差异,即个人行为的负外部性。个体理性选择导致了集体非理性结果,双方都选择占优策略,却导致更差的结果。
特别提示:
- 表面上看囚犯对自身利益的追求是导致囚犯困境的原因。然而,真正的原因在于:囚犯们在追求自身利益的同时,是以更多地损害他人利益为代价。
- 囚犯困境的根本原因在于:私人成本与社会成本的差异,即个人行为的(强)负外部性。
占优策略
占优策略 :无论其他参与人采取什么策略,某个参与人的某种策略都能给他带来比其他策略更大的收益,该策略就是他的占优策略。在囚徒困境中,坦白就是每个囚徒的占优策略。
占优策略均衡 :是比纳什均衡更严苛的一种均衡。如果无论其他参与人采取什么策略,每个参与人都有唯一的占优策略,那么这些占优策略组合起来,就构成占优策略均衡。囚徒困境是占优策略均衡的经典例子。
纳什均衡
纳什均衡描述了一种在多人决策中的稳定状态。在这个状态下,每个参与者都选择了针对其他参与者策略的最佳应对策略。假设有一群人参与博弈,每个人都需要选择自己的策略。当所有其他人的策略都确定后,没有任何一个人可以通过改变自己的策略来获得更好的结果。也就是说,每个人都认为自己已经做出了最优的选择,基于其他人的行为。此时,这个策略组合就是一个纳什均衡。
- 对比与分析
- 占优策略 适用于任何情况下都优于其他策略,不需要考虑其他参与人的策略选择。
- 纳什均衡 则需要考虑其他参与人的策略,并在此基础上选择最优策略。
- 占优策略均衡是一种特殊的纳什均衡,但并非所有纳什均衡都是占优策略均衡。
- 占优策略均衡不需要理性共识,纳什均衡需要理性共识。
- 占优策略均衡不需要理性共识,即不需要假设其他参与人是理性的;而纳什均衡需要理性共识,即每个参与人都假设其他参与人是理性的,并且这种理性是共同知识。
二、如何破解囚徒困境
破解之道包括道德教化、制度建设和温故知新(如重复博弈)。
特别提示:
- 损人利己和损己利人本质上是一样的,是一个硬币的正反两面;从一方来看是损己利人的行为,在另一方来看是损人利己的行为,问题的关键是所损(失)的部分和所利(得)的部分哪个更多。(盗窃与抢劫)。
- 道德教化需长期保持一定比例的利他主义者以维持社会稳定。
- 制度建设如圈地运动减少负外部性、人民公社的自由退社权、第三方执行机制等。
- 重复博弈可让历史指导未来,学习博弈论课程有助于理解其中规律。
- 民主必须与法治(而非仅仅是法制)相辅相成,才能避免多数人的暴政。
- 国家理论指出,人类社会发展中的交易执行方式可分为基于道德自律、相互制约和第三方监督三类,而国家的出现与第三方监督密切相关。
第四讲 万元陷阱和智猪博弈
一、万元陷阱
万元陷阱是耶鲁大学经济学家苏必克发明的拍卖游戏,其规则是将10000元进行英国式拍卖,出价最高者获得该笔钱,同时出价第二高者需支付其出价金额。这个游戏常导致参与者陷入不断加价的陷阱,最终付出沉重代价。
自古以来,人类为捕杀动物所设的陷阱,有三个特征:
1.有一个明显的诱饵。
2.通往诱饵之路是单向的,可进不可出。
3.越想挣脱,就越陷越深。
4.只要有沉没成本就会有万元陷阱
社会心理学家泰格(A.Teger)对参加拍卖游戏的人加以分析,发现掉入‘陷阱’的人通常有两个动机:
一是经济(理性)的、二是非经济(感性)的。
经济动机:渴望赢得钞票、想赢回他的损失、想避免更多的损失
非经济动机:渴望挽回面子、证明自己是最好的玩家及处罚对手等。
心理学家鲁宾(J.E.Rubin)的建议是:
1、确立你投入的极限及预先的约定:譬如投资多少钱或多少时间?
2、极限一经确立,就要坚持到底。(止损)——止盈容易止损难
3、自己打定主意,不必看别人。
——学会止损,会让你活的更久
止损难的原因:贴现、人对亏损和盈利的敏感程度不同——一旦亏了就会偏好风险
特别提示:
- 序位竞争(如排名赛)容易产生万元陷阱。
- 竞技体育是典型的万元陷阱。
- 掉入陷阱的人通常受经济动机(如渴望赢得钞票、挽回损失)和非经济动机(如挽回面子、证明自己)驱动。
- 心理学家建议确立投入极限并坚持止损,避免目标偏移。
二、智猪博弈
智猪博弈描述了一种搭便车现象,其中一方付出代价而双方共享收益。
场景如下:
假设有一间猪圈,圈里养着一头大猪和一头小猪。猪圈的一头有一个按钮,另一头则放置着饲料槽。按动按钮后,饲料槽处会有饲料流入。但按下按钮需要付出一定的成本,比如耗费体力或者时间。
小猪和大猪都面临一个选择:要么去按按钮,要么在饲料槽处等待。如果小猪去按按钮,大猪在饲料槽等待,那么大猪将独享绝大部分饲料,而小猪只能在按完按钮后赶到饲料槽,吃剩下的一小部分饲料;如果大猪去按按钮,小猪在饲料槽等待,小猪将能独享绝大部分饲料,而大猪在按完按钮后只能吃剩下的一小部分;如果两只猪都选择等待,那么饲料槽处不会有饲料流入,两只猪都吃不到饲料;如果两只猪都选择去按按钮,那么它们都会付出成本,但饲料流入后它们都能吃到一些饲料。
其基本结构如下:
| 小猪按 | 小猪等 | |
|---|---|---|
| 大猪按 | 9, 1 | 7, 3 |
| 大猪等 | 6, 4 | 0, 0 |
特点:
- 多劳不多得:小猪选择等待,大猪去按按钮,最终小猪获得6单位收益,大猪获得4单位收益。
- 个体理性与集体理性相冲突:小猪有动机等待,而大猪不得不按按钮,导致大猪付出更多却收益较少。
eg:
- 山寨现象:盗版产品可以看作是对原创产品的“搭便车”,原创者付出努力却收益较少。
- 网络购物:后买者可以参考先买者的评价,先买者付出时间和精力,后买者获得信息收益
特别提示:
- 个体理性与集体理性是否冲突取决于制度安排。
- 解决冲突需修改游戏规则,满足个体理性基础上实现集体理性。
- 收入分配不均有助于减少个体与集体理性的冲突。
第五讲 懦夫博弈和夫妻博弈
一、懦夫博弈
懦夫博弈,也称斗鸡博弈(Chicken Game)是描述竞争关系的博弈模型。
基本场景如下:
两名司机分别驾驶一辆汽车,朝着对方疾驰而来,道路狭窄,无法同时通过。每个司机都有两种选择:要么继续向前开,要么在最后一刻后退。如果两人都选择后退,那么他们都能安全通过,但会感到有点羞愧;如果一方转向而另一方继续向前,那么后退的人会被嘲笑为“懦夫”,而继续向前的人则会被称为“英雄”;如果两人都选择继续向前,那么他们将发生严重碰撞,两败俱伤。
其基本结构如下:
| 进 | 退 | |
|---|---|---|
| 进 | -5,-5 | 10,0 |
| 退 | 0,10 | 0,0 |
特点:
- 纳什均衡:有两个纯策略纳什均衡,即(退,进)和(进,退)。
- 风险与收益:选择进可能获得高收益,但也面临高风险;选择退则收益较低,但风险较小。
模型拓展:
- 多次博弈:如果懦夫博弈进行多次,冒险选择向前而成功的参与人可能更有信心在未来采取这种策略。
- 信号传递:通过发出信号让对方相信自己不会退,可以迫使对方选择退。
eg:
- 路权之争:两车在狭窄道路上相向而行,互相不让道,最终可能通过一方转向来避免事故。
- 公共物品提供:在提供公共物品时,各方可能通过懦夫博弈来决定是否愿意承担成本。
启发:
- 奖励适度:过高的奖励可能导致过度竞争,适得其反。
- 先动优势:在竞争中抢占先机,可以获得更大的收益。
特别提示:
- 先下手为强,后下手遭殃。
- 竞争博弈中,领先一步、高人一筹至关重要。
- 均衡解中,进的概率和期望收益取决于具体参数。
二、夫妻博弈
夫妻博弈是描述合作博弈的经典模型。
基本场景如下:
夫妻二人计划晚上一起看电视节目。丈夫更喜欢看一场激烈的足球比赛,而妻子更倾向于观看一部浪漫的芭蕾舞剧。不过,无论看什么节目,他们都希望能一起观看。如果两个人各自看自己喜欢的节目,他们都会不开心。这种情况下,夫妻二人需要进行夫妻博弈,来决定最终观看哪个节目。
其基本结构如下:
| 足球 | 芭蕾 | |
|---|---|---|
| 足球 | 2,1 | 0,0 |
| 芭蕾 | -1,-1 | 1,2 |
特点:
- 纯策略纳什均衡:有两个,即(足球,足球)和(芭蕾,芭蕾)。
- 混合策略纳什均衡:男以2/3概率选择足球,女以2/3概率选择芭蕾。
- 家庭地位与先动优势:家庭地位较高的一方可能具有先动优势,决定最终的均衡结果。
- 轮流选择与随机选择:轮流去对方喜欢的地方或随机选择,可以避免矛盾冲突。
启发:
- 合作与共赢:夫妻博弈是合作博弈,双方需要在共同利益的基础上,协商选择结果。
- 提前约定收益分配:提前约定合作收益的分配机制,可以降低合作成本,避免矛盾
特别提示:
- 合作需要沟通与协调,但沟通协调成本过高则合作难成。
- 人类社会制度和技术演进方向是降低沟通协调成本。
- 合作博弈核心问题在于合作剩余分配和合作风险分担。
三、猎鹿博弈
猎鹿博弈(Stag Hunt) 是描述合作博弈的经典模型,其基本结构如下:
| 猎鹿 | 猎兔 | |
|---|---|---|
| 猎鹿 | 4, 4 | 0, 2 |
| 猎兔 | 2, 0 | 2, 2 |
特别提示:
- 两个猎人合伙猎鹿一定是最优结果。但一方选择去猎鹿的前提是他能够预期到对方会选择猎鹿,而对方选择去猎鹿的前提也是预期到另一方会去猎鹿。也就是说,只有“双方都去猎鹿”成为一个共同知识的前提下,这个最优结果才会如期出现。
- 在没有沟通(独立决策)的情况下,每个猎人选择猎鹿的概率是50%。每个人选择猎鹿的期望收益也就是2只兔子。对于任何一方来说,出于风险规避的考虑(一般而言,人是厌恶风险的),还不如独自去猎兔。当双方都意识到这一点后,一起去猎鹿反而变得不可能了。
- 为了让双方都有一个更好的结果,出发之前提前沟通就变得非常重要了。如果双方提前约好一起去猎鹿,那么都选择猎鹿就是一个均衡结果。此时,没有人愿意偏离这个结果而选择去猎兔。
- 沟通是有成本的。在这个例子中,如果每人所承担的沟通成本小于2只兔子(总成本小于4只兔子),提前沟通能够提高双方总的收益水平,反之还不如分头去猎兔。
特别提示:
- 合作博弈的核心问题:
- 合作剩余(新增收益)怎么分配?
- 合作风险怎么分担?
- 合作需要沟通与协调,但沟通协调成本过高,合作很难成功。
- 人类社会制度和技术的演进方向:不断降低人与人之间的沟通(协调)成本。
四、鹰鸽博弈
鹰鸽博弈(Hawk-Dove Game) 是描述竞争关系的博弈模型,其基本结构如下:
| 老鹰 | 鸽子 | |
|---|---|---|
| 老鹰 | A-C, A-C | 2A, 0 |
| 鸽子 | 0, 2A | A, A |
特别提示:
- 当A > C时,老鹰—老鹰是纳什均衡。
- 当A < C时,老鹰策略的概率α* = A/C。
- 损失更大的一方更愿意选老鹰。
推论:
- 恶霸博弈中,谁损失大,谁获益多。
- 你的决策成本由他人决定,你的决策由他人的成本决定。
第六讲 最后通牒与讨价还价
一、最后通牒
最后通牒(Ultimatum Game)是分配固定金额的博弈,一方提出方案,另一方决定接受或拒绝。若拒绝,双方均一无所获。
eg:两个人分一笔总量固定的钱(如 100 元),一个人作为提议者提出分配方案,另一个人作为响应者进行表决。若响应者同意,则按提议者的方案分配;若不同意,则两个人都一无所有。
实验表明:
- 大多数人提出的分配方案在 40%-50% 之间。
- 少数人提出 50% 以上的分配方案。
- 当分配方案低于 20% 时,被拒绝的概率很高(40%-50%),随着分配金额的减少,拒绝的可能性逐渐增加。
独裁者博弈
独裁者博弈是最后通牒博弈的变体,提议者决定分配方案,响应者只能接受,无拒绝权。
特点:
- 提议者拥有绝对权力决定分配。
- 响应者无法影响分配结果。
实验观察:尽管提议者可独占所有资源,但许多提议者仍选择给予响应者一定份额,反映出人们内在的公平意识和利他倾向。
推论:
- 提议者的行为受道德和社会规范影响。
- 制度设计应考虑如何通过规则促进公平与合作。
特别提示:
- 越是成熟的组织,在管理中越倾向于运用最后通牒。
- 最后通牒可节省谈判成本并提供公平感。
- 出价高低受贪婪与恐惧影响。
- 权力基础影响分配结果,如随机分配或基于智力测试等。
- 谁承担决策的后果(出了问题谁负责?),谁负责决策
二、讨价还价
讨价还价(Bargaining)是参与者通过协商解决利益分配问题的过程。
eg:
选项 A:今天得到 100 元。(82% 的人选择)
选项 B:4 周后得到 110 元。(18% 的人选择)
谈判成本:谈判过程是有成本的,包括时间、精力的消耗等,这可能会影响双方是否愿意进行谈判以及谈判的最终结果。
贴现因子:是指一个份额经过一段时间后所等同的现在份额,它反映了参与者的“耐心”程度。贴现因子由多方面因素决定,如年龄、财富、未来收益的确定性以及知识水平等。
影响贴现因子的因素
- 年龄(寿命):寿命越长,越看重长远利益。
- 财富:越富有,越关注长远利益。
- 未来收益的确定性(法治):确定性高,则更看重长远利益。
- 知识水平(文化程度):知识水平高,越看重长远利益。
特别提示:
- 讨价还价需考虑贴现因子,即 future gains 的当前价值。
- 贴现因子由参与者的耐心程度决定。
- 组织较个人有更长寿命预期,提高了贴现因子。
- 影响贴现因子的因素包括年龄、财富、未来收益确定性和知识水平。
第七讲 混合策略与监督博弈
一、混合策略
混合策略指参与者在给定信息情况下,以某种概率分布随机选择不同行动。与之相对的是纯策略,即在每一信息情况下只选择一种特定行动。
特别提示:
- 混合策略的目的在于防人(减少被伤害)。
- zju课程发现石头剪刀布的制胜策略:输家换用能胜对方的行动,赢家保持现状。
二、监督博弈
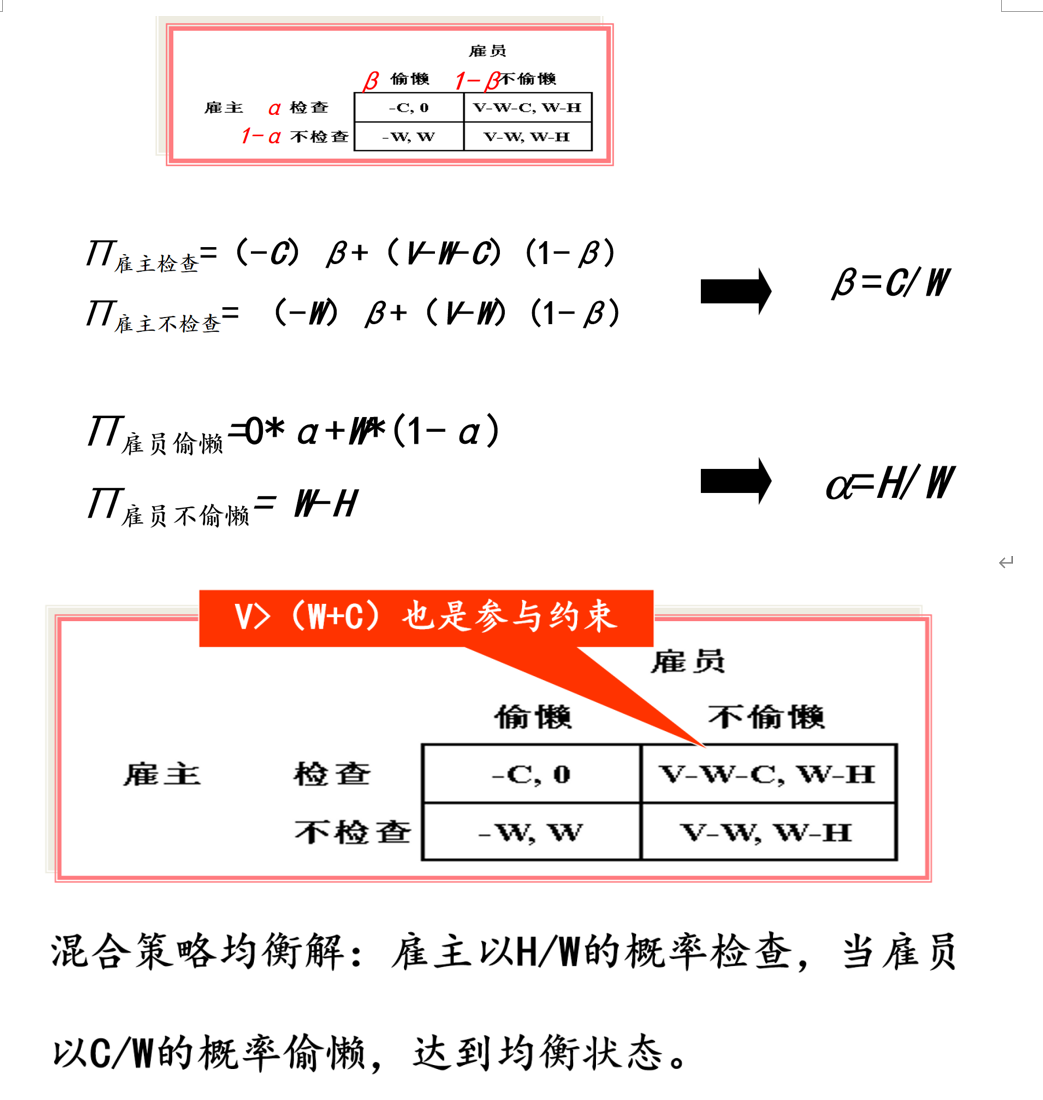
监督博弈涉及雇主和雇员间的监督与偷懒行为。其基本模型如下:
| 偷懒 | 不偷懒 | |
|---|---|---|
| 检查 | -C, V-W-C | -C, V-W-C |
| 不检查 | W, W-H | W, V-W |
特别提示:
- 混合策略均衡解中,雇主检查概率为 H/W,雇员偷懒概率为 C/W。
- 雇主支付工资 W 的期望收益最大值需通过求导确定。
- H越大,雇主越容易检查。
- C越大,雇员越容易偷懒。
- W越大,雇员越少偷懒,雇主越少检查。
第八讲 重复博弈和制度建设
一、重复博弈
重复博弈指同样结构的博弈重复多次,每次称为“阶段博弈”。其基本特征包括:
- 前一阶段博弈不改变后阶段结构。
- 所有参与人可观察过去历史。
- 总损益是各阶段损益的贴现值之和。
策略
重复博弈中可选择的策略。
雷锋策略:永远选择合作
曹操策略:永远选择背叛
冷酷策略(grim strategies),又叫触发策略:先选择合作,一旦被背叛就一直选择背叛(世上最冷酷的事:每个人都只有一条命)
心太软策略:偶尔一次背叛可以原谅,但连续两次背叛就会选择背叛
一报还一报(Tit-for tat):第一次合作,接下来你怎么对我,下一次我就怎么对你
人鬼策略:合作的多是人,背叛的多为鬼
欺软怕硬(又叫检验者战略,Tester):第一次背叛,看你是否好欺负,好欺负就背叛,不好欺负就合作
镇定者策略:先建立信任关系,然后想办法占小便宜
精神病患者(醉汉策略):随机合作或者背叛
囚犯困境的重复博弈
在重复博弈中,参与者的策略可以基于以往的互动历史。例如,“一报还一报”策略:
- 第一次选择合作。
- 之后的每一轮都模仿对方在前一轮的选择。
这种策略的特点:
- 它是善良的,不主动背叛。
- 它是可激怒的,对背叛行为做出反应。
- 它是宽容的,允许对方改正错误。
- 它是清晰的,易于理解和预测。
特别提示:
- 在一次性博弈中,背叛是占优策略;但在重复博弈中,可选择如冷酷策略、一报还一报等策略。
- “一报还一报”策略因其善良性、可激怒性、宽容性和清晰性,在重复博弈中表现优异。
二、制度建设
制度建设是博弈论的重要应用,旨在通过规则设计引导社会整体福利增加。
特别提示:
- 游戏规则决定游戏结局。
- 制度可修改完善,行为背后有原因,需从制度中寻找。
- 外因是条件,内因是根据,改变行为需提供足够激励(机制)。
- 制度好坏取决于是否鼓励通过说谎、偷懒获利,社会制度优劣评判标准在于此。
拍卖理论
Auction Theory
- 英国式拍卖(English Auction):从低往高叫价,直到没有人加价为止。
- 荷兰式拍卖(Dutch Auction):卖家叫价,从高往低,直到有人愿意交易为止。
- 最高价封标拍卖(First-price Sealed-bid Auction):投暗标,和最高价成交。
- 第二高价封标拍卖(Vickrey Auction):卖给最高价者,但以第二高价成交。
维克里拍卖(Vickrey Auction) 的优点:
- 信息披露真实。
- 信息披露迅速。
- 交易成本下降(时间成本、心理成本)。
- 买者满意度高。
制度的优劣评判
评判社会制度的优劣:
- 是否鼓励人们通过说谎来获利(隐藏信息)。
- 是否激励人们通过偷懒来获利(隐藏行动)。


