CV(1)：CV知识简介

参考
- showmeai-斯坦福CS231n教程

发展历程

历史

16世纪最早的相机：暗箱
(小孔成像)

1963年第一篇计算机视觉博士论文「Block world-Larry Roberts」，视觉世界简化为简单的几何形状，识别它们，重建这些形状。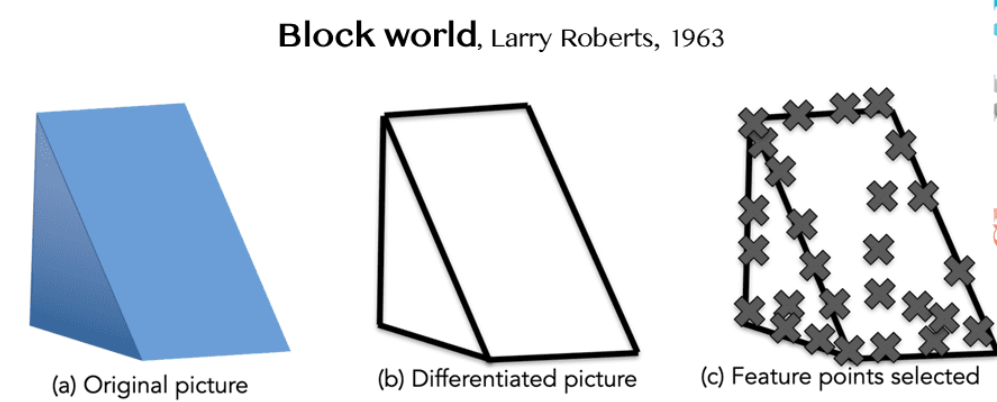

1966年MIT暑期项目「The Summer Vision Project」目的是构建视觉系统的重要组成部分。

1970s MIT视觉科学家David Marr编写了《VISION》，提出了视觉表现的阶段，如原始草图、零交叉点、圆点、边缘、条形、末端、虚拟线、组、曲线边界等概念。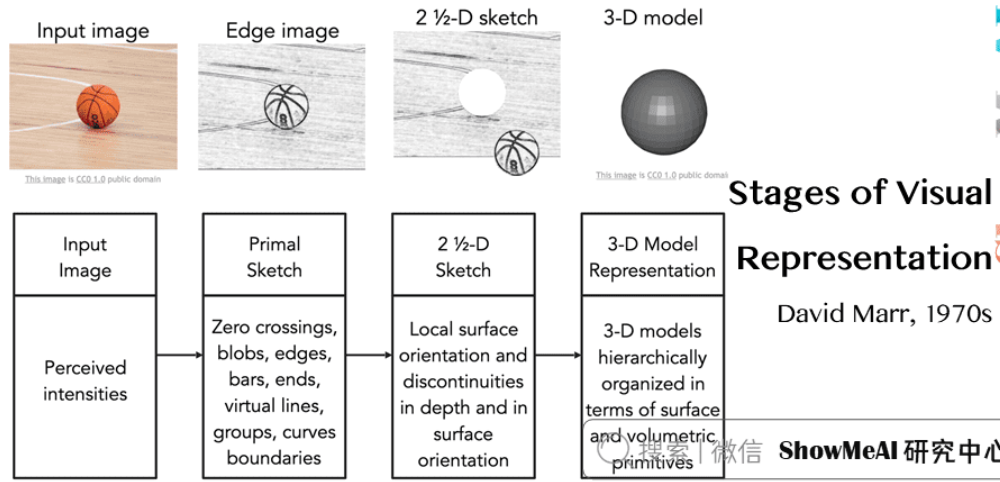

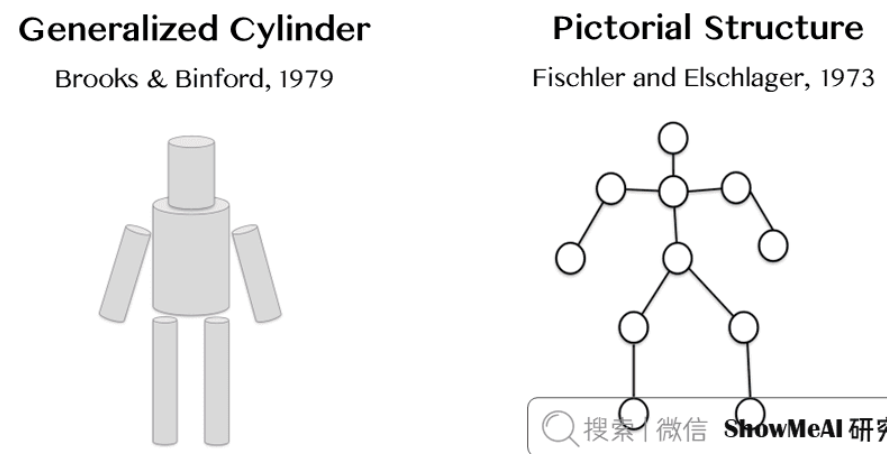
1973年后，斯坦福科学家提出 **「广义圆柱体」**和 「圆形结构」，每个对象都是由简单的几何图形单位组成。

1987年David Lowe尝试用线和边缘来构建识别。

1997年Shi & Malik提出，若识别太难了，就先做目标分割，即把一张图片的像素点归类到有意义的区域。

2001年机器学习快速发展（尤其是统计学习方法），出现了SVM（支持向量机）、boosting、图模型等。Viola & Jones发表了使用AdaBoost算法进行实时面部检测的论文「Face Detection」，2006年富士推出可以实时面部检测的数码相机。

1999年David Lowe发表**”SIFT” & Object Recognition**，提出SIFT特征匹配，先在目标上确认关键特征，再与相似目标匹配，完成目标识别。从90年代到2000年，思想是基于特征的目标识别。

【目标分割与特征识别】
目标分割：

定义：在图像中识别和标记出每个像素属于哪个对象，通常通过像素级分类实现。

方法：如U-Net、Mask R-CNN等语义分割模型，输出每像素类别标签。

结果：输出与输入图像同尺寸的分割图，每像素分配类别，实现像素级识别。
基于特征的目标识别：

定义：检测和识别特定对象，提取特征并与类别匹配。

方法：如Faster R-CNN、YOLO等对象检测模型，输出对象位置和类别。

结果：输出边界框，指示对象位置和类别。

2006年Lazebnik, Schmid & Ponce发表「Spatial Pyramid Matching」，通过空间金字塔匹配算法将图片各部分特征组合，作为特征描述符，再用SVM分类。

2005年后，方向梯度直方图和可变形部件模型用于人体姿态识别。

21世纪早期，数码相机发展，图片质量提升，出现了标注数据集。PASCAL VOC有20个类别，每类成千上万图片，推动算法发展。

普林斯顿和斯坦福提出识别大部分物体，机器学习易过拟合，部分原因是数据复杂、模型高维、参数多，训练数据不足时易过拟合，难以泛化。

Justin教授认为，CV发展主要取决于三个因素：算法、数据、计算，对应深度学习、ImageNet、GPU。
李飞飞：两方面动力：①识别万物；②克服过拟合。

ImageNet项目收集上亿张图片，用WordNet排序，最终有1500万~4000万图片，分22000多类。推动目标检测算法发展。

2009年起，ImageNet大规模视觉识别竞赛（ILSVRC）推动基准测试，140万目标图像，1000种类别。2012年AlexNet CNN模型大幅降低错误率，成为里程碑。

近代技术发展

卷积神经网络（CNN）成为图像识别最重要的模型之一。

2010年NEC-UIUC仍用层次结构、检测边缘、不变特征。2012年AlexNet重大突破，7层CNN。2014年GoogLeNet、VGG，2015年微软残差网络ResNet达152层。

CNN早在1998年由Yann LeCun团队发明，用于手写数字识别。结构为输入像素、多层卷积、下采样、全连接。

随着GPU等算力提升，开发出更大更深的CNN模型。数据集创新和算力提升推动模型能力提升。

后续有许多创新CNN结构，帮助模型在更大更深时也能训练和对抗过拟合。

视觉智能探索超越图像识别，如语义分割、知觉分组、3D重构、动作识别、增强现实、虚拟现实等。

如2015CVPR Johnson的「Image Retrieval using Scene Graphs」，视觉基因组数据集不仅框出物体，还描述对象关系、属性、动作等，视觉系统可做丰富任务。

人类可丰富描述场景，结合知识和经验理解图片。典型任务如看图说话（image captioning），以丰富方式理解图片故事，是持续推进的研究领域。

图像分类

图像分类是计算机视觉的核心任务，许多视觉问题（如目标检测、语义分割）都可归结为图像分类。图像分类即：给定一个固定的标签集合，对于输入图像，从中选出一个标签分配给该图像。

挑战

对计算机而言，图像是像素矩阵；对人类，图像包含丰富语义。
存在巨大的语义鸿沟。
例如：输入一张小猫图片，模型需判断其属于${猫, 狗, 帽子, 杯子}$中的哪一类。输入数据为$3$维数组（RGB），如$600\times800\times3=1440000$个数字，每个在$[0,255]$区间。
任务：将这些数字映射为如”猫”这样的标签。

图像分类算法需具备鲁棒性，能适应如下变化：

视角变化（Viewpoint variation）：同一物体多角度展现。
大小变化（Scale variation）：物体可视大小变化。
形变（Deformation）：物体形状可变。
遮挡（Occlusion）：物体部分被遮挡。
光照条件（Illumination conditions）：光照影响像素。
背景干扰（Background clutter）：物体与背景混杂。
类内差异（Intra-class variation）：同类物体外形差异大。
场景物体干扰（Context）：如猫身上有阴影等。

解决方法：采用数据驱动算法——无需手工定义”猫”，只需大量猫图片，模型自动学习。优点：可重用性强。

数据驱动

传统”硬编码”方法：如提取边缘、定义规则（如三线交叉为耳朵），效果差且泛化性差。
数据驱动算法：为每类物体收集大量样例，机器学习归纳规律，生成分类器模型。

过程：

输入：$N$个图像，每个有$K$类标签之一，称为训练集。
学习：用训练集学习每类的模式规律（分类器训练）。
评价：用未见过的图像测试分类器，将预测标签与真实标签对比，评价分类器质量。

范式与模型评估基础

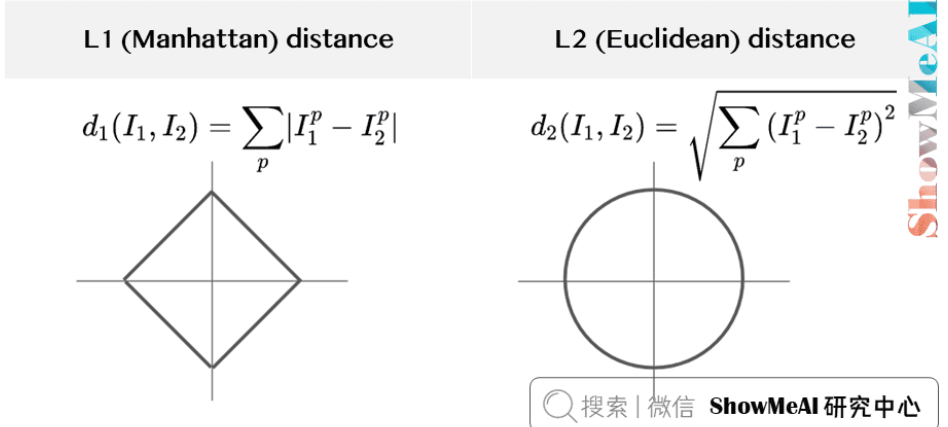
L1 距离（曼哈顿距离）

比较$32\times32\times3$像素块，将两张图片转为向量$I_1$和$I_2$，计算L1距离：

$$
d_1(I_1, I_2) = \sum_p |I_1^p - I_2^p|
$$

$p$为像素点，$I^p$为第$p$个像素值。
L1距离为0表示图片完全相同，差异大则L1值大。

代码示例：

1
2
3

Xtr,Ytr,Xte,Yte=load_CIFAR10('data/cifar10/')
Xtr_rows = Xtr.reshape(Xtr.shape[0],32*32*3)
Xte_rows = Xte.reshape(Xte.shape[0],32*32*3)

Xtr: 训练集图片，Xte: 测试集图片，Ytr/Yte: 标签。
Xtr_rows/Xte_rows: 每张图片展平成3072维行向量。

分类器接口：

train(X, y)：用训练集训练。
predict(X)：预测新数据标签。

Nearest Neighbor分类器实现（L1距离）：

import numpy as np
class NearestNeighbor(object):
    def __init__(self):
        pass
    def train(self, X, y):
        self.Xtr = X
        self.ytr = y
    def predict(self, X):
        num_test = X.shape[0]
        Ypred = np.zeros(num_test, dtype = self.ytr.dtype)
        for i in range(num_test):
            distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
            min_index = np.argmin(distances)
            Ypred[i] = self.ytr[min_index]
        return Ypred

训练复杂度$O(1)$，预测复杂度$O(N)$。
CIFAR-10准确率约$38.6%$。

L2 距离（欧式距离）

公式：
$$
d_2(I_1, I_2) = \sqrt{\sum_p (I_1^p - I_2^p)^2}
$$
代码只需将距离计算改为：

1	distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))

实际可省略sqrt，仅影响数值大小不影响排序。
CIFAR-10准确率约$35.4%$。

L1与L2比较

L1依赖坐标轴，决策边界贴近坐标轴；L2决策边界为圆形。
L2对大差异更敏感，L1对特征敏感。
实践中可都尝试，选效果更好的。

最邻近算法KNN

训练：记住所有训练数据和标签。
预测：与所有训练数据比较，找最接近的标签。
缺点：存储空间大，预测慢。

CIFAR-10数据集

10类，60000张$32\times32$彩色图片，50000训练，10000测试。

KNN改进

KNN思想：找$k$个最近邻，取出现最多的标签作为预测。
$k=1$即最邻近分类器。
$k$大时分类更平滑，对异常值更鲁棒。

KNN核心思想

基于空间距离的特征空间划分。
分类由邻居多数表决决定。

工作原理

有标签的训练集。
输入新数据，与训练集比较，找$k$个最近邻，取最多的标签。
$k$一般不大于20，常用交叉验证选最优$k$。

参数选择

$k$大：模型简单，误差小但近似误差大。
$k$小：对噪声敏感，易过拟合。
二分类常用奇数$k$避免平票。

缺点

对噪声敏感（$k$小），只考虑数量忽略距离（$k$大）。
训练快，预测慢。
高维数据”维度灾难”，需大量训练样本。

超参数调优

$k$和距离度量（L1/L2/点积等）为超参数。
不能用测试集调优，只能用验证集。
常用hold-out法：训练集划分一部分为验证集。
交叉验证法：训练集分多份，轮流做验证。
深度学习一般不用交叉验证，因计算量大。

实际应用建议

数据预处理（清洗、归一化）。
高维数据可降维（如PCA）。
随机分训练/验证集。
在验证集上调优$k$和距离度量。
分类慢可用近似最近邻库（如FLANN）。
记录最优参数，最终只用一次测试集评估。

线性分类：评分函数

线性分类概述

KNN无参数，仅存储数据，$k$为超参数。
参数模型：训练后得到参数，预测时仅用参数，无需训练数据。
线性分类器是最简单的参数模型。

线性分类方法两部分：

评分函数（score function）：原始数据到类别分值的映射。
损失函数（loss function）：量化分数与真实标签一致性，转化为最优化问题，通过更新参数最小化损失。

评分函数

评分函数将像素值映射为各类别得分。
以CIFAR-10为例，$N=50000$，每样本$x_i\in\mathbb{R}^D$，$D=3072$，标签$y_i\in[1,K]$，$K=10$。
定义评分函数：$f: \mathbb{R}^D \to \mathbb{R}^K$，即$D$维输入映射为$K$维分数。
最简单模型：线性模型

$$
f(x_i, W, b) = W x_i + b
$$

$W$为权重矩阵，$b$为偏置项。
$x_i$为$[D\times1]$列向量，$W$为$[K\times D]$，$b$为$[K\times1]$。
输入3072维，输出10维。
训练数据用于学习$W$和$b$，训练后仅需参数即可预测。
只需一次矩阵乘法和加法，预测效率高。

线性分类器理解

$W$是所有分类器的组合：$W$的每一行是一个分类器，对应一个类别。
模板匹配：$W$每行是一个类别模板，分数为输入与模板的内积。
高维空间点：每个类别分数是空间中的线性函数。$W$每行对应一个超平面，偏置$b$决定平移。

没有偏置时，所有超平面都过原点。
线性分类器本质是找到一条直线（或超平面）分隔不同类别。

偏置项和权重合并

可将$W$和$b$合并为一个矩阵，$x_i$增加一维常数1。
新公式：
$$
f(x_i, W) = W x_i
$$
$x_i$为$[3073\times1]$，$W$为$[10\times3073]$，多出一列对应偏置。

图像数据预处理

常对每个特征减去均值（中心化），如每个像素减去训练集均值。
可进一步归一化到$[-1,1]$区间。

线性分类器失效情形

线性分类器只能分隔线性可分数据。
若数据分布无法用一条直线/超平面分开，则线性分类器失效。
典型失效情形：
1. 奇偶分类：类别交替出现，无法用直线分开。
2. 线性不可分：如$1\leq |x|_2 \leq \sqrt{2}$，数据点分布在圆环内，无法用直线分开。
3. 多模型：需多条直线/超平面才能分开。

损失函数与最优化

线性分类：损失函数

概念

定义损失函数（Loss Function）（也叫代价函数 Cost Function 或目标函数 Objective Function）来衡量对预估结果的「不满意程度」。当评分函数输出结果与真实结果之间差异越大，损失函数越大，反之越小。

对于有 $N$ 个训练样本对应 $N$ 个标签的训练集数据 $(x_i, y_i)$，损失函数定义为：

$$
L = \frac{1}{N} \sum_{i=1}^N L_i(f(x_i, W), y_i)
$$

即每个样本损失函数求和取平均。目标就是找到一个合适的 $W$ 使 $L$ 最小。

注意：真正的损失函数 $L$ 还有一项正则损失 $R(W)$，后面会有说明。

多类支持向量机损失

Multiclass SVM Loss

数据损失（data loss）

SVM 的损失函数希望 SVM 在正确分类上的得分始终比不正确分类上的得分高出一个边界值 $\Delta$。

对于第 $i$ 个数据 $(x_i, y_i)$，评分函数 $f(x_i, W)$ 计算不同分类类别的分值，记为 $s$，第 $j$ 个类别的得分为 $s_j$。

多类 SVM 的损失函数定义如下：

$$
L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + \Delta)
$$

直观来看，如果真实标签的分数比其他某个标签的分数高出 $\Delta$，则对该其他标签的损失为 $0$；否则损失就是 $s_j - s_{y_i} + \Delta$。

示例计算：

假设 $y_i = 0, 1, 2$，对于第1张图片「小猫」，评分 $s = [3.2, 5.1, -1.7]$，$s_{y_i} = 3.2$，$\Delta = 1$，则：

$$
L_1 = \max(0, 5.1 - 3.2 + 1) + \max(0, -1.7 - 3.2 + 1) = \max(0, 2.9) + \max(0, -3.9) = 2.9 + 0 = 2.9
$$

同理可得 $L_2 = 0$，$L_3 = 12.9$，整个训练集的损失：

$$
L = \frac{2.9 + 0 + 12.9}{3} = 5.27
$$

合页损失（hinge loss）：

$$
L_i = \sum_{j \neq y_i} \max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta)
$$

其中 $w_j$ 是 $W$ 的第 $j$ 行。

正则化损失（regularization loss）

假设有一组 $W$ 能正确分类所有数据，即所有 $L_i = 0$，但 $W$ 并不唯一。只要任意 $\lambda > 1$，$\lambda W$ 也可以满足 $L_i = 0$。

为此，向损失函数增加正则化惩罚 $R(W)$，常用 L2 范式：

$$
R(W) = \sum_k \sum_l W_{k,l}^2
$$

也可用 L1 范式：

$$
R(W) = \sum_k \sum_l |W_{k,l}|
$$

L1 和 L2 也可组合：

$$
R(W) = \sum_k \sum_l \beta W_{k,l}^2 + |W_{k,l}|
$$

正则化的作用：对大数值权重进行惩罚，提升泛化能力，避免过拟合。通常只对权重 $W$ 正则化，不正则化偏置项 $b$。

多类 SVM 损失完整表达式

$$
L = \underbrace{\frac{1}{N} \sum_{i} L_i}{\text{data loss}} + \underbrace{\lambda R(W)}{\text{regularization loss}}
$$

与二元 SVM 的关系

二元 SVM 损失：

$$
L_i = C \max(0, 1 - y_i w^T x_i) + R(W)
$$

$C$ 与 $\lambda$ 成倒数关系。

Softmax分类器损失

Softmax 分类器是多项式逻辑回归（Multinomial Logistic Regression）。

损失函数

Softmax 函数：

$$
f_k(s) = \frac{e^{s_k}}{\sum_j e^{s_j}}
$$

真实分类标签的概率：

$$
P(Y = y_i | X = x_i) = \frac{e^{s_{y_i}}}{\sum_j e^{s_j}}
$$

损失函数（负对数似然）：

$$
L_i = -\log P(Y = y_i | X = x_i) = -\log \left( \frac{e^{s_{y_i}}}{\sum_j e^{s_j}} \right)
$$

整个数据集的损失：

$$
L = \frac{1}{N} \sum_i \left[ -\log \left( \frac{e^{s_{y_i}}}{\sum_j e^{s_j}} \right) \right] + \lambda R(W)
$$

数值稳定性技巧：

$$
\frac{e^{s_{y_i}}}{\sum_j e^{s_j}} = \frac{e^{s_{y_i} + \log C}}{\sum_j e^{s_j + \log C}}
$$

通常取 $\log C = -\max_j s_j$，即将 $s$ 平移使最大值为0。

Softmax 和 SVM 比较

SVM：鼓励正确类别分值比其他类别高出至少 $\Delta$。
Softmax：鼓励正确分类的归一化对数概率变高，其余变低。
SVM 损失是局部目标化，Softmax 损失永不满足。
Softmax 输出概率分布，但其集中或离散程度由正则化参数 $\lambda$ 决定。

优化

损失函数可视化

损失函数一般定义在高维空间。可通过在1维或2维方向上切片，观察损失函数随参数变化的趋势。

对于单个样本：

$$
L_i = \sum_{j \neq y_i} \left[ \max(0, w_j^T x_i - w_{y_i}^T x_i + 1) \right]
$$

损失函数呈分段线性结构。

优化策略

随机搜索（Random search）

随机尝试不同的 $W$，取损失最小的。

随机本地搜索

从随机 $W$ 开始，生成随机扰动 $aW$，若损失变低则更新。

跟随梯度

计算损失函数的梯度（gradient），沿梯度负方向更新参数。

梯度计算

数值梯度法

利用定义近似计算梯度：

$$
\frac{df(x)}{dx} \approx \frac{f(x + h) - f(x)}{h}
$$

更精确的中心差分公式：

$$
\frac{df(x)}{dx} \approx \frac{f(x + h) - f(x - h)}{2h}
$$

数值梯度法实现简单但效率低，适合梯度检查。

解析梯度法

利用微分公式直接计算梯度，速度快但实现易出错。常与数值梯度法对比进行梯度检查。

以多类 SVM 数据损失为例：

$$
L_i = \sum_{j \neq y_i} \left[ \max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta) \right]
$$

对 $w_{y_i}$ 微分：

$$
\nabla_{w_{y_i}} L_i = - \left( \sum_{j \neq y_i} \mathbb{1}(w_j^T x_i - w_{y_i}^T x_i + \Delta > 0) \right) x_i
$$

对 $w_j$ ($j \neq y_i$) 微分：

$$
\nabla_{w_j} L_i = \mathbb{1}(w_j^T x_i - w_{y_i}^T x_i + \Delta > 0) x_i
$$

梯度下降

Gradient Descent

普通梯度下降

1
2
3

while True:
    weights_grad = evaluate_gradient(loss_fun, data, weights)
    weights += - step_size * weights_grad

小批量梯度下降

Mini-batch gradient descent

每次用小批量（如256个样本）计算梯度并更新参数。

while True:
    data_batch = sample_training_data(data, 256)
    weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
    weights += - step_size * weights_grad

极端情况：每批数据量为1，称为随机梯度下降（SGD）。

小批量大小一般为32、64、128等，通常不需交叉验证调参。

图像特征提取

直接输入原始像素效果不好，可先提取特征（如颜色直方图、词袋、边缘等），神经网络中特征由训练自动获得。

线性分类器可视化程序

线性分类器各种细节可在斯坦福大学开发的在线程序观看演示：点击这里

神经网络与反向传播

反向传播算法

神经网络的训练需要用到梯度下降等方法，核心在于反向传播（Backpropagation），它利用数学中的链式法则递归求解复杂函数的梯度。主流AI工具库（如TensorFlow、PyTorch）最核心的能力之一就是自动微分。

标量形式反向传播

引例

考虑函数
$$
f(x, y, z) = (x + y)z
$$
初值为 $x = -2, y = 5, z = -4$。

将其分解为两部分：

$q = x + y$
$f = qz$

分别计算梯度：

$f$ 对 $q$ 的偏导：$\frac{\partial f}{\partial q} = z = -4$
$f$ 对 $z$ 的偏导：$\frac{\partial f}{\partial z} = q = 3$
$q$ 对 $x$ 的偏导：$\frac{\partial q}{\partial x} = 1$
$q$ 对 $y$ 的偏导：$\frac{\partial q}{\partial y} = 1$

链式法则：
$$
\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \cdot \frac{\partial q}{\partial x} = -4 \cdot 1 = -4 \
\frac{\partial f}{\partial y} = \frac{\partial f}{\partial q} \cdot \frac{\partial q}{\partial y} = -4 \cdot 1 = -4 \
\frac{\partial f}{\partial z} = q = 3
$$

前向传播：从输入到输出计算数值。
反向传播：从输出递归地向前计算梯度。

Python实现：

# 设置输入值
x = -2; y = 5; z = -4

# 前向传播
q = x + y # q = 3
f = q * z # f = -12

# 反向传播
dfdz = q      # df/dz = 3
dfdq = z      # df/dq = -4
dfdx = 1.0 * dfdq # dq/dx = 1, df/dx = -4
dfdy = 1.0 * dfdq # dq/dy = 1, df/dy = -4

直观理解反向传播

每个门单元（如加法、乘法）在前向传播时只需计算自己的输出和局部梯度。
在反向传播时，门单元获得整个网络输出对自己输出的梯度，然后用链式法则乘以自己的局部梯度，得到对输入的梯度，并继续向前传递。

加法门、乘法门和max门

加法门：$f(x, y) = x + y \implies \frac{\partial f}{\partial x} = 1, \frac{\partial f}{\partial y} = 1$
乘法门：$f(x, y) = xy \implies \frac{\partial f}{\partial x} = y, \frac{\partial f}{\partial y} = x$
max门：
$$
f(x, y) = \max(x, y) \
\frac{\partial f}{\partial x} = \mathbb{1}(x \geq y) \
\frac{\partial f}{\partial y} = \mathbb{1}(y \geq x)
$$
加法门是梯度分配器，输入梯度等于输出梯度。
乘法门是梯度转换器，输入梯度等于输出梯度乘以另一个输入值。
max门是梯度路由器，较大输入的梯度等于输出梯度，较小输入的梯度为0。

复杂示例

考虑
$$
f(w, x) = \frac{1}{1 + e^{-(w_0 x_0 + w_1 x_1 + w_2)}}
$$

常用门单元及其导数：

倒数门：$f(x) = \frac{1}{x} \implies \frac{df}{dx} = -\frac{1}{x^2}$
加法门：$f_c(x) = c + x \implies \frac{df}{dx} = 1$
指数门：$f(x) = e^x \implies \frac{df}{dx} = e^x$
乘法门：$f_a(x) = ax \implies \frac{df}{dx} = a$

sigmoid门单元：
$$
\sigma(x) = \frac{1}{1 + e^{-x}} \
\frac{d\sigma(x)}{dx} = (1 - \sigma(x))\sigma(x)
$$

Python实现：

# 假设一些随机数据和权重
w = [2, -3, -3]
x = [-1, -2]

# 前向传播
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid

# 反向传播
ddot = (1 - f) * f
dx = [w[0] * ddot, w[1] * ddot]
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot]

分段计算示例

$$
f(x, y) = \frac{x + \sigma(y)}{\sigma(x) + (x + y)^2}
$$

前向传播：

x = 3
y = -4
sigy = 1.0 / (1 + math.exp(-y))
num = x + sigy
sigx = 1.0 / (1 + math.exp(-x))
xpy = x + y
xpysqr = xpy**2
den = sigx + xpysqr
invden = 1.0 / den
f = num * invden

反向传播：

# 回传 f = num * invden
dnum = invden
dinvden = num
# 回传 invden = 1.0 / den
dden = (-1.0 / (den**2)) * dinvden
# 回传 den = sigx + xpysqr
dsigx = dden
dxpysqr = dden
# 回传 xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr
# 回传 xpy = x + y
dx = dxpy
dy = dxpy
# 回传 sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx
# 回传 num = x + sigy
dx += dnum
dsigy = dnum
# 回传 sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy

注意：

前向传播变量要缓存，反向传播时用到。
变量多次出现时，反向传播要用 += 累加梯度。

多元链式法则：
$$
\frac{\partial f}{\partial x} = \sum_{q_i} \frac{\partial f}{\partial q_i} \frac{\partial q_i}{\partial x}
$$

实际应用

计算图主类结构：

class ComputationalGraph(object):
    def forward(self, inputs):
        for gate in self.graph.nodes_topologically_sorted():
            gate.forward()
        return loss

    def backward(self):
        for gate in reversed(self.graph.nodes_topologically_sorted()):
            gate.backward()
        return inputs_gradients

门单元类示例（乘法门）：

class MultiplyGate(object):
    def forward(self, x, y):
        z = x * y
        self.x = x
        self.y = y
        return z

    def backward(self, dz):
        dx = self.y * dz
        dy = self.x * dz
        return [dx, dy]

向量形式反向传播

考虑如下例子：
$$
f(x, W) = |W x|^2 = \sum_{i=1}^n (W x)_i^2
$$
其中 $x$ 是 $n$ 维向量，$W$ 是 $n \times n$ 矩阵。

设 $q = W x$，则
$$
\frac{\partial f}{\partial q_i} = 2q_i \implies \frac{\partial f}{\partial q} = 2q \
\frac{\partial q_k}{\partial W_{i, j}} = \mathbb{1}{i=k} x_j \implies \frac{\partial f}{\partial W{i, j}} = 2q_i x_j \implies \frac{\partial f}{\partial W} = 2q x^T \
\frac{\partial q_k}{\partial x_i} = W_{k, i} \implies \frac{\partial f}{\partial x_i} = \sum_{k=1}^n 2q_k W_{k, i} \implies \frac{\partial f}{\partial x} = 2W^T q
$$

Python实现：

import numpy as np
W = np.array([[0.1, 0.5], [-0.3, 0.8]])
x = np.array([0.2, 0.4]).reshape((2, 1))
q = W.dot(x)
f = np.sum(np.square(q), axis=0)
dq = 2 * q
dW = dq.dot(x.T)
dx = W.T.dot(dq)

注意：

权重的梯度 $dW$ 的尺寸与 $W$ 一致。
最终损失函数是标量，每个门单元的输入梯度与原输入形状相同。

神经网络简介

神经网络算法介绍

线性分类器：
$$
s = W x
$$
其中 $W$ 是 $[10 \times 3072]$，$x$ 是 $[3072 \times 1]$。

两层神经网络：
$$
s = W_2 \max(0, W_1 x)
$$

$W_1$ 例：$[100 \times 3072]$，将图像转为100维向量。
$\max(0, -)$ 是ReLU激活函数。
$W_2$：$[10 \times 100]$，输出10个分类评分。

注意： 非线性函数是神经网络表达能力的关键。

三层神经网络：
$$
s = W_3 \max(0, W_2 \max(0, W_1 x))
$$

两层神经网络代码示例（中间层用sigmoid）：

import numpy as np
from numpy.random import randn

N, D_in, H, D_out = 64, 1000, 100, 10
x, y = randn(N, D_in), randn(N, D_out)
w1, w2 = randn(D_in, H), randn(H, D_out)

for t in range(10000):
    h = 1 / (1 + np.exp(-x.dot(w1)))
    y_pred = h.dot(w2)
    loss = np.square(y_pred - y).sum()
    print(str(t)+': '+str(loss))

    # 反向传播
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h.T.dot(grad_y_pred)
    grad_h = grad_y_pred.dot(w2.T)
    grad_w1 = x.T.dot(grad_h * h * (1 - h))

    w1 -= 1e-4 * grad_w1
    w2 -= 1e-4 * grad_w2

神经网络与真实神经对比

神经元（neuron）是大脑的基本计算单位。
数学模型：输入信号 $x_0$ 乘以权重 $w_0$，所有输入加权求和后加偏置，经过激活函数 $f$ 输出。

激活函数常用sigmoid：
$$
f(x) = \frac{1}{1 + e^{-x}}
$$

代码示例：

class Neuron:
    def neuron_tick(self, inputs):
        cell_body_sum = np.sum(inputs * self.weights) + self.bias
        firing_rate = 1.0 / (1.0 + np.exp(-cell_body_sum))
        return firing_rate

常用激活函数

Sigmoid: $f(x) = \frac{1}{1 + e^{-x}}$
Tanh: $f(x) = \tanh(x)$
ReLU: $f(x) = \max(0, x)$
Leaky ReLU, ELU, Softplus等

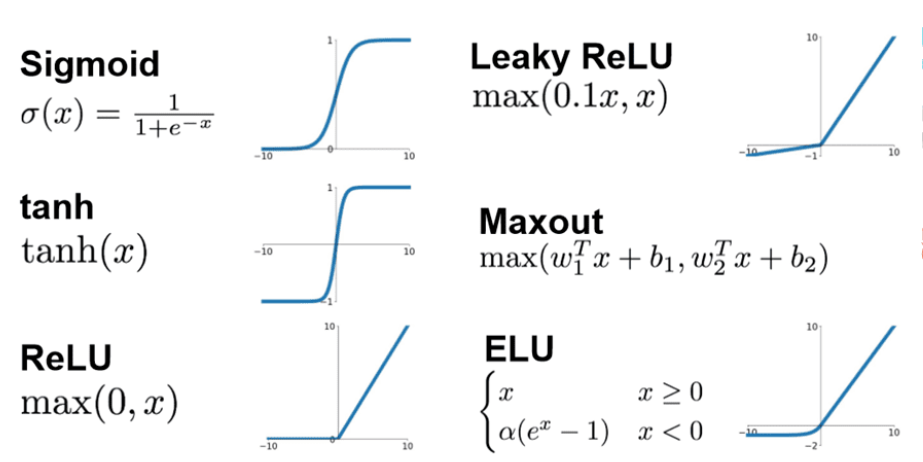
激活函数	函数表达式	值域	零均值	梯度消失	计算成本	稀疏性	神经元死亡	平滑性	主要优点	主要缺点	典型场景
Sigmoid	$\frac{1}{1+e^{-x}}$	(0,1)	❌	✅ 两端饱和	高	❌	❌	✅	平滑、概率解释	梯度消失、非零均值	二分类输出层
Tanh	$\frac{e^x-e^{-x}}{e^x+e^{-x}}$	(-1,1)	✅	✅ 两端饱和	高	❌	❌	✅	零均值、比Sigmoid收敛快	梯度消失	RNN/LSTM内部
ReLU	$ max(0,x)$	[0,+∞)	❌	❌ 正区间不饱和	极低	✅	✅	❌	计算快、缓解梯度消失	神经元死亡	CNN隐藏层
Leaky ReLU	$\max(\alpha x,x),\ \alpha \text{≈0.01}$	(-∞,+∞)	❌	❌	低	✅	❌	❌	解决神经元死亡	α需调参、非零均值	通用替代ReLU

神经网络结构

最常见的结构是全连接层（fully-connected layer），即每层神经元与前后层完全连接，无循环。

$N$层神经网络不计输入层。
参数量 = 权重数 + 偏置数。

例：

2层网络，隐层4个神经元，输出层2个神经元，输入层3个神经元（输入维度）。
- 神经元数：$4+2=6$
- 权重数：$[3 \times 4] + [4 \times 2] = 20$
- 偏置数：$4+2=6$
- 总参数：$26$
3层网络，两个隐层各4个神经元，输出层1个神经元。
- 神经元数：$4+4+1=9$
- 权重数：$[3 \times 4] + [4 \times 4] + [4 \times 1] = 32$
- 偏置数：$4+4+1=9$
- 总参数：$41$

现代卷积神经网络可达上亿参数、上百层。

三层神经网络代码示例

import numpy as np

# 激活函数
f = lambda x: 1.0 / (1.0 + np.exp(-x))

# 随机输入向量3x1
x = np.random.randn(3, 1)
# 权重和偏置
W1, W2, W3 = np.random.randn(4, 3), np.random.randn(4, 4), np.random.randn(1, 4)
b1, b2 = np.random.randn(4, 1), np.random.randn(4, 1)
b3 = 1

# 前向传播
h1 = f(np.dot(W1, x) + b1)
h2 = f(np.dot(W2, h1) + b2)
out = np.dot(W3, h2) + b3

$W_1$：$[4 \times 3]$，$b_1$：$[4 \times 1]$
$W_2$：$[4 \times 4]$，$b_2$：$[4 \times 1]$
$W_3$：$[1 \times 4]$，$b_3$：标量

注意： 最后一层通常无激活函数。

理解神经网络

神经网络定义了一系列函数族，权重为参数。
至少一个隐层的神经网络是通用近似器，可近似任意连续函数。
实践中，3层神经网络优于2层，但继续加深（4、5、6层）提升有限。卷积神经网络则深度越大效果越好。

秋月春风

明月守灯寻长梦，梦长寻灯守月明

明月守灯寻长梦，梦长寻灯守月明

秋月春风

发展历程

历史

近代技术发展

图像分类

挑战

数据驱动

范式与模型评估基础

L1 距离（曼哈顿距离）

L2 距离（欧式距离）

L1与L2比较

最邻近算法KNN

CIFAR-10数据集

KNN改进

KNN核心思想

工作原理

参数选择

缺点

超参数调优

实际应用建议

线性分类：评分函数

线性分类概述

评分函数

线性分类器理解

偏置项和权重合并

图像数据预处理

线性分类器失效情形

损失函数与最优化

线性分类：损失函数

概念

多类支持向量机损失

数据损失（data loss）

正则化损失（regularization loss）

多类 SVM 损失完整表达式

与二元 SVM 的关系

Softmax分类器损失

损失函数

Softmax 和 SVM 比较

优化

损失函数可视化

优化策略

随机搜索（Random search）

随机本地搜索

跟随梯度

梯度计算

数值梯度法

解析梯度法

梯度下降

普通梯度下降

小批量梯度下降

图像特征提取

线性分类器可视化程序

神经网络与反向传播

反向传播算法

标量形式反向传播

引例

直观理解反向传播

加法门、乘法门和max门

复杂示例

分段计算示例

实际应用

向量形式反向传播

神经网络简介

神经网络算法介绍

神经网络与真实神经对比

常用激活函数

神经网络结构

三层神经网络代码示例

理解神经网络