机器学习分类算法

• 参考：https://www.showmeai.tech/

监督学习（Supervised Learning）：训练集有标记信息，学习方式有分类和回归。

监督学习的数学原理

1. 问题定义

• 输入空间：$X \in \mathbb{R}^n$，n维特征向量
• 输出空间：$Y$，回归问题 $Y \in \mathbb{R}$，分类问题 $Y \in {0,1}$
• 训练集：$D = {(x_i, y_i)}{i=1}^N$

2. 损失函数

   • 定义：损失函数用于衡量模型预测值与真实值之间的差距
   • 常见损失函数：
     • 回归问题：
       • 均方误差(MSE)：$L(y, \hat{y}) = \frac{1}{2}(y - \hat{y})^2$
       • 平均绝对误差(MAE)：$L(y, \hat{y}) = |y - \hat{y}|$
     • 分类问题：
       • 对数损失：$L(y, \hat{y}) = -y\log(\hat{y}) - (1-y)\log(1-\hat{y})$
       • 交叉熵损失：$L(y, \hat{y}) = -\sum_{i=1}^C y_i\log(\hat{y}_i)$
   • 特点：
     • 可导性：损失函数需要可导，便于计算梯度
     • 凸性：通常选择凸函数，保证优化过程收敛
     • 可加性：支持样本级别的损失累加

3. 目标函数

   • 总体目标函数：$Obj(\Theta) = L(\Theta) + \Omega(\Theta)$

     • $L(\Theta)$：训练损失函数，衡量模型预测值与真实值的差距
     • $\Omega(\Theta)$：正则化项，控制模型复杂度
     • 同时有这两项的意义：在保证模型预测准确性的同时，控制模型复杂度，防止过拟合

   • 第t次迭代的目标函数：
     $Obj^{(t)} = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t)$

     • $\hat{y}_i^{(t-1)}$：前t-1棵树的预测结果
     • $f_t(x_i)$：第t棵树的预测结果
     • 意义：每次迭代都优化当前树的预测结果，同时考虑模型复杂度

4. 正则化项

   • 树的复杂度定义：
     $\Omega(f_t) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2$
     • $T$：叶子节点个数，控制树的深度
     • $w_j$：第j个叶子节点的权重，控制节点预测值
     • $\gamma, \lambda$：控制正则化强度的超参数
   • 意义：
     • 控制树的生长，防止过拟合
     • 平衡模型的复杂度和预测能力
     • 提高模型的泛化能力

逻辑回归

逻辑回归是一种用于分类的监督学习算法，尽管名称中有”回归”二字，但它主要用于解决分类问题。逻辑回归基于逻辑函数（即Sigmoid函数）将线性回归的输出映射到(0,1)区间，表示事件发生的概率。

原理

逻辑回归的模型可以表示为：$P(y=1∣x)=σ(β_0+β_1x_1+β_2x_2+⋯+β_nx_n)$，其中，σ(z)= $\frac{1}{1+e^{-z}}$ 是Sigmoid函数，将线性组合的输出映射到(0,1)区间，表示事件发生的概率。逻辑回归通过最大似然估计来估计模型参数，目标是找到一组参数 β ，使得模型对训练数据的预测概率与实际结果尽可能一致。

损失函数

逻辑回归的损失函数采用对数似然损失函数（Log Loss），其表达式为：$J(β)=- \frac{1}{m} ∑_{i=1}^m [y_i ln(\hat{y}_i)+(1−y_i)ln(1−\hat{y}_i)]$，其中，m 是样本数量，$y_i$ 是真实标签（0或1），$\hat{y}_i =P(y=1∣x_i)$ 是模型预测的概率。通过最小化这个损失函数，可以得到最优的模型参数 β。

核心思想

逻辑回归是线性回归的一种扩展，用来处理分类问题。其核心思想是：

1. 先用线性函数拟合数据
2. 通过Sigmoid函数将线性输出压缩到(0,1)区间
3. 将压缩后的值解释为概率

• 线性回归：输出连续值，无法限定范围
• 逻辑回归：通过Sigmoid函数将输出映射到(0,1)区间
• Sigmoid函数：$σ(z) = \frac{1}{1+e^{-z}}$
  • 输出范围：(0,1)
  • 当z趋近于正无穷时，σ(z)趋近于1
  • 当z趋近于负无穷时，σ(z)趋近于0
  • 当z=0时，σ(z)=0.5

决策边界

决策边界是分类器对样本进行区分的边界，分为：

1. 线性决策边界：

   • 形式：$θ_0 + θ_1x_1 + θ_2x_2 = 0$
   • 特点：直线或超平面
   • 适用：线性可分数据

2. 非线性决策边界：

   • 形式：通过多项式特征实现
   • 特点：曲线或曲面
   • 适用：线性不可分数据

特点

• 输出结果为概率值：逻辑回归的输出是一个概率值，表示样本属于正类的概率。
• 适用于二分类问题：逻辑回归主要用于解决二分类问题。
• 对数据分布要求相对宽松：不假设自变量和因变量之间具有线性关系，也不要求残差服从正态分布。
• 模型的可解释性强：模型的参数具有明确的统计意义。

优点

• 简单易懂：模型结构相对简单，易于理解和实现。
• 计算效率高：训练过程通常采用梯度下降法或其变种，计算效率高。
• 可解释性强：参数具有明确的统计意义，可直观地解释每个自变量对目标变量的影响。
• 适用于高维数据：对高维数据具有较好的适应性。

缺点

• 仅适用于线性可分问题：本质上是一种线性分类模型，对非线性问题分类性能可能较差。
• 易受多重共线性影响：自变量之间存在严重的多重共线性时，参数估计可能会变得不稳定。
• 对异常值敏感：异常值可能会对模型的参数估计产生较大影响。
• 无法处理复杂的特征交互：默认不考虑特征之间的交互作用。

模型优化

• 特征工程：特征选择、特征构造、特征缩放、处理缺失值等。
• 正则化：L1正则化、L2正则化、弹性网络正则化等。
• 优化算法：梯度下降法、牛顿法、拟牛顿法等。
• 模型评估与选择：评估指标包括准确率、精确率、召回率、F1分数、ROC曲线和AUC值等，交叉验证方法如k折交叉验证、留一法交叉验证等。

正则化

1. L2正则化：

   • 形式：$J(θ) = J(θ) + \frac{λ}{2m}\sum_{j=1}^nθ_j^2$
   • 作用：限制参数大小
   • 效果：防止过拟合

2. L1正则化：

   • 形式：$J(θ) = J(θ) + \frac{λ}{m}\sum_{j=1}^n|θ_j|$
   • 作用：产生稀疏解
   • 效果：特征选择

特征工程

1. 多项式特征：

   • 增加特征维度
   • 捕捉特征间关系
   • 实现非线性切分

2. 特征变换：

   • 标准化
   • 归一化
   • 特征选择

梯度下降优化

1. 梯度下降原理：

   • 向函数梯度反方向迭代
   • 逐步减小损失函数值
   • 最终找到最优参数

2. 学习率选择：

   • 太大：可能错过最优解
   • 太小：收敛速度慢
   • 需要根据具体问题调整

代码实现

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
import numpy as np
import pandas as pd

# 数据预处理
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 添加多项式特征
poly = PolynomialFeatures(degree=2, include_bias=False)
X_train_poly = poly.fit_transform(X_train_scaled)
X_test_poly = poly.transform(X_test_scaled)

# 创建逻辑回归模型实例
model = LogisticRegression(
    penalty='l2',           # 正则化类型：'l1'或'l2'
    C=1.0,                  # 正则化强度的倒数
    solver='liblinear',     # 优化算法
    max_iter=1000,          # 最大迭代次数
    random_state=42
)

# 在训练集上训练模型
model.fit(X_train_poly, y_train)

# 在测试集上进行预测
y_pred = model.predict(X_test_poly)
y_pred_proba = model.predict_proba(X_test_poly)[:, 1]

# 计算评估指标
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
roc_auc = roc_auc_score(y_test, y_pred_proba)

# 输出模型参数
print("模型参数：", model.coef_)
print("截距：", model.intercept_)
print("准确率：", accuracy)
print("精确率：", precision)
print("召回率：", recall)
print("F1分数：", f1)
print("ROC AUC：", roc_auc)

K近邻算法

K近邻算法（K-Nearest Neighbors，KNN）是一种基本的分类和回归方法。它的核心思想是：一个样本的类别由它最接近的K个邻居（K为正整数，通常较小）的多数类别决定。

原理

K近邻居法采用向量空间模型来分类(本质是划分特征空间)，概念为相同类别的案例，彼此的相似度高。而可以借由计算与已知类别案例之相似度，来评估未知类别案例可能的分类。

KNN算法的工作原理是：

1. 存在一个样本数据集合（训练集），每个数据都有标签
2. 输入没有标签的新数据后，将新数据的每个特征与训练集中数据对应的特征进行比较
3. 提取训练集中特征最相似数据（最近邻）的分类标签
4. 选择K个最相似数据中出现次数最多的分类，作为新数据的分类

核心要素

1. 距离度量准则

   • 曼哈顿距离（L1距离）：

     • 公式：$d(x,y) = \sum_{i=1}^n |x_i - y_i|$
     • 特点：计算速度快，对异常值不敏感
     • 适用：特征差异较大时

   • 欧氏距离（L2距离）：

     • 公式：$d(x,y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}$
     • 特点：最常用的距离度量方式
     • 适用：特征差异较小时

   • 切比雪夫距离：

     • 公式：$d(x,y) = \max_{i=1}^n |x_i - y_i|$
     • 特点：只考虑最大维度差异
     • 适用：特征差异显著时

2. K值的选择

   • K值较小：

     • 模型复杂，容易过拟合
     • 易受噪声影响
     • 决策边界更复杂
     • 适合：数据噪声小，类别边界清晰

   • K值较大：

     • 模型简单，可能欠拟合
     • 能够减小噪声的影响
     • 类别之间的界限变得模糊
     • 适合：数据噪声大，类别边界模糊

   • 选择方法：

     • 交叉验证
     • 网格搜索
     • 经验法则：K通常取奇数，避免平票
     • 一般K值不超过训练样本数的平方根

特点

优点

• 精度高：

  • 理论成熟，思想简单
  • 基于实例的学习，不需要训练过程
  • 对数据分布没有假设

• 对异常值不敏感：

  • 基于距离度量，对异常值有较好的鲁棒性
  • 通过K个邻居投票，减少单个异常值的影响

• 无数据输入假定：

  • 不需要对数据分布做假设
  • 适用于各种类型的数据

• 可用于分类和回归：

  • 分类：通过投票实现
  • 回归：通过平均实现

缺点

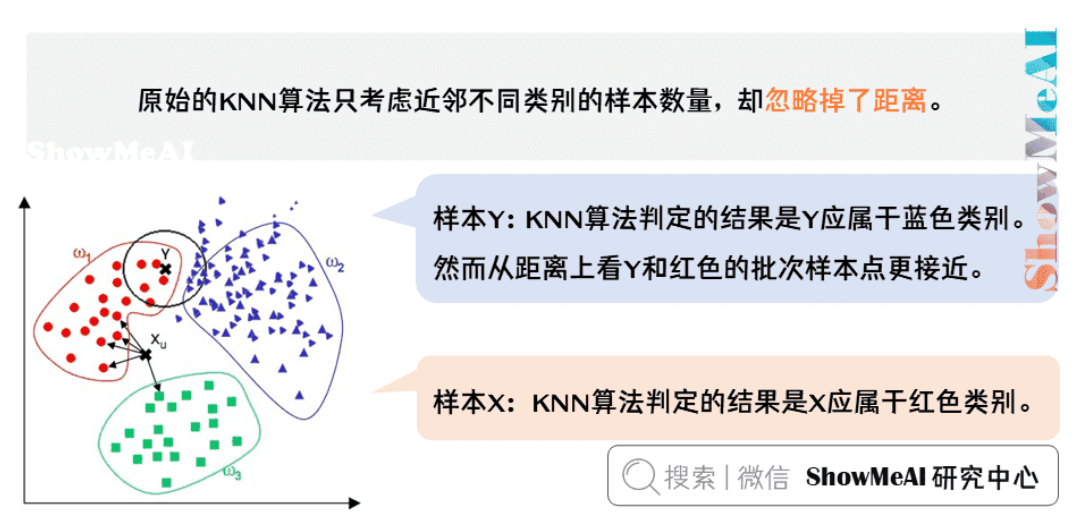
• 对噪声数据过于敏感：

  • 当不同类别的样本距离相等时，无法准确判断
  • 例如：一个蓝点和两个红点到绿点的距离相等，无法确定绿点的类别

• 计算复杂度高：

  • 需要计算待分类样本与所有训练样本的距离
  • 时间复杂度：O(n)，n为训练样本数
  • 预测时间随训练集增大而线性增长

• 空间复杂度高：

  • 需要存储所有训练样本
  • 空间复杂度：O(n)，n为训练样本数
  • 对大规模数据集不友好

• 样本库容量依赖性：

  • 对训练样本数量和质量要求较高
  • 需要足够的样本覆盖特征空间
  • 样本分布不均匀时效果差

模型优化

1. 距离度量优化

   • 特征标准化：

     • 消除特征尺度差异
     • 使用Z-score标准化
     • 使用Min-Max归一化

   • 特征权重调整：

     • 根据特征重要性赋予权重
     • 使用互信息选择特征
     • 使用特征选择算法

   • 距离度量方式选择：

     • 根据数据特点选择合适距离度量
     • 可以自定义距离度量函数
     • 考虑特征之间的相关性

2. 样本库优化

   • 样本编辑：

     • 删除冗余样本
     • 删除噪声样本
     • 保留边界样本

   • 样本压缩：

     • 保留代表性样本
     • 使用聚类中心
     • 使用原型选择

   • 样本维护：

     • 动态更新样本库
     • 增量学习
     • 在线学习

3. 搜索优化

   • KD树：

     • 将特征空间划分为超矩形区域
     • 减少距离计算次数
     • 适合低维数据

   • 球树：

     • 将特征空间划分为超球体
     • 比KD树更高效
     • 适合高维数据

   • 局部敏感哈希：

     • 将相似样本映射到相同桶
     • 快速找到近邻
     • 适合大规模数据

代码实现

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd

# 创建KNN分类器实例
model = KNeighborsClassifier(
    n_neighbors=5,           # K值
    weights='uniform',       # 权重：'uniform'或'distance'
    metric='minkowski',      # 距离度量方式
    p=2,                     # 距离度量参数：1为曼哈顿距离，2为欧氏距离
    algorithm='auto'         # 搜索算法：'auto', 'ball_tree', 'kd_tree', 'brute'
)

# 使用网格搜索找到最优参数
param_grid = {
    'n_neighbors': [3, 5, 7, 9],
    'weights': ['uniform', 'distance'],
    'metric': ['minkowski'],
    'p': [1, 2]
}
grid_search = GridSearchCV(model, param_grid, cv=5)
grid_search.fit(X_train_scaled, y_train)

# 使用最优参数训练模型
best_model = grid_search.best_estimator_
best_model.fit(X_train_scaled, y_train)

# 在测试集上进行预测
y_pred = best_model.predict(X_test_scaled)

# 计算评估指标
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)

朴素贝叶斯

朴素贝叶斯是一种基于贝叶斯定理的分类算法。”朴素”的意思是假设特征之间相互独立。与其他分类算法（如KNN、逻辑回归、决策树等）不同，朴素贝叶斯是一种生成方法，它直接学习特征和类别的联合分布，而不是直接学习决策函数或条件分布。

原理

朴素贝叶斯算法的核心思想是通过考虑特征概率来预测分类。对于给定的待分类样本，计算在此样本出现的条件下各个类别出现的概率，选择概率最大的类别作为预测结果。

贝叶斯公式

朴素贝叶斯基于贝叶斯定理：
$P(y|x) = \frac{P(x|y)P(y)}{P(x)}$

其中：

• $P(y|x)$ 是后验概率，表示在特征x出现的条件下类别y的概率
• $P(x|y)$ 是似然概率，表示在类别y的条件下特征x出现的概率
• $P(y)$ 是先验概率，表示类别y的概率
• $P(x)$ 是特征x的概率

条件独立假设

朴素贝叶斯假设所有特征之间相互独立，因此：
$P(x|y) = P(x_1|y)P(x_2|y)…P(x_n|y)$

分类决策

对于给定的样本x，计算每个类别y的后验概率：
$P(y|x) = \frac{P(x|y)P(y)}{P(x)} = \frac{P(y)\prod_{i=1}^n P(x_i|y)}{P(x)}$

由于$P(x)$对所有类别都是相同的，因此可以简化为：
$P(y|x) \propto P(y)\prod_{i=1}^n P(x_i|y)$

最终选择后验概率最大的类别作为预测结果：
$y^* = \arg\max_y P(y|x)$

核心要素

1. 先验概率与后验概率

   • 先验概率：事件发生前的预判概率

     • 基于历史数据统计：例如，在垃圾邮件分类中，根据历史数据统计垃圾邮件占总邮件的比例
       • 公式：$P(y) = \frac{N_y}{N}$，其中$N_y$是类别y的样本数，$N$是总样本数
     • 基于背景常识：例如，在疾病诊断中，根据人群患病率估计
       • 公式：$P(y) = \frac{\text{患病人数}}{\text{总人数}}$
     • 基于主观观点：例如，在风险评估中，根据专家经验判断
       • 公式：$P(y) = \text{专家评估概率}$

   • 后验概率：事件发生后的反向条件概率

     • 基于先验概率求得：通过贝叶斯公式计算
       • 公式：$P(y|x) = \frac{P(x|y)P(y)}{P(x)}$
     • 用于最终分类决策：选择后验概率最大的类别
       • 公式：$y^* = \arg\max_y P(y|x)$

2. 条件概率计算

   • 离散特征：

     • 多项式朴素贝叶斯：

       • 适用于文本分类
       • 考虑词频信息
       • 例如：在垃圾邮件分类中，统计每个词在垃圾邮件和正常邮件中出现的频率
       • 公式：$P(x_i|y) = \frac{N_{yi} + \alpha}{N_y + \alpha N}$，其中$N_{yi}$是特征$x_i$在类别y中出现的次数，$N_y$是类别y的样本数，$\alpha$是平滑参数

     • 伯努利朴素贝叶斯：

       • 适用于二值特征
       • 只考虑特征是否出现
       • 例如：在文本分类中，只考虑词是否出现，不考虑出现次数
       • 公式：$P(x_i|y) = \frac{N_{yi} + \alpha}{N_y + 2\alpha}$，其中$N_{yi}$是特征$x_i$在类别y中出现的样本数

   • 连续特征：

     • 高斯朴素贝叶斯：
       • 假设特征服从正态分布
       • 需要计算均值和方差
       • 例如：在身高预测中，假设身高服从正态分布，计算不同类别的身高均值和方差
       • 公式：$P(x_i|y) = \frac{1}{\sqrt{2\pi\sigma_{yi}^2}} \exp\left(-\frac{(x_i - \mu_{yi})^2}{2\sigma_{yi}^2}\right)$，其中$\mu_{yi}$和$\sigma_{yi}^2$分别是类别y下特征$x_i$的均值和方差

特点

优点

• 简单高效：

  • 训练和预测速度快：时间复杂度为O(n)，n为特征数
  • 实现简单：只需要计算概率，不需要复杂的优化
  • 内存占用小：只需要存储概率表

• 对小规模数据表现好：

  • 能处理多分类问题：可以计算多个类别的概率
  • 对缺失数据不敏感：可以通过概率计算处理缺失值
  • 适合增量学习：可以动态更新概率表

• 理论基础扎实：

  • 基于概率论：有严格的数学推导
  • 可解释性强：可以解释每个特征对分类的贡献
  • 预测结果有概率意义：可以给出分类的置信度

缺点

• 特征独立性假设：

  • 实际中特征往往相关：例如，在文本分类中，某些词经常一起出现
  • 可能影响分类效果：当特征相关性强时，分类效果会下降
  • 需要特征选择：去除相关特征，提高独立性

• 对输入数据敏感：

  • 需要特征预处理：标准化、归一化等
  • 对异常值敏感：异常值会影响概率计算
  • 需要处理零概率问题：使用平滑技术

模型优化

平滑处理

原因：使用朴素贝叶斯，有时候会面临零概率问题。

• 在计算实例的概率时，如果某个量在观察样本库（训练集）中没有出现过，会导致整个实例的概率结果是0。

• eg：在文本分类的问题中，当「一个词语没有在训练样本中出现」时，这个词基于公式统计计算得到的条件概率为 0，使用连乘计算文本出现概率时也为 。这是不合理的，不能因为一个事件没有观察到就武断的认为该事件的概率是 0。

• 拉普拉斯平滑：

  • 解决零概率问题：当某个特征在某个类别中没有出现时，概率为0
  • 公式：$P(x_i|y) = \frac{N_{yi} + \alpha}{N_y + \alpha N}$，其中$\alpha$是平滑参数
  • $\alpha$为平滑参数：通常取1，可以根据实际情况调整
  • 例如：在文本分类中，当某个词在某个类别中没有出现时，使用平滑后的概率

特征工程

• 特征选择：

  • 去除无关特征：使用信息增益、卡方检验等方法
    • 信息增益：$IG(x_i) = H(y) - H(y|x_i)$，其中$H(y)$是类别熵，$H(y|x_i)$是条件熵
    • 卡方检验：$\chi^2(x_i) = \sum_{y} \frac{(O_{yi} - E_{yi})^2}{E_{yi}}$，其中$O_{yi}$是观察值，$E_{yi}$是期望值
  • 选择重要特征：保留对分类贡献大的特征
  • 降低特征维度：使用PCA、LDA等方法

• 特征转换：

  • 离散化连续特征：将连续特征转换为离散特征
  • 标准化特征值：使特征值在相同尺度上
    • 公式：$x_i’ = \frac{x_i - \mu_i}{\sigma_i}$，其中$\mu_i$和$\sigma_i$分别是特征$x_i$的均值和标准差
  • 处理缺失值：使用均值、中位数等填充

模型选择

• 多项式模型：

  • 适用于文本分类：考虑词频信息
  • 适合长文本：可以处理大量特征
  • 例如：垃圾邮件分类、新闻分类等

• 伯努利模型：

  • 适用于短文本：只考虑词是否出现
  • 适合二值特征：特征只有0和1两种取值
  • 例如：情感分析、主题分类等

• 高斯模型：

  • 适用于连续特征：假设特征服从正态分布
  • 需要计算均值和方差：对每个类别的每个特征计算
  • 例如：身高预测、体重预测等

代码实现

from sklearn.naive_bayes import MultinomialNB, GaussianNB, BernoulliNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd

# 数据预处理
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 创建朴素贝叶斯模型实例
# 对于文本分类，使用MultinomialNB
model = MultinomialNB(alpha=1.0)  # alpha为平滑参数

# 对于连续特征，使用GaussianNB
# model = GaussianNB()

# 对于二值特征，使用BernoulliNB
# model = BernoulliNB(alpha=1.0)

# 在训练集上训练模型
model.fit(X_train_scaled, y_train)

# 在测试集上进行预测
y_pred = model.predict(X_test_scaled)
y_pred_proba = model.predict_proba(X_test_scaled)

# 计算评估指标
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='weighted')
recall = recall_score(y_test, y_pred, average='weighted')
f1 = f1_score(y_test, y_pred, average='weighted')

# 输出模型参数和评估结果
print("模型参数：", model.class_prior_)  # 先验概率
print("特征对数概率：", model.feature_log_prob_)  # 条件概率
print("准确率：", accuracy)
print("精确率：", precision)
print("召回率：", recall)
print("F1分数：", f1)

# 特征重要性分析
feature_importance = np.abs(model.feature_log_prob_[1] - model.feature_log_prob_[0])
sorted_idx = np.argsort(feature_importance)
print("最重要的特征：", sorted_idx[-5:])  # 输出最重要的5个特征

支持向量机

支持向量机(Support Vector Machine, SVM)是一种强大的监督学习算法，主要用于分类和回归问题。它的核心思想是在特征空间中找到一个最优的超平面，使得不同类别的样本被最大间隔分开。

分类

支持向量机学习方法，针对不同的情况，有由简至繁的不同模型：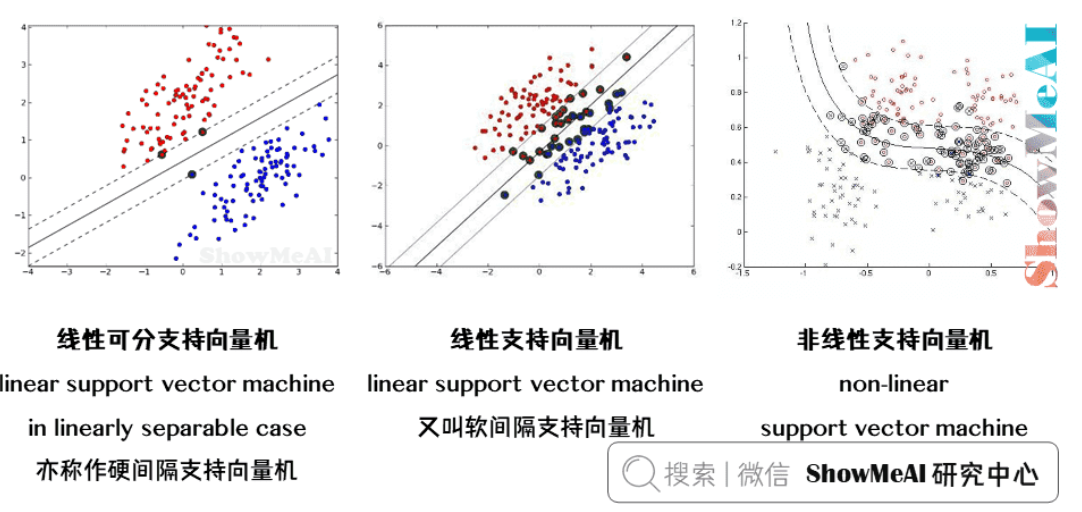

线性可分支持向量机

linear support vector machine in linearly separable case
训练数据线性可分的情况下，通过硬间隔最大化（hard margin maximization），学习一个线性的分类器，即线性可分支持向量机（亦称作硬间隔支持向量机）。

线性支持向量机

linear support vector machine
训练数据近似线性可分的情况下，通过软间隔最大化（soft margin maximization），学习一个线性的分类器，称作线性支持向量机（又叫软间隔支持向量机）。

非线性支持向量机

non-linear support vector machine
训练数据线性不可分的情况下，通过使用核技巧（kernel trick）及软间隔最大化，学习非线性分类器，称作非线性支持向量机。

原理

SVM的基本原理是通过寻找一个最优的超平面来划分不同类别的样本。这个超平面不仅要能够正确分类样本，还要使得不同类别之间的间隔最大化。

最大间隔分类器

1. 分类问题与线性模型

   • 分类问题是监督学习的核心问题之一
   • 当输出变量取有限个离散值时，预测问题便成为分类问题
   • 分类问题的数学本质是空间划分，寻找不同类别的决策边界
   • 对于二分类问题，目标是找到一个超平面$w \cdot x + b = 0$，使得：
     • 对于正类样本：$w \cdot x + b > 0$
     • 对于负类样本：$w \cdot x + b < 0$

2. 最大间隔原则

   • SVM不仅希望把两类样本点区分开，还希望找到鲁棒性最高、稳定性最好的决策边界
   • 决策边界与两侧”最近”的数据点有着”最大”的距离
   • 这样的决策边界具有最强的容错性，不容易受到噪声数据的干扰
   • 支持向量：距离决策边界最近的样本点，它们决定了决策边界的位置

硬间隔最大化

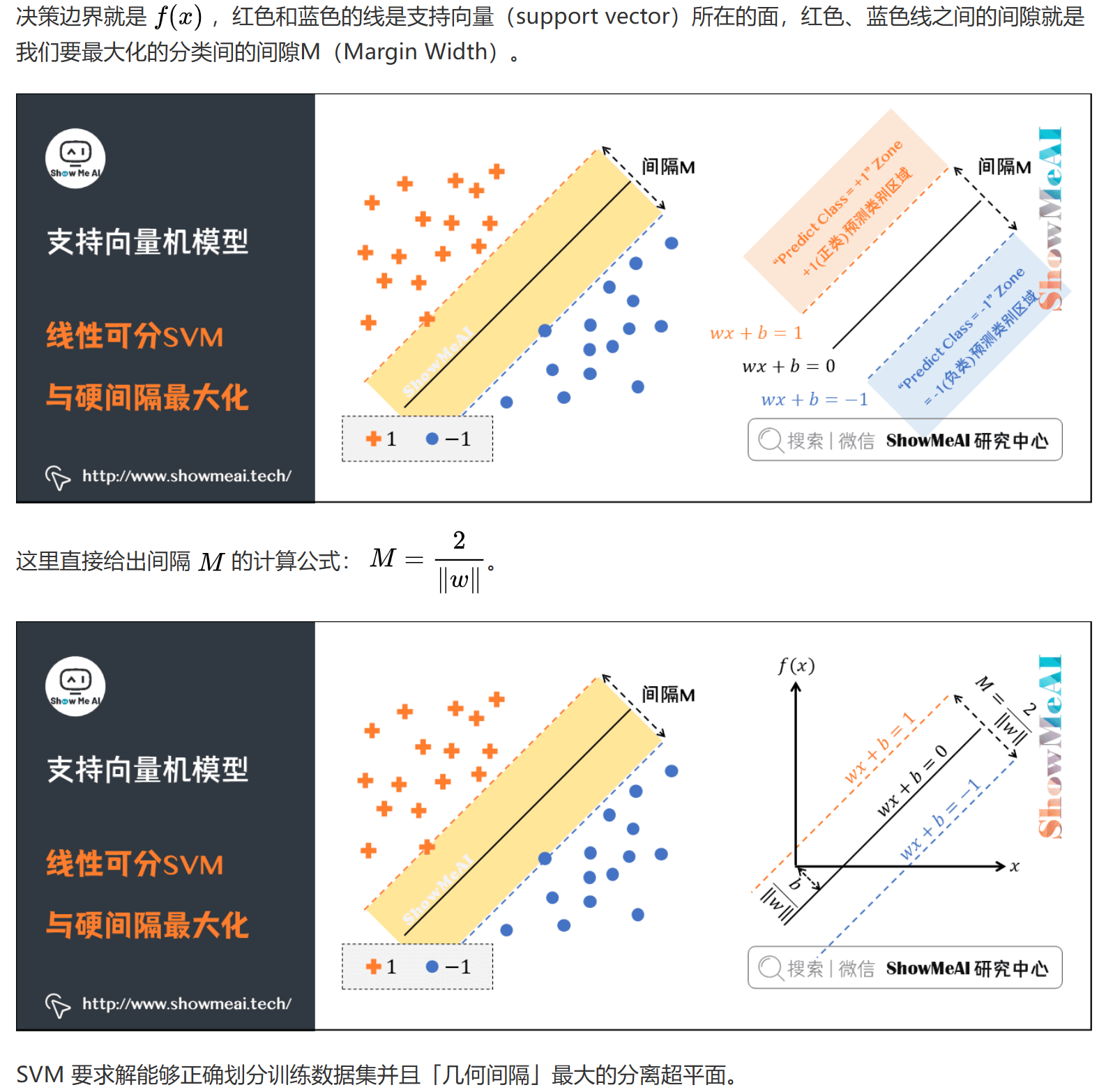
1. 几何间隔

   • 对于给定的数据集$T = {(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}$和超平面$(w,b)$
   • 定义超平面关于样本点$(x_i,y_i)$的几何间隔为：
     $\gamma_i = y_i(\frac{w}{||w||} \cdot x_i + \frac{b}{||w||})$
   • 超平面关于所有样本点的几何间隔的最小值为：
     $\gamma = \min_{i=1,…,N} \gamma_i$
   • 函数间隔：$\hat{\gamma}_i = y_i(w \cdot x_i + b)$
   • 几何间隔与函数间隔的关系：$\gamma_i = \frac{\hat{\gamma}_i}{||w||}$

2. 最优化问题

   • 目标函数：$\max_{w,b} \gamma$
   • 约束条件：$y_i(w \cdot x_i + b) \geq \gamma, i=1,2,…,N$
   • 等价于：$\min_{w,b} \frac{1}{2}||w||^2$
   • 约束条件：$y_i(w \cdot x_i + b) \geq 1, i=1,2,…,N$
   • 拉格朗日函数：
     $L(w,b,\alpha) = \frac{1}{2}||w||^2 - \sum_{i=1}^N \alpha_i[y_i(w \cdot x_i + b) - 1]$
   • KKT条件：
     • $\nabla_w L(w,b,\alpha) = w - \sum_{i=1}^N \alpha_i y_i x_i = 0$
     • $\nabla_b L(w,b,\alpha) = -\sum_{i=1}^N \alpha_i y_i = 0$
     • $\alpha_i \geq 0, i=1,2,…,N$
     • $y_i(w \cdot x_i + b) - 1 \geq 0, i=1,2,…,N$
     • $\alpha_i[y_i(w \cdot x_i + b) - 1] = 0, i=1,2,…,N$

3. 对偶算法

   • 对于给定得线性可分训练数据集，可以首先求对偶问题的解 $\alpha^\star$ ；再利用公式求得原始问题的解 $w^\star$、$b^\star$ ；从而得到分离超平面及分类决策函数。这种算法称为线性可分支持向量机的对偶学习算法，是线性可分支持向量机学习的基本算法。
   • 构建拉格朗日函数：
     $L(w,b,\alpha) = \frac{1}{2}||w||^2 - \sum_{i=1}^N \alpha_i[y_i(w \cdot x_i + b) - 1]$
   • 对偶问题：
     $\max_{\alpha} \sum_{i=1}^N \alpha_i - \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_jy_iy_j(x_i \cdot x_j)$
   • 约束条件：
     • $\sum_{i=1}^N \alpha_iy_i = 0$
     • $\alpha_i \geq 0, i=1,2,…,N$
   • 最优解：
     • $w^\star = \sum_{i=1}^N \alpha_i^\star y_ix_i$
     • $b^\star = y_j - \sum_{i=1}^N \alpha_i^\star y_i(x_i \cdot x_j)$ 其中$j$是满足 $0 < \alpha_j^\star < C$ 的任意下标

软间隔最大化

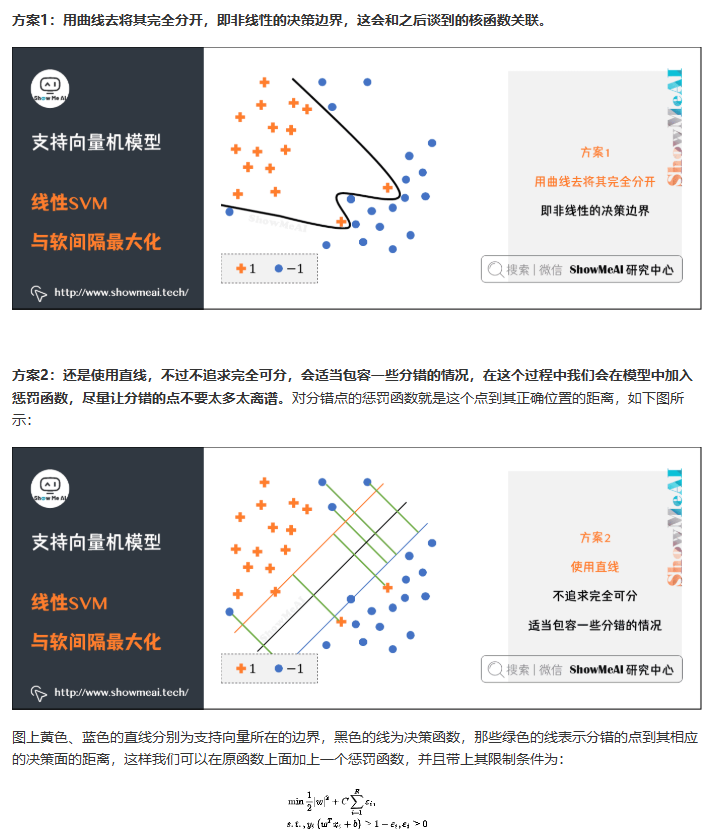
1. 软间隔

   • 引入松弛变量$\xi_i \geq 0$
   • 目标函数：$\min_{w,b,\xi} \frac{1}{2}||w||^2 + C\sum_{i=1}^N \xi_i$
   • 约束条件：
     • $y_i(w \cdot x_i + b) \geq 1 - \xi_i, i=1,2,…,N$
     • $\xi_i \geq 0, i=1,2,…,N$
   • 拉格朗日函数：
     $L(w,b,\xi,\alpha,\mu) = \frac{1}{2}||w||^2 + C\sum_{i=1}^N \xi_i - \sum_{i=1}^N \alpha_i[y_i(w \cdot x_i + b) - 1 + \xi_i] - \sum_{i=1}^N \mu_i\xi_i$
   • KKT条件：
     • $\nabla_w L = w - \sum_{i=1}^N \alpha_i y_i x_i = 0$
     • $\nabla_b L = -\sum_{i=1}^N \alpha_i y_i = 0$
     • $\nabla_{\xi_i} L = C - \alpha_i - \mu_i = 0$
     • $\alpha_i \geq 0, \mu_i \geq 0, i=1,2,…,N$
     • $y_i(w \cdot x_i + b) - 1 + \xi_i \geq 0, i=1,2,…,N$
     • $\alpha_i[y_i(w \cdot x_i + b) - 1 + \xi_i] = 0, i=1,2,…,N$
     • $\mu_i\xi_i = 0, i=1,2,…,N$

2. 惩罚参数C

   • C值越大，对误分类的惩罚越大
   • C值越小，对误分类的惩罚越小
   • 需要根据具体问题选择合适的C值
   • 当$C \to \infty$时，软间隔SVM退化为硬间隔SVM
   • 当$C \to 0$时，允许更多的误分类，决策边界更简单

核函数与核技巧

支持向量机可以借助核技巧完成复杂场景下的非线性分类，当输入空间为欧式空间或离散集合、特征空间为希尔贝特空间时，核函数（kernel function） 表示将输入从输入空间映射到特征空间得到的特征向量之间的内积。
核技巧：通过使用核函数可以学习非线性支持向量机，等价于隐式地在高维的特征空间中学习线性支持向量机。

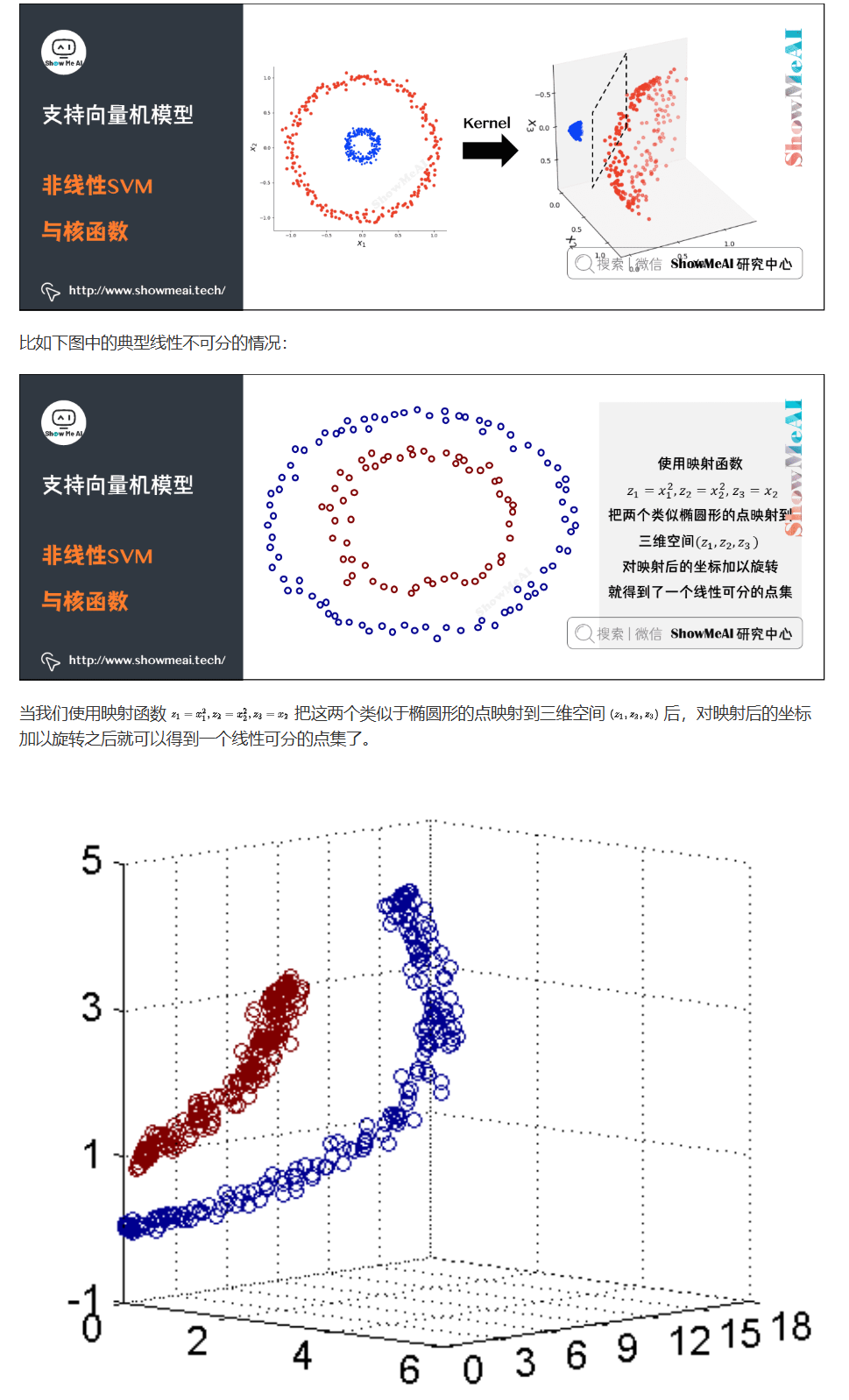
1. 核技巧

   • 将样本从原始空间映射到更高维的特征空间
   • 在特征空间中寻找线性可分的超平面
   • 通过核函数计算特征空间中的内积
   • 映射函数：$\phi: \mathcal{X} \to \mathcal{H}$
   • 核函数：$K(x,y) = \phi(x) \cdot \phi(y)$

2. 常用核函数

   • 线性核：$K(x,y) = x \cdot y$
   • 多项式核：$K(x,y) = (x \cdot y + 1)^d$，其中$d$是多项式的阶数
   • 高斯核：$K(x,y) = \exp(-\frac{||x-y||^2}{2\sigma^2})$，其中$\sigma$是高斯核的带宽
   • Sigmoid核：$K(x,y) = \tanh(\beta x \cdot y + \theta)$，其中$\beta$和$\theta$是参数
   • 拉普拉斯核：$K(x,y) = \exp(-\frac{||x-y||}{\sigma})$，其中$\sigma$是参数
   • 卡方核：$K(x,y) = \exp(-\gamma \sum_{i=1}^n \frac{(x_i-y_i)^2}{x_i+y_i})$，其中$\gamma$是参数

3. 核函数选择

   • 线性核：适用于线性可分的数据
   • 多项式核：适用于图像处理等需要高阶特征的问题
   • 高斯核：适用于大多数非线性问题，是最常用的核函数
   • Sigmoid核：适用于神经网络相关的问题
   • 核函数的选择需要考虑：
     • 数据的特征和分布
     • 计算复杂度
     • 模型的泛化能力

特点

优点

• 全局最优解：SVM是一个凸优化问题，求得的解一定是全局最优解
• 非线性分类：通过核技巧可以处理非线性分类问题
• 高维空间：在高维空间中表现良好，即使特征数量大于样本数量
• 泛化能力强：决策边界只由支持向量决定，具有很好的泛化能力
• 鲁棒性好：对噪声数据具有较强的鲁棒性
• 理论基础扎实：基于统计学习理论，有严格的数学推导
• 可解释性强：决策边界由支持向量决定，易于理解和解释

缺点

• 计算复杂度高：训练时间随样本数量增长而快速增长，时间复杂度为$O(n^2)$
• 内存消耗大：需要存储核矩阵，内存消耗为$O(n^2)$
• 参数选择敏感：对核函数的选择和参数设置比较敏感
• 不适用于大规模数据集：当样本数量很大时，训练时间会变得很长
• 对缺失数据敏感：需要完整的数据集进行训练
• 多分类问题复杂：需要额外的策略来处理多分类问题
• 特征工程要求高：对特征的选择和预处理要求较高

模型优化

1. 核函数选择

   • 根据数据特征选择合适的核函数
   • 通过交叉验证确定最优核函数
   • 考虑计算复杂度和模型性能的平衡
   • 核函数参数的选择：
     • 多项式核的阶数$d$
     • 高斯核的带宽$\sigma$
     • Sigmoid核的参数$\beta$和$\theta$

2. 参数调优

   • 惩罚参数C的选择：
     • 使用网格搜索或随机搜索
     • 考虑数据的噪声水平
     • 平衡模型的复杂度和泛化能力
   • 核函数参数的选择：
     • 使用交叉验证
     • 考虑数据的分布特征
     • 避免过拟合和欠拟合

3. 数据预处理

   • 特征标准化：
     • 使用Z-score标准化
     • 使用Min-Max归一化
   • 特征选择：
     • 使用信息增益
     • 使用卡方检验
     • 使用L1正则化
   • 处理缺失值：
     • 使用均值填充
     • 使用中位数填充
     • 使用KNN填充
   • 处理类别不平衡：
     • 过采样
     • 欠采样
     • SMOTE算法

代码实现

from sklearn.svm import SVC
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd

# 创建SVM模型实例
model = SVC(
    kernel='rbf',           # 核函数：'linear', 'poly', 'rbf', 'sigmoid'
    C=1.0,                  # 惩罚参数
    gamma='scale',          # 核函数系数
    probability=True,       # 是否启用概率估计
    random_state=42
)

# 使用网格搜索找到最优参数
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': ['scale', 'auto', 0.1, 1, 10],
    'kernel': ['rbf', 'linear', 'poly']
}
grid_search = GridSearchCV(model, param_grid, cv=5)
grid_search.fit(X_train_scaled, y_train)

# 使用最优参数训练模型
best_model = grid_search.best_estimator_
best_model.fit(X_train_scaled, y_train)

# 在测试集上进行预测
y_pred = best_model.predict(X_test_scaled)
y_pred_proba = best_model.predict_proba(X_test_scaled)

# 计算评估指标
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='weighted')
recall = recall_score(y_test, y_pred, average='weighted')
f1 = f1_score(y_test, y_pred, average='weighted')

决策树

决策树是基于已知各种情况（特征取值）的基础上，通过构建树型决策结构来进行分析的一种方式，是常用的有监督的分类算法。它能够自动处理非线性关系和特征交互。

特点

• 优点：直观易懂、处理非线性关系和特征交互、对数据分布假设较少、支持多分类问题、对缺失值和异常值具有一定的鲁棒性。
• 缺点：过拟合倾向、不稳定性、全局最优性难以保证、对连续型特征的处理效率较低、特征重要性评估可能存在偏差。

原理

决策树（Decision tree）是基于已知各种情况（特征取值）的基础上，通过构建树型决策结构来进行分析的一种方式，是常用的有监督的分类算法。它能够自动处理非线性关系和特征交互。决策树的总体流程是自根至叶的递归过程，在每个中间结点寻找一个「划分」（split or test）属性。

主流的决策树算法有：

• ID3：基于信息增益来选择分裂属性（每步选择信息增益最大的属性作为分裂节点，树可能是多叉的）。
• C4.5：基于信息增益率来选择分裂属性（每步选择信息增益率最大的属性作为分裂节点，树可能是多叉的）。
• CART：基于基尼系数来构建决策树（每步要求基尼系数最小，树是二叉的）。
  其中CART树全称Classification And Regression Tree，既可以用于分类，也可以用于回归，这里指的回归树就是 CART 树，ID3和C4.5不能用于回归问题。

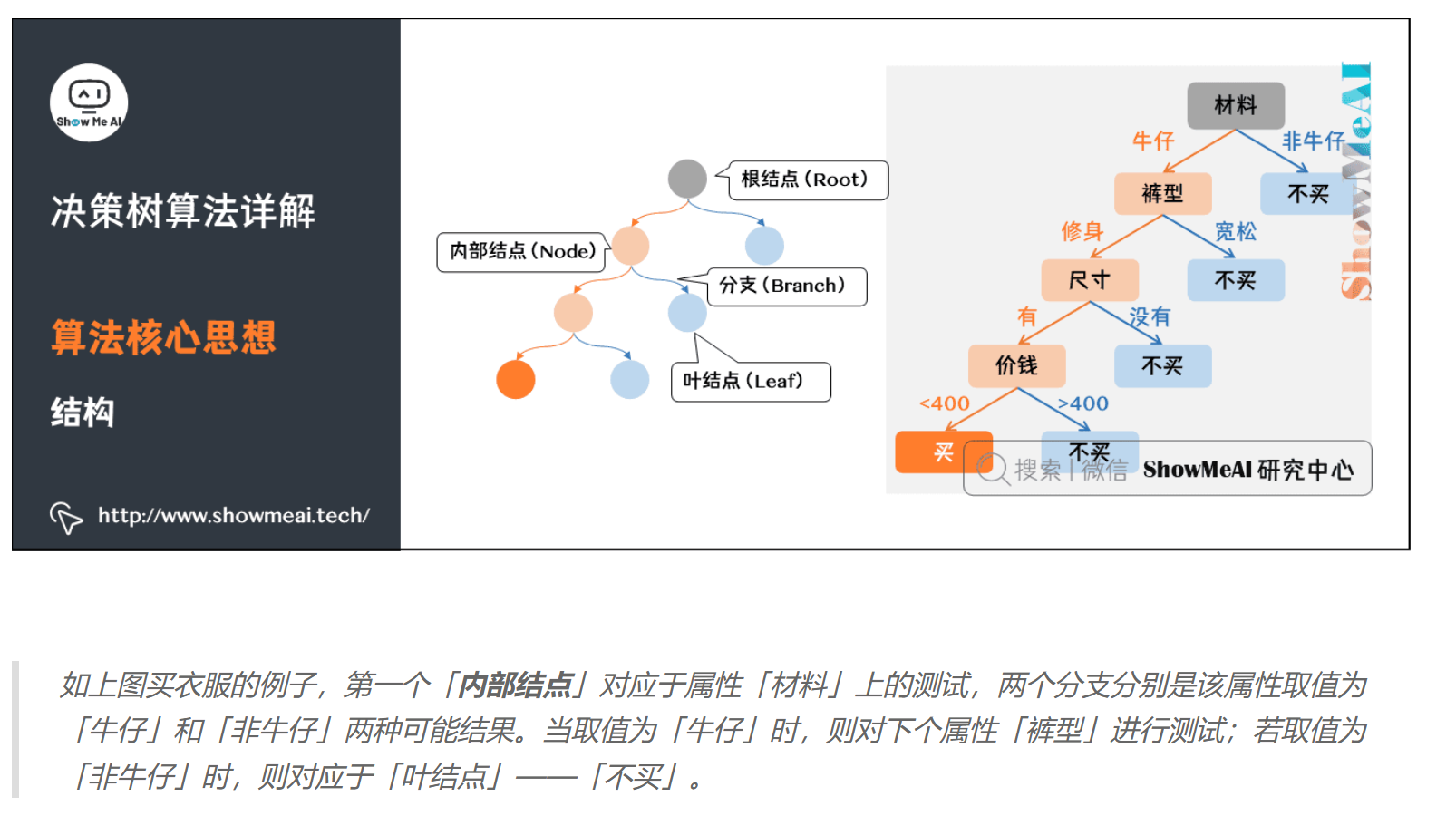
构造

• 每个内部结点表示一个属性的测试
• 每个分支表示一个测试输出
• 每个叶结点代表一种类别

损失函数

决策树的构建过程并不直接使用传统意义上的损失函数，而是通过分裂准则来选择最优的特征和分裂点。分裂准则是评估分裂质量的指标，目的是使分裂后的子节点尽可能纯净（即包含同一类别的样本）。

停止条件

• 当前结点包含的样全属于同一类别。无需划分。
• 样本的属性取值都相同或属性集为空。不能划分。
• 当前结点包含的样本集合为空。不能划分。

伪代码

核心概念

决策树如何实现最优划分属性选择：取得最大的信息增益。

1. 信息熵（Entropy）

   • 衡量数据的不确定性或混乱程度
   • 数学表达：$H(X) = -\sum_{i=1}^n p_i \log_2(p_i)$
   • 特点：
     • 熵值越大，数据越混乱
     • 熵值越小，数据越有序
     • 当所有类别概率相等时，熵最大

2. 信息增益（Information Gain）

   • 衡量特征对数据集的分类效果
   • 在决策树分类问题中，信息增益就是决策树在进行属性选择划分前和划分后的信息差值。
   • 计算方式：$IG = H(D) - H(D|A)$
   • 其中：
     • $H(D)$ 是数据集D的熵
     • $H(D|A)$ 是特征A条件下的条件熵
   • 特点：
     • 信息增益越大，特征越重要
     • 用于特征选择

3. 基尼系数（Gini Index）

   • 衡量数据的不纯度
   • 数学表达：$Gini(D) = 1 - \sum_{i=1}^n p_i^2$
   • 特点：
     • 值域在[0,1]之间
     • 值越小，数据越纯
     • 计算比熵更快

模型优化

过拟合问题

• 表现：
  • 训练集表现好，测试集表现差
  • 树结构过于复杂
  • 对噪声数据敏感
• 原因：
  • 训练数据不足
  • 特征过多
  • 树深度过大

如果让决策树一直生长，最后得到的决策树可能很庞大，、且易导致过拟合。缓解决策树过拟合可以通过剪枝操作完成。

• 预剪枝（Pre-pruning）：在树生长过程中进行剪枝，设置停止条件，如最大深度、最小样本数、最小信息增益等。
  • 优点：计算效率高
  • 缺点：可能欠拟合
• 后剪枝（Post-pruning）：先生长完整树，再剪枝，方法包括代价复杂度剪枝、错误率降低剪枝等。
  • 优点：效果更好
  • 缺点：计算成本高
• 特征选择与工程：选择对分类任务最有价值的特征，构造新特征，对连续型特征进行离散化处理等。
• 集成学习：通过组合多个决策树模型来提高分类性能和稳定性，如随机森林、梯度提升树、Adaboost等。

代码实现

from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd

# 创建决策树分类模型实例，并设置超参数
model = DecisionTreeClassifier(criterion='gini', max_depth=3, min_samples_split=2, min_samples_leaf=1, random_state=42)

# 在训练集上训练模型
model.fit(X_train_scaled, y_train)

# 在测试集上进行预测
y_pred = model.predict(X_test_scaled)
y_pred_proba = model.predict_proba(X_test_scaled)

# 计算评估指标
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
roc_auc = roc_auc_score(y_test, y_pred_proba)

随机森林

随机森林是一种由决策树构成的并行集成算法，属于Bagging类型，通过组合多个弱分类器，最终结果通过投票或取均值，使得整体模型的结果具有较高的精确度和泛化性能，同时也有很好的稳定性，广泛应用在各种业务场景中。

原理

集成学习

集成学习（ensemble learning）是一种将多个个体学习器组合成一个强学习器的方法。

个体学习器

• 同质集成：只包含同种类型的个体学习器，称作基学习器
  • 例如：随机森林中全是决策树集成
• 异质集成：包含不同类型的个体学习器，称作组件学习器
  • 例如：同时包含决策树和神经网络进行集成

核心问题

1. 个体学习器的选择

   • 不能太”弱”，需要有一定的准确性
   • 个体学习器之间要具有”多样性”，即存在差异性

2. 结合策略的选择

   • 并行组合方式：例如随机森林
   • 传统组合方式：例如boosting树模型

Bagging

Bagging是并行式集成学习方法最著名的代表。

Bootstrap Sampling

给定包含m个样本的数据集：

1. 随机取出一个样本放入采样集。
2. 将该样本放回初始数据集。
3. 重复m轮，得到m个样本的采样集。
4. 约63.2%的样本出现在采样集中。
5. 未出现的约36.8%的样本可用作验证集，来对后续的泛化性能进行「包外估计」。

流程

1. 重复采样T次，得到T个含m个训练样本的采样集
2. 基于每个采样集训练出一个基学习器
3. 对分类任务使用简单投票法
4. 对回归任务使用简单平均法

算法流程

1. 输入样本集D
2. 对于t=1,2,…,T：
   • 对训练集进行第t次随机采样，得到采样集Dt
   • 用采样集Dt训练第t个决策树模型Gt
   • 在节点划分时，随机选择部分特征
3. 分类场景：T个基模型投出最多票数的类别为最终类别

特点

核心特点

1. 随机性

   • 样本扰动：基于Bootstrap Sampling

     • 约63.2%的样本出现在采样集中
     • 带来数据集的差异化

   • 属性扰动：在节点划分时

     • 随机选择k个属性
     • 从k个属性中选择最优属性进行划分
     • 带来基模型的差异性

2. 集成性

   • 多个差异化采样集
   • 训练多个差异化决策树
   • 采用投票或平均法提高稳定性

优点

• 适用于高维稠密型数据
• 可判断特征重要程度
• 可构建组合特征
• 并行集成，控制过拟合
• 工程实现并行简单
• 对不平衡数据集友好
• 对特征缺失鲁棒性强

缺点

• 噪声过大时可能过拟合
• 模型解释较复杂

参数调优

核心参数

1. max_features：生成单颗决策树时的特征数

   • 增加：提高单树性能，降低树间差异
   • 减小：影响单树性能，影响整体效果
   • 需要平衡选择

2. n_estimators：决策树的棵树

   • 较多：提高稳定性和泛化能力
   • 较少：加快学习速度
   • 根据计算资源选择

3. max_depth：树深

   • 过大：可能导致过拟合
   • 过小：可能欠拟合
   • 根据样本量和特征数调整

参数选择

1. max_features：总数的百分比，常见选择区间[0.1, 0.9]
2. n_estimators：通常设置为[100, 1000]，根据计算资源调整
3. max_depth：常见选择在[3, 10]之间
4. min_samples_split：内部节点再划分所需最小样本数
   • 样本量不大：默认值
   • 样本量很大：可设置为[5, 10, 20]等
5. min_samples_leaf：叶子节点最少样本数，通常≥1

代码实现

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd

# 创建随机森林分类器实例
model = RandomForestClassifier(
    n_estimators=100,        # 决策树的数量
    max_features='sqrt',     # 特征选择方式
    max_depth=None,          # 树的最大深度
    min_samples_split=2,     # 分裂所需最小样本数
    min_samples_leaf=1,      # 叶节点最小样本数
    random_state=42
)

# 使用网格搜索找到最优参数
param_grid = {
    'n_estimators': [100, 200, 300],
    'max_features': ['sqrt', 'log2'],
    'max_depth': [None, 10, 20, 30],
    'min_samples_split': [2, 5, 10],
    'min_samples_leaf': [1, 2, 4]
}
grid_search = GridSearchCV(model, param_grid, cv=5)
grid_search.fit(X_train_scaled, y_train)

# 使用最优参数训练模型
best_model = grid_search.best_estimator_
best_model.fit(X_train_scaled, y_train)

# 在测试集上进行预测
y_pred = best_model.predict(X_test_scaled)
y_pred_proba = best_model.predict_proba(X_test_scaled)

# 计算评估指标
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='weighted')
recall = recall_score(y_test, y_pred, average='weighted')
f1 = f1_score(y_test, y_pred, average='weighted')

# 特征重要性分析
feature_importance = best_model.feature_importances_
sorted_idx = np.argsort(feature_importance)
print("特征重要性：", feature_importance[sorted_idx])

GBDT

GBDT（Gradient Boosting Decision Tree），全名叫梯度提升决策树，是一种迭代的决策树算法，又叫MART（Multiple Additive Regression Tree），它通过构造一组弱的学习器（树），并把多颗决策树的结果累加起来作为最终的预测输出。

原理

Boosting

Boosting方法训练基分类器时采用串行的方式，各个基分类器之间有依赖。它的基本思路是：

1. 将基分类器层层叠加
2. 每一层在训练时，对前一层基分类器分错的样本给予更高的权重
3. 测试时，根据各层分类器的结果的加权得到最终结果

与Bagging不同，Boosting在训练过程中，各基分类器之间有强依赖，必须串行训练。

GBDT详解

GBDT的核心原理：

1. 所有弱分类器的结果相加等于预测值
2. 每次都以当前预测为基准，下一个弱分类器去拟合误差函数对预测值的残差
3. GBDT的弱分类器使用的是树模型

GBDT与负梯度近似残差

回归任务下，GBDT在每一轮的迭代时对每个样本都会有一个预测值，此时的损失函数为均方差损失函数：

$L(y, F(x)) = \frac{1}{2}(y - F(x))^2$

损失函数的负梯度计算如下：

$-\frac{\partial L(y, F(x))}{\partial F(x)} = y - F(x)$

可以看出，当损失函数选用均方误差损失时，每一次拟合的值就是（真实值-预测值），即残差。

GBDT训练过程

1. 初始化模型，预测值为训练集标签的均值
2. 计算残差（实际值-预测值）
3. 训练新的决策树来拟合残差
4. 将新树的预测结果累加到原有预测结果上
5. 重复步骤2-4，直到达到指定的迭代次数或残差足够小

具体例子

假设我们要预测学生的考试成绩，特征包括：学习时间、作业完成率、课堂参与度等。

第一轮迭代：

1. 初始化：

   • 所有学生的预测值设为训练集平均分，假设为75分
   • 计算每个学生的残差（实际分数 - 75分）

2. 训练第一棵树：

   • 输入：学习时间、作业完成率、课堂参与度
   • 目标：预测残差
   • 例如：
     • 学生A：实际分数85分，残差为10分
     • 学生B：实际分数65分，残差为-10分
     • 学生C：实际分数80分，残差为5分

3. 更新预测值：

   • 学生A：75 + 10 = 85分
   • 学生B：75 + (-10) = 65分
   • 学生C：75 + 5 = 80分

第二轮迭代：

1. 计算新的残差：

   • 学生A：85 - 85 = 0分
   • 学生B：65 - 65 = 0分
   • 学生C：80 - 80 = 0分

2. 训练第二棵树：

   • 输入：相同的特征
   • 目标：预测新的残差
   • 由于残差已经很小，这棵树会很小或停止生长

最终预测：

• 将所有树的预测结果相加
• 例如：学生A的最终预测 = 75 + 10 + 0 = 85分

梯度提升 vs 梯度下降

两种迭代优化算法的对比：

1. 梯度下降

   • 模型以参数化形式表示
   • 模型的更新等价于参数的更新
   • 公式：$\theta_t = \theta_{t-1} - \eta \nabla L(\theta_{t-1})$

2. 梯度提升

   • 模型直接定义在函数空间中
   • 大大扩展了可使用的模型种类
   • 公式：$F_t(x) = F_{t-1}(x) - \eta \nabla L(F_{t-1}(x))$

具体例子对比

假设我们要优化一个简单的线性模型：$y = wx + b$

梯度下降：

1. 初始化参数：$w = 0, b = 0$
2. 计算梯度：$\frac{\partial L}{\partial w}, \frac{\partial L}{\partial b}$
3. 更新参数：
   • $w_{new} = w_{old} - \eta \frac{\partial L}{\partial w}$
   • $b_{new} = b_{old} - \eta \frac{\partial L}{\partial b}$

梯度提升：

1. 初始化模型：$F_0(x) = 0$
2. 计算负梯度：$-\frac{\partial L}{\partial F_0(x)}$
3. 训练新树$h_1(x)$拟合负梯度
4. 更新模型：$F_1(x) = F_0(x) + \eta h_1(x)$

特点

优点

• 预测阶段可并行化计算，计算速度快
• 适用稠密数据，泛化能力和表达能力都不错
• 可解释性不错，鲁棒性亦可
• 能够自动发现特征间的高阶关系

缺点

• 在高维稀疏数据集上效率较差
• 适合数值型特征，在NLP或文本特征上表现弱
• 训练过程无法并行
• 对异常值比较敏感

随机森林 vs GBDT

相同点

• 都是集成模型，由多棵树组成
• 最终结果都由多棵树一起决定
• 使用CART树时，可以是分类树或回归树

不同点

• 训练过程：随机森林可并行生成，GBDT只能串行生成
• 结果计算：随机森林是多数表决，GBDT是多棵树累加
• 异常值处理：随机森林对异常值不敏感，GBDT对异常值敏感
• 模型优化：随机森林降低方差，GBDT降低偏差

代码实现

import numpy as np
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import pydotplus
from sklearn.tree import export_graphviz
from IPython.display import Image

# 创建GBDT模型实例
model = GradientBoostingRegressor(
    n_estimators=100,        # 弱学习器的个数
    learning_rate=0.1,       # 学习率
    max_depth=3,             # 树的最大深度
    min_samples_split=2,     # 分裂所需最小样本数
    min_samples_leaf=1,      # 叶节点最小样本数
    subsample=1.0,           # 用于拟合个体学习器的样本比例
    random_state=42
)

# 训练模型
model.fit(X_train, y_train)

# 预测
y_pred = model.predict(X_test)

# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

# 可视化决策树
def visualize_tree(tree_index=0):
    sub_tree = model.estimators_[tree_index, 0]
    dot_data = export_graphviz(
        sub_tree,
        out_file=None,
        filled=True,
        rounded=True,
        special_characters=True,
        precision=2
    )
    graph = pydotplus.graph_from_dot_data(dot_data)
    return Image(graph.create_png())

# 特征重要性分析
feature_importance = model.feature_importances_
sorted_idx = np.argsort(feature_importance)
print("特征重要性：", feature_importance[sorted_idx])

XGBoost

XGBoost（eXtreme Gradient Boosting）是一个强大的Boosting算法工具包，在数据科学竞赛中表现优异，现在很多大厂的机器学习方案都会首选这个模型。XGBoost在并行计算效率、缺失值处理、控制过拟合、预测泛化能力上都表现非常优秀。

原理

基本概念

1. Boosting集成学习

   • 串行训练多个弱学习器
   • 每个弱学习器关注之前模型预测错误的样本
   • 最终结果由所有弱学习器加权组合

2. XGBoost的核心思想

   • 使用CART回归树作为基学习器
   • 通过梯度提升的方式训练模型
   • 使用二阶导数信息优化目标函数
   • 加入正则化项控制模型复杂度

3. 目标函数设计

   • 总体目标函数：$Obj(\Theta) = L(\Theta) + \Omega(\Theta)$
     • $L(\Theta)$：训练损失函数，衡量模型预测值与真实值的差距
     • $\Omega(\Theta)$：正则化项，控制模型复杂度
   • 第t次迭代的目标函数：
     $Obj^{(t)} = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t)$
     • $\hat{y}_i^{(t-1)}$：前t-1棵树的预测结果
     • $f_t(x_i)$：第t棵树的预测结果
     • 意义：每次迭代都优化当前树的预测结果，同时考虑模型复杂度

4. 泰勒展开近似

   • 展开过程：
     $l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) \approx l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2}h_i f_t^2(x_i)$
     • $g_i = \frac{\partial l(y_i, \hat{y}_i^{(t-1)})}{\partial \hat{y}_i^{(t-1)}}$：一阶导数
     • $h_i = \frac{\partial^2 l(y_i, \hat{y}_i^{(t-1)})}{\partial (\hat{y}_i^{(t-1)})^2}$：二阶导数
   • 意义：
     • 将复杂的损失函数近似为二次函数
     • 便于计算最优解
     • 提高计算效率

5. 正则化项设计

   • 树的复杂度定义：
     $\Omega(f_t) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2$
     • $T$：叶子节点个数，控制树的深度
     • $w_j$：第j个叶子节点的权重，控制节点预测值
     • $\gamma, \lambda$：控制正则化强度的超参数
   • 意义：
     • 控制树的生长，防止过拟合
     • 平衡模型的复杂度和预测能力
     • 提高模型的泛化能力

树的生成过程

1. 节点分裂

   • 贪心算法：遍历所有特征和所有可能的分裂点

   • 分裂收益计算：
     $Gain = \frac{1}{2}[\frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda}] - \gamma$

     • $G_L, G_R$：左右子节点的一阶导数之和
     • $H_L, H_R$：左右子节点的二阶导数之和

   • 意义：

     • 衡量分裂前后的损失减少程度
     • 考虑正则化项的影响
     • 指导最优分裂点的选择

   • 具体例子：
     假设我们要预测房价，特征包括：面积、位置、房龄等

     • 第一步：选择”面积”作为第一个分裂特征，将样本分为”大户型”和”小户型”
     • 第二步：在”大户型”中，可能用”位置”继续分裂
     • 第三步：在”小户型”中，可能用”房龄”继续分裂
     • 最终：每个叶子节点都会给出一个预测值（房价）

     分裂点选择过程：

     • 遍历所有可能的面积值（如：50㎡, 60㎡, 70㎡…）
     • 对每个值，计算分裂后的左右子节点的梯度统计量
     • 选择使Gain最大的面积值作为分裂点

2. 叶子节点权重计算

   • 最优权重：
     $w_j^* = -\frac{G_j}{H_j + \lambda}$

     • $G_j$：该叶子节点所有样本的一阶导数之和
     • $H_j$：该叶子节点所有样本的二阶导数之和

   • 意义：

     • 使目标函数最小化
     • 考虑样本的梯度信息
     • 平衡预测准确性和模型复杂度

   • 具体例子：
     假设一个叶子节点包含3个样本：

     • 样本1：$g_1=0.5, h_1=1.0$
     • 样本2：$g_2=0.3, h_2=0.8$
     • 样本3：$g_3=0.4, h_3=0.9$
     • $G_j = 0.5 + 0.3 + 0.4 = 1.2$
     • $H_j = 1.0 + 0.8 + 0.9 = 2.7$
     • 假设$\lambda = 1$，则$w_j^* = -\frac{1.2}{2.7 + 1} = -0.32$

3. 停止条件

   • 达到最大深度

   • 分裂收益小于阈值

   • 叶子节点样本数小于阈值

   • 意义：

     • 控制树的生长
     • 防止过拟合
     • 提高计算效率

   • 具体例子：

     • 最大深度：设置max_depth=3，则树最多有3层
     • 最小分裂收益：设置min_gain=0.1，则Gain<0.1时停止分裂
     • 最小样本数：设置min_samples=10，则样本数<10时停止分裂

4. 实际训练过程

   • 第一步：初始化

     • 所有样本的预测值设为0
     • 计算初始梯度$g_i$和$h_i$

   • 第二步：迭代训练

     • 对每棵树：
       1. 计算所有样本的梯度
       2. 选择最佳分裂特征和分裂点
       3. 生成新的子节点
       4. 计算叶子节点权重
       5. 更新所有样本的预测值

   • 第三步：预测

     • 将样本从根节点开始，按照分裂规则向下遍历
     • 到达叶子节点后，使用该节点的权重作为预测值
     • 将所有树的预测值相加得到最终预测

优化策略

1. 近似算法

   • 分位数划分：
     • 将特征值按分位数划分
     • 减少候选分裂点数量
     • 提高计算效率
   • 全局/局部策略：
     • 全局：在根节点分裂前计算一次
     • 局部：每个节点分裂前都计算
     • 平衡计算效率和精度

2. 特征缺失处理

   • 稀疏感知：
     • 将缺失值和稀疏值等同处理
     • 跳过缺失值的整体
     • 提高计算效率
   • 分裂方向：
     • 考虑缺失值的两个方向
     • 选择最优的分裂方向
     • 提高模型鲁棒性

3. 并行计算

   • 特征预排序&块式存储
   • XGBoost 将每一列特征提前进行排序，以块（Block）的形式储存在缓存中，并以索引将特征值和梯度统计量对应起来，每次节点分裂时会重复调用排好序的块。而且不同特征会分布在独立的块中，因此可以进行分布式或多线程的计算。
   • 缓存访问优化
   • 特征值排序后通过索引来取梯度$g_i$、$h_i$会导致访问的内存空间不一致，进而降低缓存的命中率，影响算法效率。为解决这个问题，XGBoost为每个线程分配一个单独的连续缓存区，用来存放梯度信息。
   • 核外块计算
   • 数据量非常大的情形下，无法同时全部载入内存。XGBoost 将数据分为多个 blocks 储存在硬盘中，使用一个独立的线程专门从磁盘中读取数据到内存中，实现计算和读取数据的同时进行。
   • 为了进一步提高磁盘读取数据性能，XGBoost 还使用了两种方法：
     • ① 压缩 block，用解压缩的开销换取磁盘读取的开销。
     • ② 将 block 分散储存在多个磁盘中，提高磁盘吞吐量。

特点

1. 优势

1. 精度高

   • 使用二阶导数信息
   • 支持自定义损失函数
   • 正则化控制过拟合

2. 效率高

   • 特征预排序
   • 并行计算
   • 缓存优化

3. 实用性强

   • 支持缺失值处理
   • 支持早停
   • 支持特征重要性评估

2. 局限性

1. 计算资源需求

   • 需要较大的内存
   • 训练时间可能较长
   • 参数调优复杂

2. 数据要求

   • 对异常值敏感
   • 需要足够的训练数据
   • 特征工程要求高

代码实现

import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import numpy as np

# 创建XGBoost模型实例
model = xgb.XGBRegressor(
    n_estimators=100,        # 弱学习器的个数
    learning_rate=0.1,       # 学习率
    max_depth=3,             # 树的最大深度
    min_child_weight=1,      # 叶子节点最小样本权重和
    subsample=0.8,           # 训练每棵树时使用的样本比例
    colsample_bytree=0.8,    # 训练每棵树时使用的特征比例
    gamma=0,                 # 分裂所需的最小损失函数下降值
    reg_alpha=0,             # L1正则化项
    reg_lambda=1,            # L2正则化项
    random_state=42
)

# 训练模型
model.fit(
    X_train, 
    y_train,
    eval_set=[(X_test, y_test)],
    eval_metric='rmse',
    early_stopping_rounds=10,
    verbose=True
)

# 预测
y_pred = model.predict(X_test)

# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

# 特征重要性分析
feature_importance = model.feature_importances_
sorted_idx = np.argsort(feature_importance)
print("特征重要性：", feature_importance[sorted_idx])

# 可视化决策树
xgb.plot_tree(model, num_trees=0)
xgb.plot_importance(model)

LightGBM

LightGBM是微软开发的boosting集成模型，是对GBDT的优化和高效实现。相比XGBoost，它在训练效率、内存使用、准确率等方面都有显著提升。

原理

开发动机

1. 大数据量下的GBDT问题

   • 传统GBDT每次迭代需要遍历整个训练数据多次
   • 数据量大时面临内存限制
   • 反复读写训练数据消耗大量时间
   • 工业级海量数据下效率不足

2. XGBoost的局限性

   • 精确贪心算法：

     • 优点：可以找到精确的划分条件
     • 缺点：计算量巨大、内存占用巨大、易产生过拟合

   • Level-wise生长方式：

     • 优点：可以使用多线程、加速精确贪心算法
     • 缺点：效率低下，可能产生不必要的叶结点
     • 原理：按层生长，每次同时分裂同一层的所有叶子节点
     • 具体过程：
       • 从根节点开始，第一层只有一个节点
       • 第二层同时分裂所有节点，产生多个子节点
       • 第三层再次同时分裂所有节点
       • 以此类推，直到达到最大深度
         • 假设最大深度为3——第一层：根节点；第二层：同时分裂根节点，得到2个子节点；第三层：同时分裂第二层的2个节点，得到4个叶子节点
     • 问题：
       • 同一层的节点可能增益差异很大
       • 低增益的节点也被强制分裂
       • 增加了不必要的计算开销

   • Cache优化不友好：

     • 特征对梯度的访问是随机访问
     • 不同特征访问顺序不一致
     • 造成较大的cache miss

核心优化点

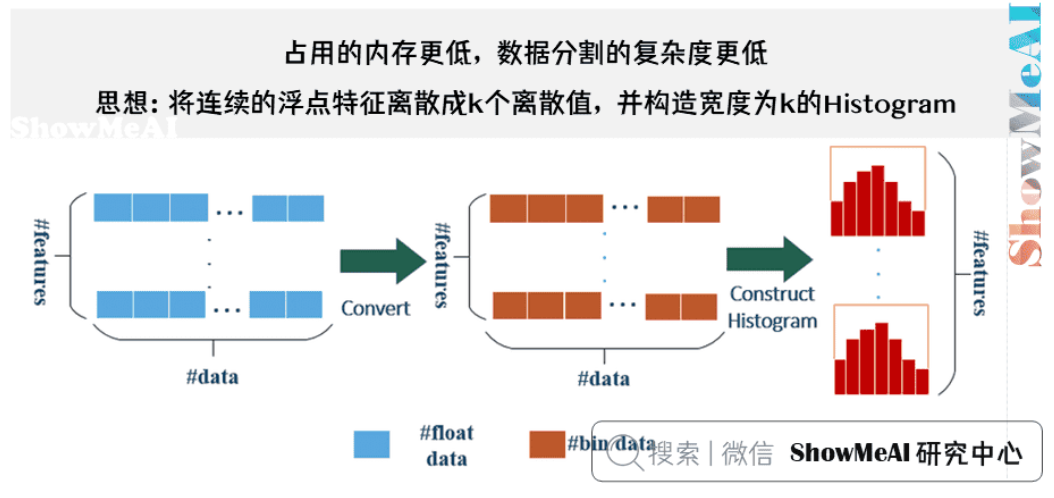
1. 基于Histogram的决策树算法

   • 原理：

     • 将连续的浮点特征离散成k个离散值，并构造宽度为k的Histogram。
     • 遍历训练数据，统计每个离散值在直方图中的累计统计量（统计每个区间的样本数量、梯度等信息；每个区间用一个值表示（如：区间中点））。
     • 在进行特征选择时，只需要根据直方图的离散值，遍历寻找最优的分割点。

   • Histogram（直方图）详解：

     • 定义：一种数据分布的图形表示，将数据范围分成若干个区间，统计每个区间的数据频数
     • 在LightGBM中的应用：
       • 将连续特征值域范围分成k个等宽区间
       • 每个区间称为一个bin（桶）
       • 对每个bin统计：
         • 样本数量
         • 一阶梯度之和
         • 二阶梯度之和

   • 优势：

     • 内存优化：从O(#data)降低到O(#bins)
     • 计算量优化：时间复杂度从O(#data)降低到O(#bins)
     • 正则化效果：分桶操作本身具有正则化作用，可以防止过拟合

   • 具体例子：
     假设有一个”用户年龄”特征，取值范围是18-60岁：

     • 传统方法：需要存储每个用户的精确年龄，排序后遍历所有可能的分裂点
     • LightGBM方法：将年龄分成8个区间，每个区间用中点表示，只需要存储8个值

2. 带深度限制的Leaf-wise叶子生长策略

   • 原理：

     • 每次选择增益最大的叶子节点进行分裂
     • 与Level-wise（按层生长）不同
     • 可以更快地降低损失函数

   • 优势：

     • 更快的收敛速度
     • 更好的模型精度
     • 更少的树节点

   • 具体例子：
     假设我们在预测房价，特征包括：面积、位置、房龄等

     • Level-wise生长：同时分裂同一层的所有叶子节点
     • Leaf-wise生长：每次只选择增益最大的叶子节点进行分裂

3. 直方图做差加速

   • 原理：

     • 利用直方图的特性，通过做差的方式计算分裂增益
     • 减少重复计算
     • 提高计算效率

   • 直方图特性：

     • 可加性：
       • 两个相邻区间的统计信息可以合并
       • 例如：bin1和bin2的样本数之和等于bin1+2的样本数
       • 梯度信息也具有可加性
     • 可减性：
       • 从父节点的统计信息中减去子节点的统计信息
       • 例如：父节点样本数 - 左子节点样本数 = 右子节点样本数
       • 避免重复计算子节点的统计信息
     • 局部性：
       • 相邻区间的统计信息变化较小
       • 可以利用缓存提高访问效率
       • 减少内存访问开销
     • 稀疏性：
       • 很多区间的统计信息可能为0
       • 可以跳过这些区间的计算
       • 进一步提高计算效率

   • 优势：

     • 减少计算量
     • 提高训练速度
     • 降低内存使用

4. 直接支持类别特征

   • 原理：

     • 无需one-hot编码
     • 直接使用类别特征
     • 在分裂时，尝试不同的类别组合

   • 优势：

     • 更高效的特征处理，可以找到最优的类别组合
     • 不需要one-hot编码，降低内存使用
     • 提高计算效率：时间复杂度为O(k)，k为类别数量

   • 具体例子：
     假设有一个”用户等级”特征，取值为：普通、银卡、金卡、钻石

     • 传统方法：需要one-hot编码，特征维度从1维变成4维
     • LightGBM方法：直接使用类别特征，在分裂时尝试不同的类别组合
       • 分裂过程示例：
         • 第一次尝试：{普通, 银卡} vs {金卡, 钻石}
         • 第二次尝试：{普通, 金卡} vs {银卡, 钻石}
         • 第三次尝试：{普通, 钻石} vs {银卡, 金卡}
         • 第四次尝试：{普通} vs {银卡, 金卡, 钻石}
         • 以此类推，尝试所有可能的组合
       • 计算每种组合的增益：
         • 统计每个组合中的样本数量
         • 计算每个组合的梯度信息
         • 选择增益最大的组合作为分裂点

5. Cache命中率优化

   • 原理：

     • 优化内存访问模式
     • 提高cache命中率
     • 减少cache miss

   • 优势：

     • 提高内存访问效率
     • 减少计算时间
     • 提高训练速度

6. 基于直方图的稀疏特征优化

   • 原理：

     • 高效处理稀疏数据
     • 降低内存使用
     • 提高计算效率

   • 优势：

     • 更好的处理稀疏特征
     • 降低内存使用
     • 提高训练速度

7. 多线程优化

   • 原理：

     • 支持并行计算
     • 提高训练效率
     • 充分利用多核CPU

   • 优势：

     • 更快的训练速度
     • 更好的资源利用
     • 支持大规模数据

算法对比

1. XGBoost：Pre-sorted算法

   • 流程：

     • 对所有特征按数值进行预排序
     • 每次分割时用O(#data)的代价找到最优分割点
     • 找到最终特征和分割点，分裂数据

   • 缺点：

     • 内存需要训练数据的两倍
     • 遍历分割点时需要计算分裂增益
     • 计算代价大

• 精确贪心算法
  • 原理：精确贪心算法是指每一轮分裂时，遍历所有特征的所有可能分割点，计算每个分割点的分裂增益，选择增益最大的分割点进行分裂。每次分割都能找到最优的分割点，因此理论上分裂点最优。但每轮都需要遍历整个训练数据多次，计算量和内存消耗都非常大。如果把全部训练数据装进内存，会限制数据规模；如果不装进内存，反复读写训练数据又会消耗大量时间。
    • 分裂增益公式：
      $$ Gain = \frac{1}{2} \left[ \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} \right] - \gamma $$
      其中：
      • $G_L, H_L$：分割后左子树的一阶、二阶梯度和
      • $G_R, H_R$：分割后右子树的一阶、二阶梯度和
      • $\lambda$：正则化参数
      • $\gamma$：叶子节点复杂度惩罚项
      • $(G_L + G_R), (H_L + H_R)$：分割前节点的梯度和
    • 公式解释：
      • 第一项：分割后左子树的得分
      • 第二项：分割后右子树的得分
      • 第三项：分割前节点的得分
      • 第四项：增加一个节点的复杂度惩罚
    • 优点：
      • 可以找到最精确的划分条件，理论上分裂点最优。
    • 缺点：
      • 计算量巨大，内存占用大，尤其在大数据场景下效率低下。
      • 容易产生过拟合，因为每次都能找到最优分割，模型复杂度高。
      • 每一轮分裂时，遍历所有特征的所有可能分割点，计算上述公式，选择增益最大的分割点进行分裂。
      • 这种方式虽然精确，但在大数据下会极大拖慢训练速度，且对内存要求高。

2. LightGBM：直方图算法

   • 思想：

     • 将连续特征离散成k个离散值
     • 构造宽度为k的直方图
     • 根据直方图寻找最优分割点

   • 优势：

     • 内存优化：不需要存储预排序结果
     • 计算量优化：时间复杂度从O(#data)降到O(k)
     • 正则化效果：分桶bin替代原始数据

   • 注意点：

     • 分桶bin数量决定正则化程度
     • bin越少惩罚越严重，欠拟合风险越高
     • 预先设定bin范围，无需排序
     • 直方图保存划分阈值、样本数、梯度信息

策树生长策略

1. XGBoost：Level-wise

   • 同时分裂同一层的叶子
   • 支持多线程优化
   • 不容易过拟合
   • 可能产生不必要的分裂

2. LightGBM：Leaf-wise

   • 每次找到分裂增益最大的叶子
   • 降低更多误差
   • 得到更好精度
   • 可能产生过深的树
   • 通过最大深度限制防止过拟合

5. 类别特征支持

1. 传统方法的问题

   • one-hot编码效率低
   • 可能无法在类别特征上切分
   • 数据切分过于零碎
   • 统计信息不准确

2. LightGBM的解决方案

   • 采用Many vs Many的切分方式
   • 直接输入类别特征
   • 实现类别特征的最优切分
   • 时间复杂度从O(2^k)优化到O(k)

3. 具体流程

   • 建立直方图：

     • 统计离散值出现次数
     • 过滤低频特征值
     • 建立bin容器

   • 计算分裂阈值：

     • 根据bin容器数量选择策略
     • 使用one vs other或many vs many
     • 计算最优分裂点

   • 特征分裂：

     • 根据阈值集合划分数据
     • 决定样本归属

6. 并行优化

1. 特征并行

   • 不同机器处理不同特征
   • 本地保存全部数据
   • 避免数据切分通信

2. 数据并行

   • 本地构造直方图
   • 全局合并
   • 寻找最优分割点
   • 使用分散规约降低通信量

3. 网络通信优化

   • 使用histogram算法降低通信代价
   • 实现并行计算的线性加速
   • 支持大规模分布式训练

代码实现

import lightgbm as lgb
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import numpy as np

# 创建LightGBM模型实例
model = lgb.LGBMRegressor(
    n_estimators=100,        # 弱学习器的个数
    learning_rate=0.1,       # 学习率
    max_depth=3,             # 树的最大深度
    num_leaves=31,           # 叶子节点数
    min_child_samples=20,    # 叶子节点最小样本数
    subsample=0.8,           # 训练每棵树时使用的样本比例
    colsample_bytree=0.8,    # 训练每棵树时使用的特征比例
    reg_alpha=0,             # L1正则化项
    reg_lambda=1,            # L2正则化项
    random_state=42
)

# 训练模型
model.fit(
    X_train, 
    y_train,
    eval_set=[(X_test, y_test)],
    eval_metric='rmse',
    early_stopping_rounds=10,
    verbose=True
)

# 预测
y_pred = model.predict(X_test)

# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

# 特征重要性分析
feature_importance = model.feature_importances_
sorted_idx = np.argsort(feature_importance)
print("特征重要性：", feature_importance[sorted_idx])

# 可视化决策树
lgb.plot_tree(model, tree_index=0)
lgb.plot_importance(model)