机器学习模型评估方法与准则

参考：https://www.showmeai.tech/

基本概念

核心目标：选出泛化能力强的模型完成机器学习任务
实际挑战：需进行大量实验，涉及反复调参、多种模型算法（甚至多模型融合）的尝试，以确定最优模型与参数组合
泛化能力定义：模型能很好地适用于未知样本，表现为低错误率、高精度。理想模型应能准确预测未知样本的标签
实现路径：基于已有数据切分完成训练和评估，通过评估方法判断模型状态（过拟合/欠拟合）并迭代优化

离线与在线实验方法

离线实验方法

适用阶段：原型设计（Prototyping）阶段
核心流程：
1. 使用历史数据训练一个或多个模型
2. 对模型进行验证与离线评估
3. 通过评估指标选择较优模型
关键作用：通过数据切分（训练集/测试集）模拟未知样本，评估模型状态

在线实验方法

必要性：离线数据与线上实时数据分布可能存在差异
核心方法：A/B测试 笔记:ABtest
- 定义：为同一目标制定两个方案（A和B），将用户分为两组分别使用不同方案，记录行为数据比较效果
- 重要性：避免未经验证的新方案对产品造成负面影响
- 执行要点：确保分组随机性，控制单一变量，设置足够样本量
典型场景：新模型/策略上线前的效果验证

对应评估指标

离线评估指标：
- 准确率（Accuracy）
- 查准率（Precision）
- 召回率（Recall）
- ROC曲线
- AUC值
- PR曲线
在线评估指标：
- 用户生命周期值（Customer Lifetime Value）
- 广告点击率（Click Through Rate）
- 用户流失率（Customer Churn Rate）
- 转化率（Conversion Rate）
- 留存率（Retention Rate）

方法论

留出法

Hold-out

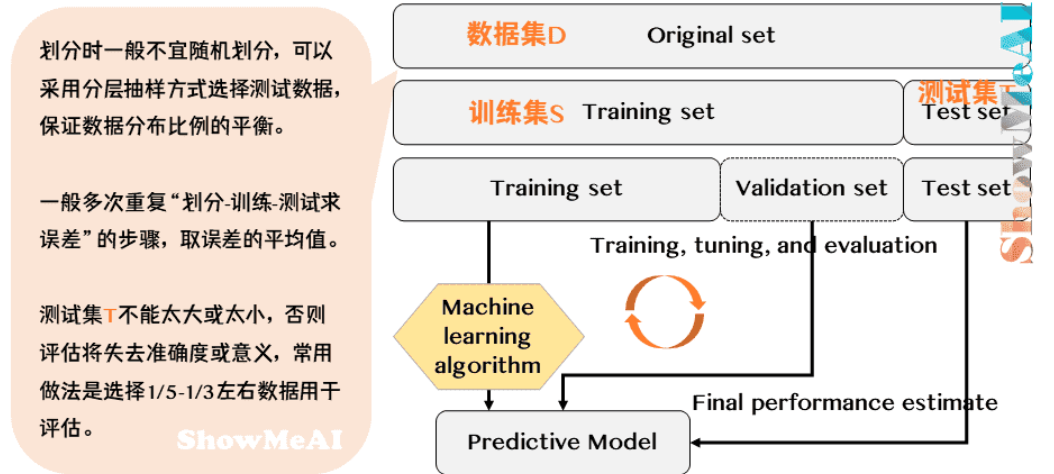
基本原理：将数据集D划分为互斥的训练集S和测试集T（通常|T|/|D|≈0.2~0.3）
关键注意事项：
- 分层抽样：当随机划分不一定能保证有效性，因为如果T中正好只取到某一种特殊类型数据，从而带来了额外的误差。此时处理方法要视具体情况而定，如当数据明显的分为有限类时，可以采用分层抽样方式选择测试数据，需保持划分后数据分布比例一致。
- 多次重复：单次划分不一定能得到合适的测试集，需多次重复”划分-训练-测试”过程，保证数据分布比例的平衡。
- 验证集大小：过小导致评估不稳定，过大削弱训练数据量。常用做法是选择1/3-1/5左右数据当作验证集用于评估。
优化变体：分层留出法（Stratified Hold-out） 保持类别分布均衡

交叉验证法

Cross Validation

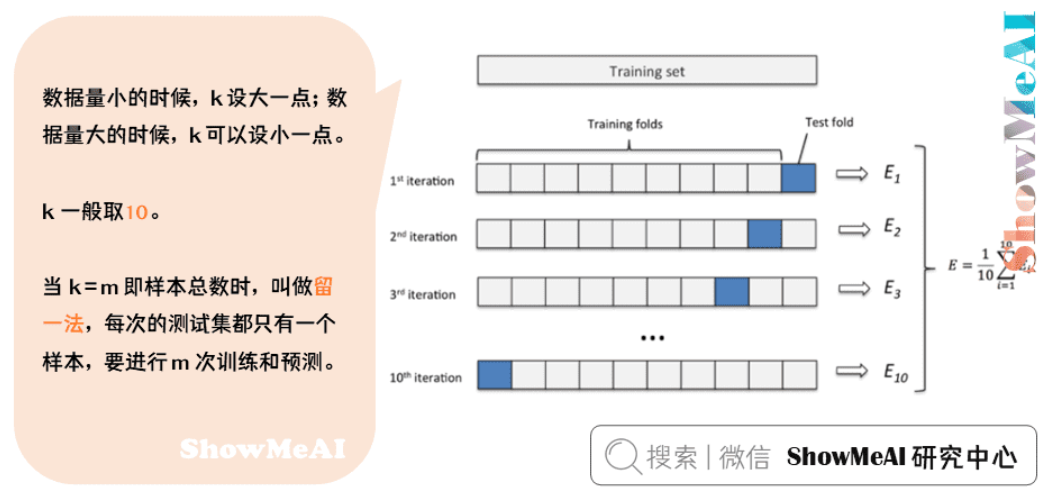
k折交叉验证流程：
1. 将数据集随机划分为k个大小相等的互斥子集
2. 每次用k-1个子集训练模型，剩余1个子集测试
3. 重复k次，每次使用不同子集测试
4. 汇总k次评估结果取平均值
核心优势：
- 显著降低数据划分引入的方差
- 充分利用有限数据，评估结果更稳定可靠
- 特别适合小数据集评估
特殊形式：
- 留一交叉验证（LOOCV）：k等于样本数，每次仅留一个样本测试
- 分层交叉验证：保持每折中类别分布与原数据集一致

自助法

Bootstrap

适用场景：数据量较少时估计整体分布
核心原理：通过有放回抽样生成大量伪样本，模拟数据分布
数学基础：
- 样本在m次自助采样中未被选中的概率：lim(m→∞)(1-1/m)^m → 1/e ≈ 0.368
- 约36.8%的原始数据不会出现在自助样本中（袋外样本）
实施步骤：
1. 从原始数据集D中有放回抽取n个样本形成新训练集
2. 用未抽中的样本作为测试集
3. 重复多次取评估结果平均
核心优势：可估计统计量的置信区间（如误差的置信区间）

回归问题评估指标体系

平均绝对误差（MAE）

计算公式：$$MAE = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i|$$
核心优势：直观反映预测值与实际值的平均偏差程度，量纲与原始数据一致
主要局限：无法反映预测值的无偏性，对异常值不敏感
适用场景：需要直观理解平均误差大小的业务场景

平均绝对百分误差（MAPE）

计算公式：$$MAPE = \frac{100%}{n} \sum_{i=1}^n \left| \frac{y_i - \hat{y}_i}{y_i} \right|$$
核心优势：考虑误差相对真实值的比例，便于跨量级比较
主要局限：当真实值接近零时计算不稳定
典型应用：房价预测等量级差异大的场景

均方误差（MSE）

计算公式：$$MSE = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2$$
核心特性：
- 放大较大误差的影响
- 对异常值敏感
- 函数光滑可导，便于优化
主要局限：数值量纲与原始数据不一致

均方根误差（RMSE）

计算公式：$$RMSE = \sqrt{MSE}$$
核心优势：恢复量纲一致性，更接近真实误差水平
应用场景：需要误差值与原始数据同量级的业务报告

决定系数（R²）

计算公式：$$R^2 = 1 - \frac{\sum_{i=1}^n (y_i - \hat{y}i)^2}{\sum{i=1}^n (y_i - \bar{y})^2}$$
统计含义：模型解释的目标变量方差占比
取值范围：[0,1] 越接近1表示模型解释能力越强
核心优势：无量纲指标，便于比较不同数据集上的模型
主要局限：随特征数量增加而提高，可能误导模型选择

校正决定系数（Adjusted R²）

计算公式：$$Adjusted\ R^2 = 1 - \frac{(1-R^2)(n-1)}{n-p-1}$$
- 其中p为特征数量，n为样本量
核心改进：惩罚特征数量增加，避免过拟合
典型应用：比较不同特征数量的回归模型

适用场景

模型开发阶段：优先使用MSE/RMSE（可导性利于优化）
业务报告场景：优先使用MAE/MAPE（直观易解释）
模型选择阶段：优先使用Adjusted R²（避免特征数量干扰）
跨模型比较：R²提供无量纲的统一评估基准

分类问题评估指标体系

指标中文	英文/缩写	公式
精确率	Accuracy	$$Accuracy = \frac{TP + TN}{FP + FN + FP + TN}$$
查准率	Precision	$$Precision = \frac{TP}{TP + FP}$$
查全率	Recall	$$Recall = \frac{TP}{TP + FN}$$
Fβ-Score	Fβ-Score	$$F_\beta = \frac{(1+\beta^2) \cdot Precision \cdot Recall}{\beta^2 \cdot Precision + Recall}$$
F1-Score	F1-Score	$$F_1 = \frac{2 \cdot Precision \cdot Recall}{Precision + Recall}$$
真正例率	TPR	$$TPR = \frac{TP}{TP + FN}$$
假正例率	FPR	$$FPR = \frac{FP}{FP + TN}$$
ROC曲线	ROC	-
AUC值	AUC	-
PR曲线	PRC	-

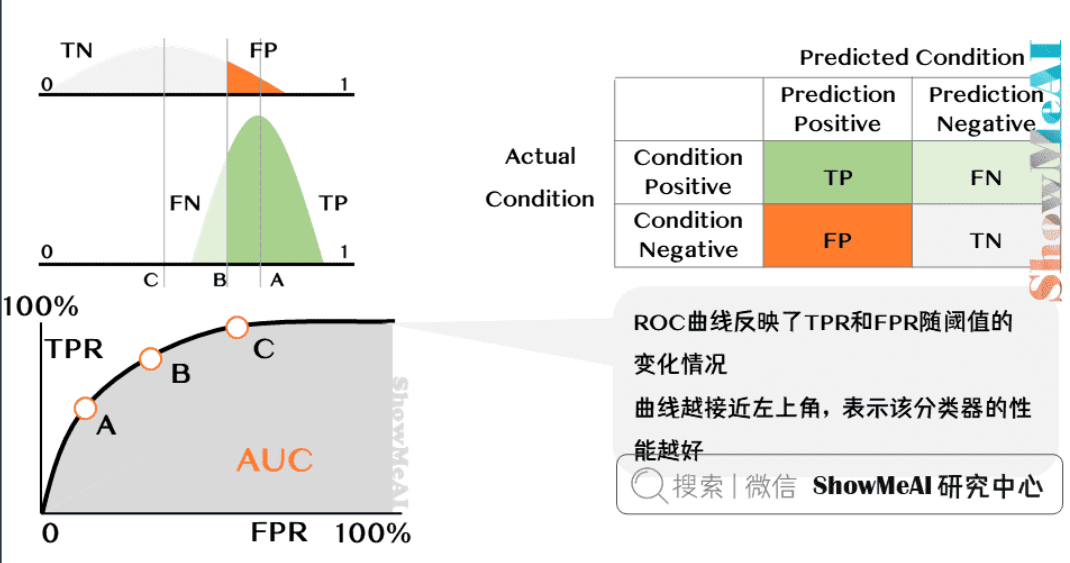
混淆矩阵（Confusion Matrix）

核心结构：
- True Positive（TP）：正类预测正确
- False Positive（FP）：负类误判为正类（I类错误）
- False Negative（FN）：正类误判为负类（II类错误）
- True Negative（TN）：负类预测正确

矩阵可视化：

1
2
3

            预测正类    预测负类
实际正类      TP          FN
实际负类      FP          TN

准确率（Accuracy）

计算公式：$$Accuracy = \frac{TP+TN}{TP+FP+FN+TN}$$
核心优势：全局性能的直观度量
主要局限：在类别不平衡时可能产生误导
适用条件：各类别样本量均衡的场景

精确率/查准率（Precision）

计算公式：$$Precision = \frac{TP}{TP+FP}$$
业务含义：预测为正类的样本中实际为正类的比例
核心价值：衡量”宁缺毋滥”程度
典型场景：垃圾邮件识别（减少误判正常邮件）

召回率/查全率（Recall）

计算公式：$$Recall = \frac{TP}{TP+FN}$$
业务含义：实际为正类的样本中被正确识别的比例
核心价值：衡量”宁可错杀”程度
典型场景：癌症筛查（避免漏诊）

Fβ分数（Fβ-Score）

计算公式：$$F_\beta = \frac{(1+\beta^2) \cdot Precision \cdot Recall}{\beta^2 \cdot Precision + Recall}$$
参数意义：
- β=1：平衡精确率和召回率（F1分数）
- β>1：更重视召回率
- β<1：更重视精确率
F1特殊形式：F1 = 2 * (Precision*Recall) / (Precision+Recall)

ROC曲线

Receiver Operating Characteristic

核心指标：
- 真正例率 TPR = Recall = TP/(TP+FN)
- 假正例率 FPR = FP/(FP+TN)
绘制方法：
1. 将样本按预测概率降序排列
2. 从高到低移动阈值，计算每个阈值下的TPR/FPR
3. 连接所有点形成曲线
曲线特性：
- 对角线表示随机猜测
- 左上角为理想状态
- 曲线下凸表示分类器有效

AUC

Area Under ROC Curve

定义：ROC曲线下方面积
统计意义：随机选取的正样本得分高于负样本的概率
取值范围：[0.5, 1] 越接近1性能越好
核心优势：
- 不受分类阈值影响
- 对样本比例不敏感
- 反映模型整体排序能力

PR曲线

Precision-Recall Curve

绘制方法：
1. 将样本按预测概率降序排列
2. 从高到低移动阈值，计算每个阈值下的Precision/Recall
3. 连接所有点形成曲线
适用场景：
- 正负样本极不平衡时（如欺诈检测）
- 更关注正类样本识别的任务
与ROC对比：
- PR曲线对类别比例变化更敏感
- 正样本极少时PR曲线提供更丰富信息

样本不均衡解决方案

数据采样技术

欠采样

Undersampling
欠采样技术是将数据从原始数据集中移除。

从多数类集合中筛选样本集E。
将这些样本从多数类集合中移除。
实施方法：从多数类中筛选代表性样本子集
典型算法：
- 随机欠采样（Random Undersampling）
  - 原理：随机从多数类中删除样本，直到达到期望的类别比例
  - 优点：实现简单，计算效率高
  - 缺点：可能丢失重要信息，特别是当多数类样本分布不均匀时
- NearMiss（基于距离的启发式采样）
  - 原理：基于样本间距离选择最具代表性的多数类样本
  - 变体：
    - NearMiss-1：选择到少数类样本平均距离最小的多数类样本
    - NearMiss-2：选择到少数类样本平均距离最大的多数类样本
    - NearMiss-3：为每个少数类样本选择最近的k个多数类样本
  - 优点：保留边界信息，提高分类效果
- Tomek Links（移除边界模糊样本）
  - 原理：识别并移除边界附近的多数类样本
  - 定义：如果两个不同类别的样本互为最近邻，则构成Tomek Link
  - 优点：清理决策边界，提高分类器性能
  - 应用：常与其他采样方法结合使用，如SMOTE+Tomek Links
主要风险：可能丢失重要信息

过采样

Oversampling

实施方法：增加少数类样本数量
典型算法：
- 随机过采样（Random Oversampling）
  - 首先在少数类集合中随机选中一些少数类样本。
  - 然后通过复制所选样本生成样本集合。
  - 将它们添加到少数类集合中来扩大原始数据集从而得到新的少数类集合。
  - 优点：实现简单，不改变原始数据分布
  - 缺点：容易导致过拟合，因为只是简单复制样本
- SMOTE（Synthetic Minority Oversampling TEchnique）
  - 原理：在少数类样本间线性插值生成新样本
  - 具体步骤：
    1. 对每个少数类样本，找到其k个最近邻
    2. 随机选择一个最近邻
    3. 在两点之间随机插值生成新样本
  - 优点：生成多样化的新样本，避免简单复制
  - 缺点：可能生成噪声样本，特别是在类别重叠区域
- ADASYN（Adaptive Synthetic Sampling）
  - 原理：SMOTE的改进版本，自适应生成样本
  - 特点：
    - 根据样本的难分类程度动态调整生成数量
    - 难分类样本（周围多数类样本多）生成更多新样本
  - 优点：更关注难分类样本，提高分类效果
  - 缺点：计算复杂度高于SMOTE
SMOTE原理：在少数类样本间线性插值生成新样本
主要风险：可能引入噪声样本

算法层面方案

代价敏感学习：
- 为不同类别设置不同的误分类代价
- 少数类样本设置更高惩罚权重
集成方法改进：
- Balanced Random Forest
  - 原理：在每棵决策树构建时进行随机欠采样
  - 特点：每棵树使用不同的多数类样本子集
  - 优点：保持随机森林的优势，同时处理类别不平衡
- EasyEnsemble（多数类多次欠采样+集成）
  - 原理：多次随机欠采样多数类，每次训练一个基分类器
  - 特点：类似Bagging，但专门处理类别不平衡
  - 优点：简单有效，计算效率高
- RUSBoost（随机欠采样+Adaboost）
  - 原理：结合随机欠采样和Adaboost
  - 特点：在每轮迭代中进行欠采样，并更新样本权重
  - 优点：同时处理类别不平衡和难分类样本
单分类/异常检测：将少数类视为异常点检测

混合策略

SMOTE+数据清洗：
- 先使用SMOTE生成新样本
- 再用Tomek Links移除噪声样本
集成采样：
- 在集成学习每轮迭代中应用不同采样策略
- 如Bagging结合随机欠采样，或Boosting结合过采样
领域自适应：利用迁移学习处理分布差异。
- 领域自适应（Domain Adaptation）用于源领域和目标领域分布不同的情况。
- 通过特征对齐、领域判别器、对抗训练等方法缩小分布差异。
- 适用于数据分布随时间、地域、设备等变化的场景。
- 例如金融风控跨城市、医疗影像跨医院等。

评估全流程实践

评估方法选择指南

小样本场景（n<1000）：
- 优先自助法（Bootstrap）
- 次选留一交叉验证（LOOCV）
中样本场景（1000<n<10000）：
- 优先分层k折交叉验证（k=5或10）
大样本场景（n>10000）：
- 留出法+多次重复
- 分层抽样保持分布一致性

指标选择决策树

回归问题：
- 首选：Adjusted R²（模型选择）
- 辅助：MAE（业务报告）、RMSE（模型优化）
分类问题：
- 样本均衡：Accuracy+AUC
- 样本不均衡：PR曲线+F1分数
- 代价敏感：根据业务风险调整Fβ的β值

线上线下评估协同

离线评估重点：
- 模型稳定性（多次重复结果方差）
- 特征重要性分析
- 不同算法比较
在线评估重点：
- 业务指标提升（CTR、转化率等）
- 用户体验变化（停留时长、跳出率等）
- 系统性能影响（响应延迟、资源消耗）
迭代机制：建立离线指标与在线指标的映射关系，持续优化评估体系

模型评估伦理考量

公平性审计：
- 检查模型在不同子群体（年龄、性别、地域）的表现差异
- 使用均衡机会（Equal Opportunity）等公平性指标
可解释性要求：
- 高风险领域（医疗、金融）需提供决策依据
- 使用SHAP、LIME等解释技术辅助评估
偏见监控：
- 持续监测训练数据中的隐性偏见
- 建立偏见检测和缓解的评估流程

二分类评估场景

垃圾邮件识别

核心需求：最小化误判正常邮件（降低FP）
指标侧重：
- 优先优化Precision（减少正常邮件误判）
- 可接受Recall适度降低（容忍少量垃圾邮件漏判）
参数调整：在Fβ分数中设置β<1（如β=0.5）
阈值策略：提高正类判定阈值（仅当概率极高时判为垃圾邮件）

金融风控

核心需求：最小化风险客户漏判（降低FN）
指标侧重：
- 优先优化Recall（确保高风险客户全捕获）
- 可接受Precision适度降低（后续人工复核可弥补）
参数调整：在Fβ分数中设置β>1（如β=2）
阈值策略：降低正类判定阈值（扩大高风险客户覆盖范围）

医疗诊断

核心需求：平衡误诊和漏诊风险
指标侧重：
- 根据不同疾病类型调整策略
- 重大疾病（如癌症）：优先Recall（避免漏诊）
- 慢性疾病：平衡Precision和Recall（F1分数）
决策考量：
- 误诊成本（不必要的治疗）
- 漏诊成本（延误治疗时机）

秋月春风

明月守灯寻长梦，梦长寻灯守月明

明月守灯寻长梦，梦长寻灯守月明

秋月春风

基本概念

离线与在线实验方法

离线实验方法

在线实验方法

对应评估指标

方法论

留出法

交叉验证法

自助法

回归问题评估指标体系

平均绝对误差（MAE）

平均绝对百分误差（MAPE）

均方误差（MSE）

均方根误差（RMSE）

决定系数（R²）

校正决定系数（Adjusted R²）

适用场景

分类问题评估指标体系

混淆矩阵（Confusion Matrix）

准确率（Accuracy）

精确率/查准率（Precision）

召回率/查全率（Recall）

Fβ分数（Fβ-Score）

ROC曲线

AUC

PR曲线

样本不均衡解决方案

数据采样技术

欠采样

过采样

算法层面方案

混合策略

评估全流程实践

评估方法选择指南

指标选择决策树

线上线下评估协同

模型评估伦理考量

二分类评估场景

垃圾邮件识别

金融风控

医疗诊断