机器学习聚类算法

• 参考：https://www.showmeai.tech/

无监督学习（Unsupervised Learning）：训练集没有标记信息，学习方式有聚类和降维。

聚类概念

聚类（Clustering）是最常见的无监督学习算法，它指的是按照某个特定标准（如距离）把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。

基本概念

1. 簇（Cluster）：一组相似的数据对象的集合

2. 相似度（Similarity）：衡量两个数据对象相似程度的度量

   • 欧氏距离（Euclidean Distance）：$d(x,y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}$
   • 曼哈顿距离（Manhattan Distance）：$d(x,y) = \sum_{i=1}^n |x_i - y_i|$
   • 余弦相似度（Cosine Similarity）：$cos(\theta) = \frac{x \cdot y}{||x|| ||y||}$

3. 聚类质量评估

   • 簇内距离（Intra-cluster Distance）：簇内所有点到簇中心的平均距离
   • 簇间距离（Inter-cluster Distance）：不同簇中心之间的距离
   • 轮廓系数（Silhouette Coefficient）：衡量簇的紧密度和分离度

聚类与分类的区别

• 聚类是一种无监督学习，而分类是一种监督的学习
• 聚类只需要人工指定相似度的标准和类别数就可以，而分类需要从训练集学习分类的方法
• 聚类用于发现数据的自然分组，分类用于预测新数据的类别

聚类算法

聚类算法应用非常广泛，包括：

• 探索性数据挖掘
• 统计分析
• 生物信息学
• 数据压缩
• 计算机图像识别
• 医学影像分析
• 市场研究
• 商品归类
• 犯罪区域分析等

主流的聚类算法可以分为两类：

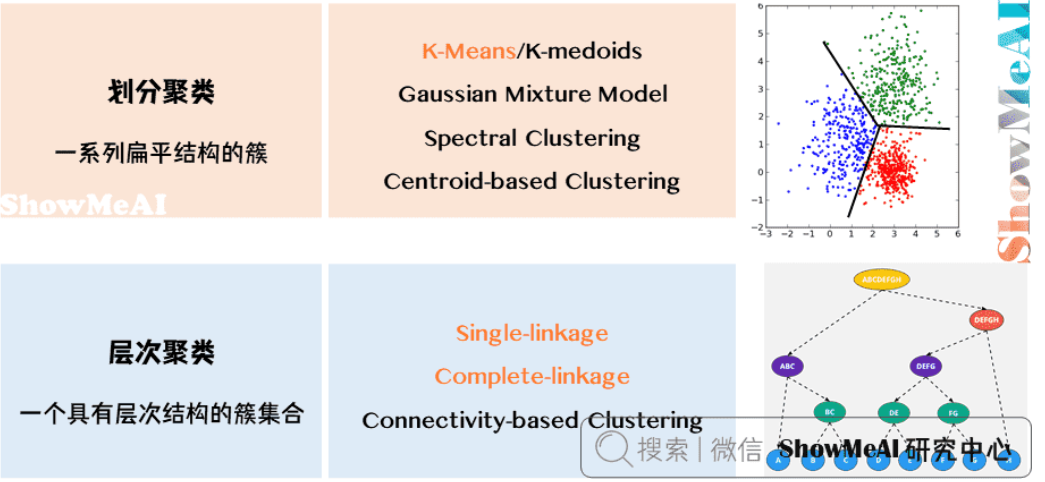
1. 划分聚类（Partitioning Clustering）

   • 特点：给出一系列扁平结构的簇，它们之间没有显式结构
   • 得到划分清晰的几个类
   • 常见算法：K-Means、K-Medoids、Gaussian Mixture Model、Spectral Clustering等

2. 层次聚类（Hierarchical Clustering）

   • 特点：输出具有层次结构的簇集合，提供更丰富的信息
   • 得到树状层次化结构
   • 常见算法：Single-linkage、Complete-linkage、Connectivity-based Clustering等

划分聚类

K-Means

核心概念

K-Means算法的目标：

• 将n个数据点分成k类
• 找到k个中心点
• 确定每个数据点属于哪个中心点

核心条件：

• 所有数据点到聚类中心的距离之和最小
• 每个数据点属于离它最近的中心点

数学原理

K-Means算法的目标函数：
$$J = \sum_{i=1}^k \sum_{x \in C_i} ||x - \mu_i||^2$$

其中：

• $C_i$ 是第i个簇
• $\mu_i$ 是第i个簇的中心点
• $||x - \mu_i||^2$ 是数据点x到中心点$\mu_i$的欧氏距离的平方

算法步骤

K-Means采用EM算法迭代确定中心点：

1. 更新中心点：

   • 初始化时随机取点作为起始点
   • 迭代过程中，取同一类所有数据点的重心作为新中心点
   • 中心点计算公式：$\mu_i = \frac{1}{|C_i|} \sum_{x \in C_i} x$

2. 分配数据点：

   • 把所有数据点分配到离它最近的中心点
   • 分配规则：$C_i = {x : ||x - \mu_i|| \leq ||x - \mu_j||, \forall j \neq i}$

重复以上步骤直到中心点不再改变。

复杂度分析

• 时间复杂度：O(n * k * i * d)
  • n：数据点数量
  • k：簇的数量
  • i：迭代次数
  • d：数据维度
• 空间复杂度：O(n * d)

特点

优点

1. 算法简单，易于实现
2. 收敛速度快
3. 适合处理大规模数据集

缺点

1. 中心点可能不属于数据集的样本点
2. 对离群点敏感，噪声和离群点会影响中心点位置
3. 需要预先指定簇的数量k
4. 对初始中心点的选择敏感
5. 只能处理凸形簇

K-Means vs KNN

K-Means和KNN（K-近邻）虽然名字相似，但它们是两个完全不同的算法：

1. 学习方式

   • K-Means：无监督学习算法
   • KNN：监督学习算法

2. 工作原理

   • K-Means：
     • 通过迭代优化找到数据的最佳聚类中心
     • 将数据点分配到最近的中心点
     • 不需要训练数据，直接对数据进行聚类
   • KNN：
     • 基于已标记的训练数据进行分类
     • 通过计算待分类点与训练集中所有点的距离
     • 选择K个最近邻的多数类别作为预测结果

3. 参数K的含义

   • K-Means：K表示聚类的数量，即要划分的簇数
   • KNN：K表示用于投票的最近邻数量

4. 计算过程

   • K-Means：
     • 需要多次迭代
     • 每次迭代都更新中心点位置
     • 直到收敛或达到最大迭代次数
   • KNN：
     • 不需要训练过程
     • 每次预测都需要计算与所有训练样本的距离
     • 直接基于距离进行投票

5. 应用场景

   • K-Means：
     • 数据聚类
     • 图像分割
     • 市场细分
     • 异常检测
   • KNN：
     • 分类问题
     • 回归问题
     • 推荐系统
     • 模式识别

代码示例

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 生成示例数据
np.random.seed(42)
X = np.random.randn(300, 2)

# 创建KMeans模型
kmeans = KMeans(n_clusters=3, random_state=42)

# 训练模型
kmeans.fit(X)

# 获取聚类结果
labels = kmeans.labels_
centers = kmeans.cluster_centers_

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, linewidths=3)
plt.title('K-Means Clustering Results')
plt.show()

K-Medoids

算法改进

针对K-Means的缺点，K-Medoids做了以下改进：

1. 限制聚类中心点必须来自数据点(K-Means的中心点可能是质心，不在数据点里)
2. 使用L1距离代替L2距离，减少对离群点的敏感度
3. 新的中心点是同一类别中离其他点最近的点

数学原理

K-Medoids的目标函数：
$$J = \sum_{i=1}^k \sum_{x \in C_i} |x - m_i|$$

其中：

• $m_i$ 是第i个簇的medoid（中心点）
• $|x - m_i|$ 是数据点x到medoid的曼哈顿距离

算法步骤

1. 随机选择k个数据点作为初始medoids
2. 将每个数据点分配到最近的medoid
3. 对每个簇，计算所有点到当前medoid的总距离
4. 尝试用簇中的其他点替换medoid，如果总距离减小则更新medoid
5. 重复步骤2-4直到medoids不再改变

复杂度分析

• 时间复杂度：O(n² * k * i)
  • n：数据点数量
  • k：簇的数量
  • i：迭代次数
• 空间复杂度：O(n * d)

代码示例

from sklearn_extra.cluster import KMedoids
import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
np.random.seed(42)
X = np.random.randn(300, 2)

# 创建KMedoids模型
kmedoids = KMedoids(n_clusters=3, random_state=42)

# 训练模型
kmedoids.fit(X)

# 获取聚类结果
labels = kmedoids.labels_
medoids = kmedoids.cluster_centers_

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.scatter(medoids[:, 0], medoids[:, 1], c='red', marker='x', s=200, linewidths=3)
plt.title('K-Medoids Clustering Results')
plt.show()

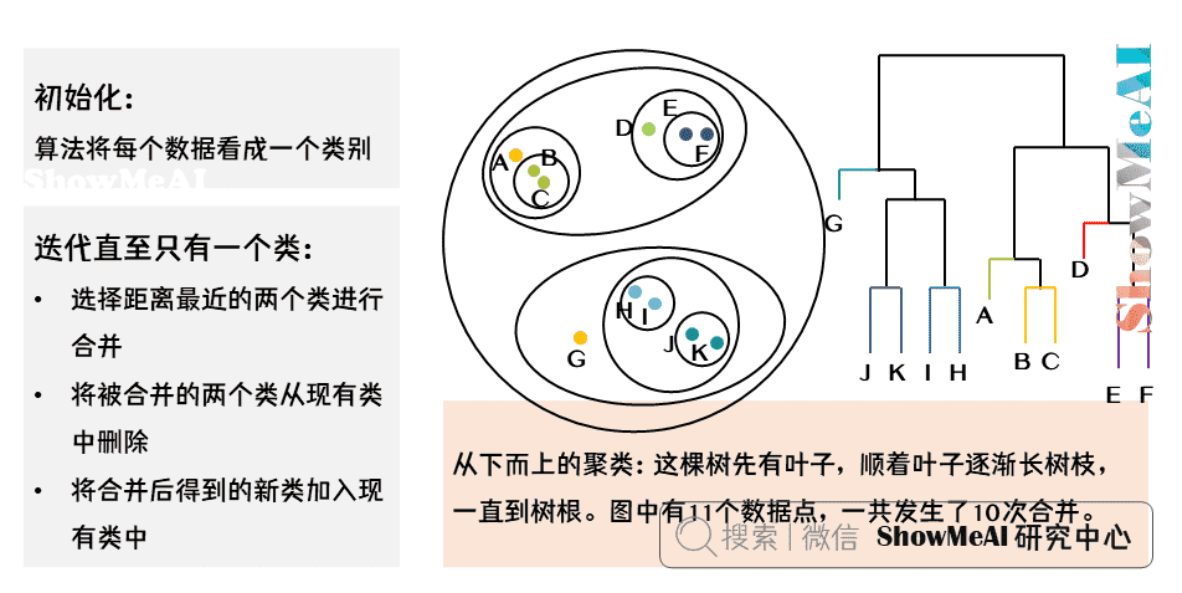
层次聚类

层次聚类（Hierarchical Clustering）是一种自底向上或自顶向下的聚类方法，它不需要预先指定簇的数量，而是通过构建一个层次化的聚类树（树状图）来展示数据的层次结构。

层次聚类最终会形成一个包含所有样本的大簇，但这个过程是渐进的，我们可以通过”截断”树状图在任意层次获得不同数量的簇。

1. 初始化：每个样本点作为一个独立的簇
2. 迭代合并：
   • 计算所有簇对之间的距离
   • 合并距离最近的两个簇
   • 更新新簇与其他簇的距离
3. 终止条件：所有样本点合并为一个簇

Single-Linkage

算法原理

Single-Linkage（单链接）算法是一种自底向上的层次聚类方法，使用两个簇中最近的两个点之间的距离作为簇间距离。

数学定义

簇间距离：
$$d(C_i, C_j) = \min_{x \in C_i, y \in C_j} d(x,y)$$

其中：

• $C_i, C_j$ 是两个簇
• $d(x,y)$ 是点x和点y之间的距离

算法步骤

1. 将每个数据点视为一个簇
2. 计算所有簇对之间的距离
3. 合并距离最小的两个簇
4. 更新新簇与其他簇的距离
5. 重复步骤2-4直到只剩下一个簇

复杂度分析

• 时间复杂度：O(n² * log n)
• 空间复杂度：O(n²)

代码示例

from scipy.cluster.hierarchy import linkage, dendrogram
import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
np.random.seed(42)
X = np.random.randn(30, 2)

# 计算层次聚类
Z = linkage(X, method='single')

# 绘制树状图
plt.figure(figsize=(10, 7))
dendrogram(Z)
plt.title('Single-Linkage Hierarchical Clustering')
plt.show()

Complete-Linkage

算法原理

Complete-Linkage（完全链接）算法使用两个簇中最远的两个点之间的距离作为簇间距离。

数学定义

簇间距离：
$$d(C_i, C_j) = \max_{x \in C_i, y \in C_j} d(x,y)$$

算法步骤

与Single-Linkage类似，但使用最大距离而不是最小距离。

复杂度分析

• 时间复杂度：O(n² * log n)
• 空间复杂度：O(n²)

代码示例

from scipy.cluster.hierarchy import linkage, dendrogram
import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
np.random.seed(42)
X = np.random.randn(30, 2)

# 计算层次聚类
Z = linkage(X, method='complete')

# 绘制树状图
plt.figure(figsize=(10, 7))
dendrogram(Z)
plt.title('Complete-Linkage Hierarchical Clustering')
plt.show()

密度聚类

DB-SCAN

DB-SCAN 是一个基于密度的聚类。如下图中这样不规则形态的点，如果用 K-Means，效果不会很好。而通过 DB-SCAN 就可以很好地把在同一密度区域的点聚在一类中。

算法特点

• 基于密度的聚类算法
• 适合处理不规则形态的数据
• 不需要预先指定聚类数量
• 可以发现任意形状的簇
• 能够识别噪声点

核心概念

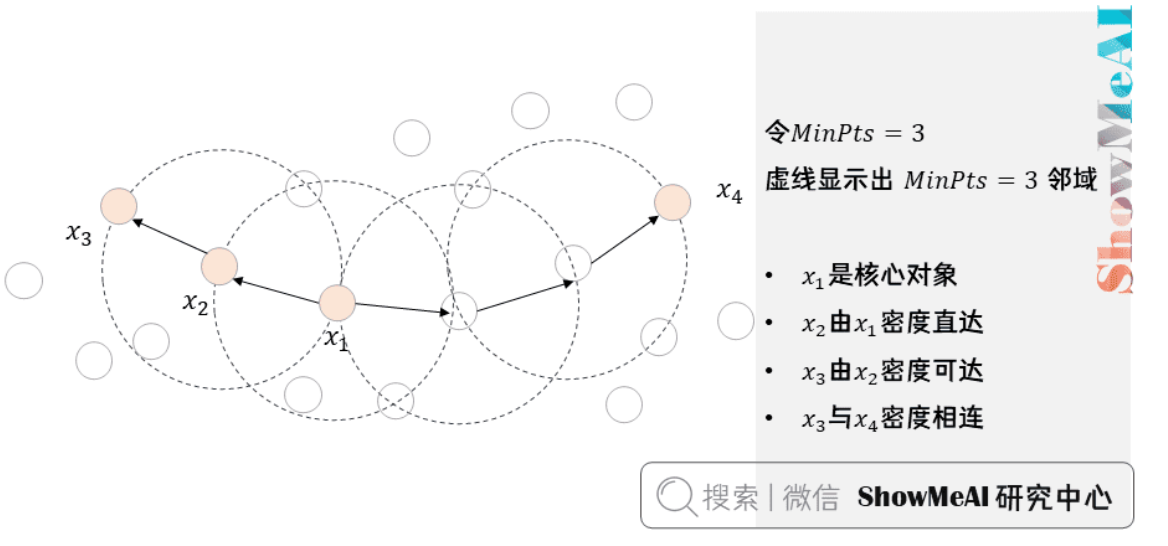
1. 核心对象（Core Object）

   • 密度达到一定程度的点
   • ε邻域内至少包含MinPts个样本
   • 数学定义：$N_\epsilon(p) = {q \in D | d(p,q) \leq \epsilon}$
   • 如果$|N_\epsilon(p)| \geq MinPts$，则p是核心对象

2. 密度关系

   • 密度直达：点位于核心对象的ε邻域中
   • 密度可达：通过一系列密度直达关系连接
   • 密度相连：两个点都可由某个点密度可达

算法步骤

1. 设定参数：MinPts（最小点密度）和ε（半径范围）
2. 找出所有核心对象
3. 随机选择一个核心对象，找出所有密度可达的点
4. 重复步骤3直到所有点都被处理

复杂度分析

• 时间复杂度：O(n²)，使用空间索引可以优化到O(n log n)
• 空间复杂度：O(n)

代码示例

from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
np.random.seed(42)
X = np.random.randn(300, 2)

# 创建DBSCAN模型
dbscan = DBSCAN(eps=0.3, min_samples=5)

# 训练模型
dbscan.fit(X)

# 获取聚类结果
labels = dbscan.labels_

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.title('DBSCAN Clustering Results')
plt.show()

优缺点分析

优点：

1. 不需要预先指定簇的数量
2. 可以发现任意形状的簇
3. 能够识别噪声点
4. 只需要两个参数：ε和MinPts

缺点：

1. 对参数敏感
2. 不适合处理高维数据
3. 对数据密度不均匀的情况效果不好
4. 计算复杂度较高