机器学习降维算法

• 参考：https://www.showmeai.tech/

无监督学习（Unsupervised Learning）：训练集没有标记信息，学习方式有聚类和降维。

降维概念

在数据挖掘和建模的过程中，高维数据会带来大的计算量，占据更多的资源，而且许多变量之间可能存在相关性，从而增加了分析与建模的复杂性。

降维的目标是在对数据完成降维「压缩」的同时，尽量减少信息损失。由于各变量之间存在一定的相关关系，因此可以考虑将关系紧密的变量变成尽可能少的新变量，使这些新变量是两两不相关的，那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。

主成分分析(PCA)

基本概念

主成分分析（Principal Components Analysis，简称PCA）是最重要的数据降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。

数学原理

最大可分性

对于n维数据，我们希望将其降到k维，同时希望信息损失最少。PCA的目标是找到k个投影方向，使得数据在这些方向上的投影方差最大。

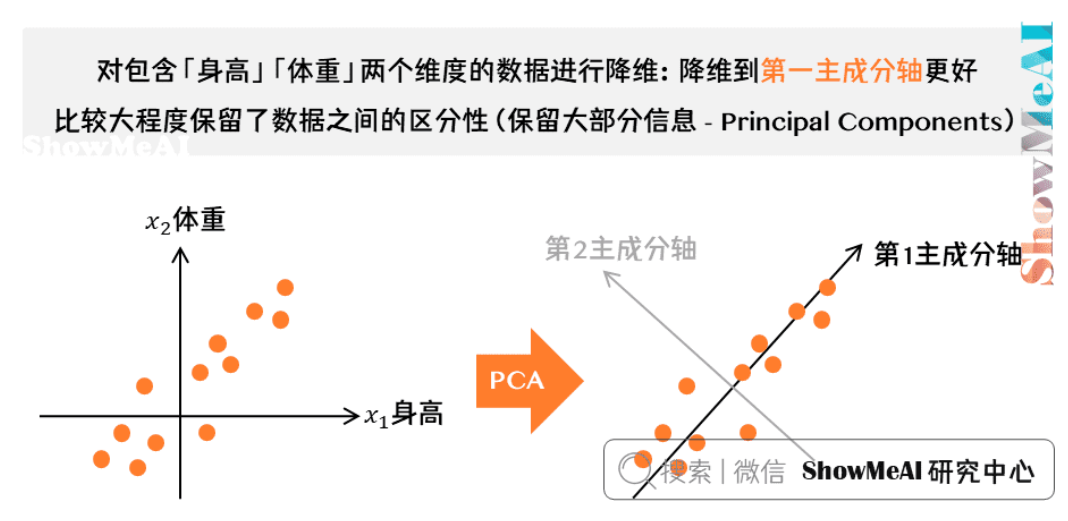
基变换

原始数据X通过线性变换得到新的表示空间Y：
$$Y = PX$$

其中：

• X是原始样本
• P是基向量矩阵
• Y是新表达

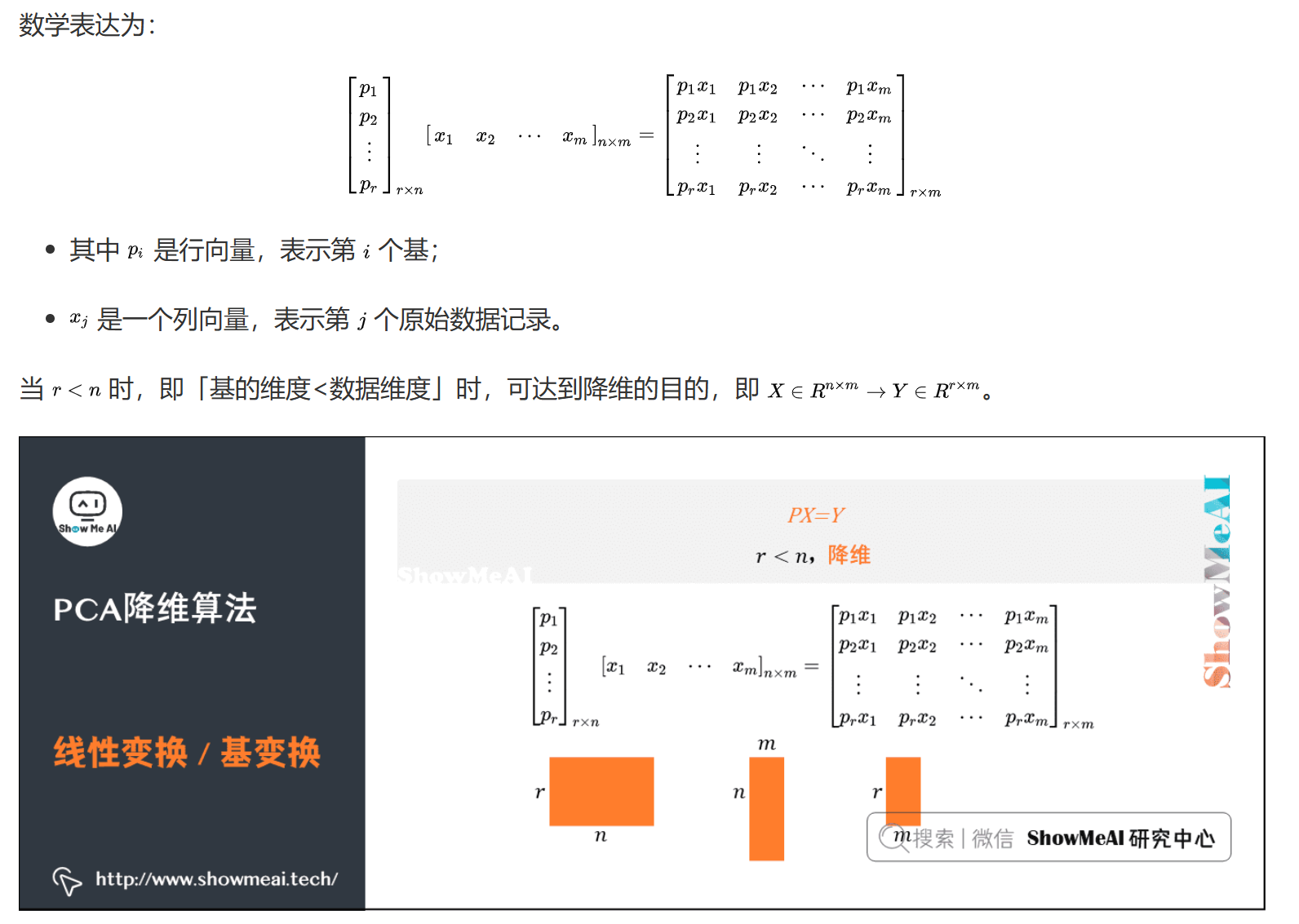
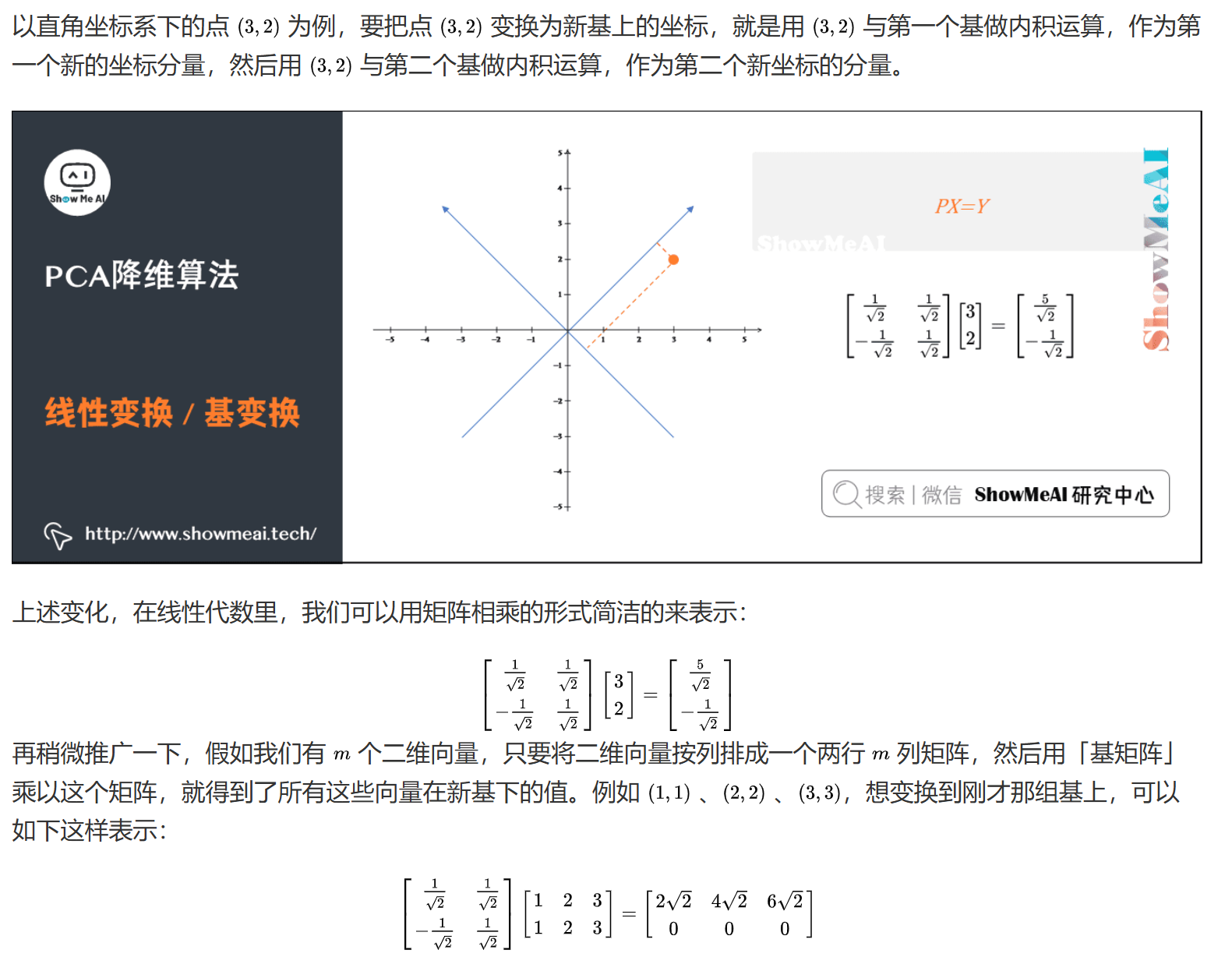
方差与协方差

1. 方差：衡量数据的分散程度
   $$Var(X) = \frac{1}{n}\sum_{i=1}^n (x_i - \mu)^2$$

2. 协方差：衡量两个变量的总体误差
   $$Cov(X,Y) = \frac{1}{n}\sum_{i=1}^n (x_i - \mu_x)(y_i - \mu_y)$$

3. 协方差矩阵：
   $$C = \frac{1}{m}XX^T$$

协方差矩阵对角化

算法步骤

核心思路

PCA的核心是找到协方差矩阵的特征向量，这些特征向量就是我们需要的主成分方向。具体步骤：

1. 计算协方差矩阵C
2. 计算C的特征值和特征向量
3. 将特征向量按特征值大小排序
4. 取前k个特征向量组成投影矩阵P

详细步骤

1. 数据预处理

   • 将原始数据按列组成n行m列矩阵X
   • 对每一行（每个特征）进行零均值化处理：
     $$x_{ij} = x_{ij} - \mu_j$$
     其中$\mu_j$是第j个特征的均值

2. 计算协方差矩阵

   • 计算中心化后的数据的协方差矩阵：
     $$C = \frac{1}{m}XX^T$$
   • 协方差矩阵C是一个m×m的对称矩阵
   • 对角线元素表示各个特征的方差
   • 非对角线元素表示不同特征之间的协方差

3. 特征值分解

   • 对协方差矩阵C进行特征值分解：
     $$C = Q\Lambda Q^T$$
   • 其中：
     • Q是特征向量矩阵，每一列是一个特征向量
     • $\Lambda$是对角矩阵，对角线上的元素是特征值
   • 特征值表示对应特征向量的方差贡献

4. 特征向量排序

   • 将特征值从大到小排序
   • 对应的特征向量也相应排序
   • 排序后的特征向量构成了主成分方向
   • 特征值的大小反映了对应主成分的重要性

5. 选择主成分

   • 根据需求选择前k个主成分
   • 可以通过以下方式确定k：
     1. 指定降维后的维度k
     2. 指定信息保留率$\eta$：
        $$\eta = \frac{\sum_{i=1}^k \lambda_i}{\sum_{i=1}^m \lambda_i} \geq \eta_{target}$$
     3. 观察特征值的”拐点”（碎石图）

6. 构建投影矩阵

   • 取前k个特征向量组成投影矩阵P
   • P是一个k×m的矩阵
   • 每一行是一个主成分方向

7. 数据降维

   • 将原始数据投影到新的空间：
     $$Y = PX$$
   • Y是降维后的数据，维度为k×n
   • 每一行代表一个主成分
   • 每一列代表一个样本

8. 结果解释

   • 计算每个主成分的贡献率：
     $$contribution_i = \frac{\lambda_i}{\sum_{j=1}^m \lambda_j}$$
   • 计算累计贡献率：
     $$cumulative_i = \sum_{j=1}^i contribution_j$$
   • 分析主成分的实际含义
   • 评估降维效果

特点

优点：

1. 可以降低数据维度，减少计算量
2. 可以去除数据中的噪声
3. 可以提取数据的主要特征

缺点：

1. 只能处理线性关系
2. 对异常值敏感
3. 需要预先指定降维维度

代码实现

import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 生成示例数据
X = np.random.randn(1000, 3)

# 创建PCA模型
pca = PCA(n_components=2)

# 训练模型
pca.fit(X)

# 降维
X_new = pca.transform(X)

# 可视化结果
plt.scatter(X_new[:, 0], X_new[:, 1])
plt.title('PCA降维结果')
plt.show()

# 查看方差解释率
print("方差解释率：", pca.explained_variance_ratio_)

线性判别分析（LDA）

基本概念

线性判别分析（Linear Discriminant Analysis，简称LDA）是一种有监督的降维方法，它试图找到能够最大化类间距离同时最小化类内距离的投影方向。

数学原理

类内散度矩阵

类内散度矩阵（Within-class Scatter Matrix）衡量每个类别内部样本的分散程度：

$$S_w = \sum_{i=1}^c \sum_{x \in X_i} (x - \mu_i)(x - \mu_i)^T$$

其中：

• c是类别数
• $X_i$是第i类的样本集合
• $\mu_i$是第i类的均值向量

类间散度矩阵

类间散度矩阵（Between-class Scatter Matrix）衡量不同类别之间的分散程度：

$$S_b = \sum_{i=1}^c N_i(\mu_i - \mu)(\mu_i - \mu)^T$$

其中：

• $N_i$是第i类的样本数
• $\mu$是所有样本的均值向量

目标函数推导

LDA的目标是找到一个投影方向w，使得：

1. 类间距离最大化
2. 类内距离最小化

这可以转化为以下优化问题：

$$\max_w J(w) = \frac{w^TS_bw}{w^TS_ww}$$

使用拉格朗日乘子法求解：

$$L(w, \lambda) = w^TS_bw - \lambda(w^TS_ww - 1)$$

对w求导并令其等于0：

$$\frac{\partial L}{\partial w} = 2S_bw - 2\lambda S_ww = 0$$

整理得到：

$$S_bw = \lambda S_ww$$

这是一个广义特征值问题，可以通过求解$S_w^{-1}S_b$的特征值和特征向量得到最优投影方向。

算法步骤

1. 数据预处理

   • 计算每个类别的均值向量
   • 计算总体均值向量

2. 计算散度矩阵

   • 计算类内散度矩阵Sw
   • 计算类间散度矩阵Sb

3. 特征值分解

   • 计算$S_w^{-1}S_b$的特征值和特征向量
   • 将特征值从大到小排序

4. 选择投影方向

   • 选择前k个最大特征值对应的特征向量
   • 组成投影矩阵W

5. 数据降维

   • 将原始数据投影到新的空间：Y = WX

特点

优点：

1. 考虑了类别信息
2. 可以处理多分类问题
3. 降维后类别可分性更好

缺点：

1. 只能处理线性关系
2. 需要类别标签
3. 对异常值敏感

代码实现

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# 创建LDA模型
lda = LinearDiscriminantAnalysis(n_components=2)

# 训练模型
lda.fit(X, y)

# 降维
X_new = lda.transform(X)

# 可视化结果
plt.scatter(X_new[:, 0], X_new[:, 1], c=y)
plt.title('LDA降维结果')
plt.show()

UMAP

Uniform Manifold Approximation and Projection

基本概念

UMAP是一种非线性降维算法，它基于黎曼几何和代数拓扑的理论，能够保持数据的局部和全局结构。相比t-SNE，UMAP具有更快的计算速度和更好的可扩展性。

数学原理

高维空间中的相似度

UMAP首先在高维空间中构建一个模糊拓扑结构：

1. 局部距离计算

   • 对每个点找到k个最近邻
   • 计算局部距离度量
   • 使用局部距离构建局部连通性

2. 模糊集构建

   • 使用指数函数将距离转换为相似度：
     $$p_{ij} = \exp(-\frac{d(x_i, x_j) - \rho_i}{\sigma_i})$$
     其中：
   • $d(x_i, x_j)$是点i和j之间的距离
   • $\rho_i$是点i到其最近邻的距离
   • $\sigma_i$是局部尺度参数

低维空间中的相似度

在低维空间中，使用以下函数计算相似度：

$$q_{ij} = (1 + a(y_i - y_j)^{2b})^{-1}$$

其中：

• a和b是超参数，控制低维嵌入的紧密程度
• 这个函数形式可以更好地保持数据的全局结构

目标函数

使用交叉熵作为损失函数：

$$L = \sum_{i,j} p_{ij} \log(\frac{p_{ij}}{q_{ij}}) + (1-p_{ij})\log(\frac{1-p_{ij}}{1-q_{ij}})$$

优化过程

使用随机梯度下降进行优化：

1. 初始化

   • 使用谱嵌入或随机初始化
   • 可以保持局部结构

2. 梯度计算

   • 计算损失函数对低维坐标的梯度
   • 使用负采样加速计算

3. 参数更新

   • 使用带动量的随机梯度下降
   • 可以设置学习率衰减

算法步骤

1. 数据预处理

   • 计算k近邻图
   • 确定局部尺度参数
   • 构建模糊拓扑结构

2. 初始化低维空间

   • 使用谱嵌入或随机初始化
   • 保持局部结构

3. 优化过程

   • 计算高维和低维相似度
   • 计算梯度
   • 更新低维坐标
   • 使用早停策略

4. 结果后处理

   • 可选的数据标准化
   • 结果可视化

特点

优点：

1. 计算速度快
2. 可以处理大规模数据
3. 保持数据的局部和全局结构
4. 内存效率高
5. 可以处理各种类型的数据

缺点：

1. 需要调整超参数
2. 对噪声敏感
3. 结果可能不稳定
4. 需要较大的k值

代码实现

import umap
import numpy as np
import matplotlib.pyplot as plt

# 创建UMAP模型
reducer = umap.UMAP(
    n_neighbors=15,          # 局部连通性参数
    min_dist=0.1,           # 控制点之间的最小距离
    n_components=2,         # 降维后的维度
    metric='euclidean',     # 距离度量方式
    random_state=42
)

# 训练模型并降维
X_new = reducer.fit_transform(X)

# 可视化结果
plt.scatter(X_new[:, 0], X_new[:, 1], c=y)
plt.title('UMAP降维结果')
plt.show()

# 查看模型参数
print("学习率：", reducer.learning_rate)
print("局部连通性：", reducer.n_neighbors)

参数调优

1. n_neighbors

   • 控制局部结构的粒度
   • 较小的值保持更局部的结构
   • 较大的值保持更全局的结构
   • 建议范围：5-50

2. min_dist

   • 控制点之间的最小距离
   • 较小的值产生更紧密的聚类
   • 较大的值产生更分散的分布
   • 建议范围：0.0-0.99

3. n_components

   • 降维后的维度
   • 通常设置为2或3用于可视化
   • 可以根据需要设置更高维度

4. metric

   • 距离度量方式
   • 常用选项：’euclidean’, ‘manhattan’, ‘cosine’
   • 可以根据数据类型选择

应用场景

1. 数据可视化

   • 高维数据的2D/3D可视化
   • 数据分布探索
   • 异常检测

2. 特征提取

   • 降维后的特征可用于后续任务
   • 可以保持数据的语义信息

3. 数据预处理

   • 用于其他机器学习算法的预处理
   • 减少计算复杂度

4. 生物信息学

   • 基因表达数据分析
   • 单细胞RNA测序数据

t-SNE

t-Distributed Stochastic Neighbor Embedding

基本概念

t-SNE是一种非线性降维算法，特别适合用于可视化高维数据。它通过保持数据点之间的相似关系，将高维数据映射到低维空间。t-SNE的核心思想是：在高维空间中相似的点在低维空间中应该保持相似，而不相似的点应该保持距离。

数学原理

高维空间中的相似度

在原始高维空间中，使用高斯分布计算点对之间的相似度：

$$p_{j|i} = \frac{\exp(-||x_i - x_j||^2/2\sigma_i^2)}{\sum_{k \neq i} \exp(-||x_i - x_k||^2/2\sigma_i^2)}$$

其中：

• $\sigma_i$是第i个点的带宽参数
• 通过二分搜索确定，使得困惑度（perplexity）达到指定值
• 困惑度反映了局部邻居的数量

低维空间中的相似度

在低维空间中，使用t分布计算点对之间的相似度：

$$q_{ij} = \frac{(1 + ||y_i - y_j||^2)^{-1}}{\sum_{k \neq l} (1 + ||y_k - y_l||^2)^{-1}}$$

使用t分布而不是高斯分布的原因是：

1. t分布有更重的尾部，可以更好地保持数据的局部结构
2. 可以避免”拥挤问题”（crowding problem）
3. 有助于保持全局结构

目标函数

使用KL散度衡量两个分布之间的差异：

$$C = KL(P||Q) = \sum_i \sum_j p_{ij} \log \frac{p_{ij}}{q_{ij}}$$

梯度下降优化

目标函数对低维空间中的点求导：

$$\frac{\partial C}{\partial y_i} = 4\sum_j (p_{ij} - q_{ij})(y_i - y_j)(1 + ||y_i - y_j||^2)^{-1}$$

使用梯度下降更新低维空间中的点：

$$y_i^{(t+1)} = y_i^{(t)} - \eta \frac{\partial C}{\partial y_i} + \alpha(t)(y_i^{(t)} - y_i^{(t-1)})$$

其中：

• $\eta$是学习率
• $\alpha(t)$是动量项

算法步骤

1. 计算高维相似度

   • 对每个点计算带宽参数
   • 计算条件概率$p_{j|i}$
   • 计算联合概率$p_{ij} = \frac{p_{j|i} + p_{i|j}}{2n}$

2. 初始化低维空间

   • 随机初始化低维空间中的点
   • 通常使用较小的随机值
   • 可以设置随机种子

3. 迭代优化

   • 计算低维空间中的相似度$q_{ij}$
   • 计算梯度
   • 更新低维空间中的点
   • 使用早停策略

4. 结果可视化

   • 将最终的低维表示可视化
   • 可以使用不同的颜色表示不同的类别

特点

优点：

1. 可以保持数据的局部结构
2. 适合可视化
3. 可以处理非线性关系
4. 对异常值不敏感
5. 结果直观易懂

缺点：

1. 计算复杂度高
2. 结果不稳定
3. 需要调整参数
4. 不适合大规模数据
5. 内存消耗大

代码实现

from sklearn.manifold import TSNE
import numpy as np
import matplotlib.pyplot as plt

# 创建t-SNE模型
tsne = TSNE(
    n_components=2,          # 降维后的维度
    perplexity=30.0,        # 困惑度参数
    n_iter=1000,            # 迭代次数
    learning_rate='auto',   # 学习率
    random_state=42         # 随机种子
)

# 降维
X_new = tsne.fit_transform(X)

# 可视化结果
plt.scatter(X_new[:, 0], X_new[:, 1], c=y)
plt.title('t-SNE降维结果')
plt.show()

# 查看模型参数
print("最终困惑度：", tsne.perplexity_)
print("最终KL散度：", tsne.kl_divergence_)

参数调优

1. perplexity

   • 控制局部邻居的数量
   • 较小的值产生更局部的结构
   • 较大的值产生更全局的结构
   • 建议范围：5-50

2. n_iter

   • 迭代次数
   • 较小的值可能未收敛
   • 较大的值计算时间长
   • 建议范围：250-1000

3. learning_rate

   • 学习率
   • 较小的值收敛慢
   • 较大的值可能不稳定
   • 可以使用’auto’自动选择

4. n_components

   • 降维后的维度
   • 通常设置为2或3用于可视化
   • 可以根据需要设置更高维度

应用场景

1. 数据可视化

   • 高维数据的2D/3D可视化
   • 数据分布探索
   • 异常检测

2. 特征提取

   • 降维后的特征可用于后续任务
   • 可以保持数据的语义信息

3. 数据预处理

   • 用于其他机器学习算法的预处理
   • 减少计算复杂度

4. 生物信息学

   • 基因表达数据分析
   • 单细胞RNA测序数据

t-SNE vs UMAP

对比维度	t-SNE	UMAP
理论基础	基于概率分布和KL散度	基于黎曼几何和代数拓扑
计算效率	计算复杂度高，内存消耗大	计算速度快，内存效率高
可扩展性	不适合大规模数据	可以处理大规模数据
参数敏感性	对参数更敏感	参数调整更灵活
结果稳定性	结果可能不稳定	结果相对更稳定
局部/全局结构	更注重局部结构	同时保持局部和全局结构
相似度计算	高维：高斯分布 低维：t分布	高维：指数函数 低维：幂函数
优化方法	梯度下降	随机梯度下降
初始化方式	随机初始化或PCA	谱嵌入或随机初始化
收敛速度	较慢	较快
内存占用	较大	较小
并行计算	支持有限	支持良好
参数数量	较少	较多
可视化效果	局部结构清晰	全局结构更完整

选择建议

场景	推荐算法	原因
数据规模	小规模数据	两种方法都可以
	大规模数据	优先选择UMAP
计算资源	资源有限	选择UMAP
	资源充足	两种方法都可以
可视化需求	注重局部结构	选择t-SNE
	需要全局结构	选择UMAP
稳定性要求	需要稳定结果	选择UMAP
	可以接受随机性	两种方法都可以
实时性要求	需要快速结果	选择UMAP
	可以等待	两种方法都可以
内存限制	内存有限	选择UMAP
	内存充足	两种方法都可以

自编码器（Autoencoder）

基本概念

自编码器是一种神经网络，它通过无监督学习的方式，将输入数据压缩到低维空间，然后再重建回原始空间。

网络结构

编码器

编码器将输入数据压缩到低维空间：

$$h = f(W_1x + b_1)$$

其中：

• $W_1$是权重矩阵
• $b_1$是偏置向量
• f是激活函数（如ReLU、sigmoid等）

解码器

解码器将低维表示重建回原始空间：

$$\hat{x} = g(W_2h + b_2)$$

其中：

• $W_2$是权重矩阵
• $b_2$是偏置向量
• g是激活函数

目标函数

自编码器的目标是最小化重建误差：

$$L = \frac{1}{n}\sum_{i=1}^n ||x_i - \hat{x}_i||^2$$

对于二值数据，可以使用交叉熵损失：

$$L = -\frac{1}{n}\sum_{i=1}^n [x_i \log \hat{x}_i + (1-x_i)\log(1-\hat{x}_i)]$$

训练过程

1. 前向传播

   • 输入数据通过编码器得到低维表示
   • 低维表示通过解码器得到重建结果

2. 反向传播

   • 计算重建误差
   • 计算梯度
   • 更新网络参数

3. 正则化

   • 可以使用L1/L2正则化
   • 可以使用Dropout
   • 可以使用稀疏约束

特点

优点：

1. 可以学习非线性特征
2. 可以处理大规模数据
3. 可以用于特征提取

缺点：

1. 需要大量训练数据
2. 训练时间长
3. 结果可能不稳定

代码实现

import tensorflow as tf
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.models import Model

# 定义编码器
input_dim = X.shape[1]
encoding_dim = 2

input_layer = Input(shape=(input_dim,))
encoded = Dense(encoding_dim, activation='relu')(input_layer)
decoded = Dense(input_dim, activation='sigmoid')(encoded)

# 创建自编码器模型
autoencoder = Model(input_layer, decoded)

# 编译模型
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

# 训练模型
autoencoder.fit(X, X, epochs=50, batch_size=32, shuffle=True)

# 获取编码器
encoder = Model(input_layer, encoded)

# 降维
X_new = encoder.predict(X)

# 可视化结果
plt.scatter(X_new[:, 0], X_new[:, 1], c=y)
plt.title('自编码器降维结果')
plt.show()