参考：

NLP介绍

自然语言

词汇含义

人类的语言是一个专门用来表达意义的系统,语言文字是上层抽象表征。

人类语言具有以下特点:

信息功能和社会功能
只有约5000年的历史
传播速度相对较慢,但信息密度高
是离散的(discrete)、符号的(symbolic)、分类的(categorical)系统

最普遍的语言方式是语言符号与语言意义(想法、事情)的相互对应

denotational semantics(语义)：
signifier(symbol)↔signified(idea or thing)

大多数单词只是一个语言学以外的符号：单词是一个映射到所指(signified 想法或事物)的能指(signifier)。

这些语言的符号可以被编码成几种形式：声音、手势、文字等等，然后通过连续的信号传输给大脑；大脑本身似乎也能以一种连续的方式对这些信号进行解码。人们在语言哲学和语言学方面做了大量的工作来概念化人类语言，并将词语与其参照、意义等区分开来。

语言文字是上层抽象表征，NLP与计算机视觉或任何其他机器学习任务都有很大的不同。

计算机中表达词义

离散式表示

WordNet

构建包含同义词集和上位词(“is a”关系)的列表的辞典
可以通过NLTK工具库使用

from nltk.corpus import wordnet as wn
poses = { 'n':'noun', 'v':'verb', 's':'adj (s)', 'a':'adj', 'r':'adv'}
for synset in wn.synsets("good"):
        print("{}: {}".format(poses[synset.pos()], ", ".join([l.name() for l in synset.lemmas()])))
from nltk.corpus import wordnet as wn
panda = wn.synset("panda.n.01")
hyper = lambda s: s.hypernyms()
list(panda.closure(hyper))

结果示例：

存在以下问题:

忽略了词汇的细微差别

某些词义的差别，在不同语境词义变化等

缺少单词的新含义

无法随时代更新

主观性强
构建与调整需要大量人力

3 & 4都因为有人类专家参与

无法定量计算单词相似度

只有定性的关系性

one-hot

传统NLP中,我们使用离散表征:
把词语看作离散的符号，使用one-hot向量表示

独热向量：只有一个1，其余均为0的稀疏向量
向量维度等于词汇量(如500,000)

存在以下问题:

所有词向量正交,没有相似性概念
向量维度过大
稀疏性问题

有一些解决思路：
① 使用类似WordNet的工具中的列表，获得相似度，但会因不够完整而失败
② 通过大量数据学习词向量本身相似性，获得更精确的稠密词向量编码→基于SVD降维的词向量

词袋模型

Bag-of-words model

词袋模型是一种将文本表示为词频向量的方法，不考虑词的顺序和语法结构。

基本思想

将文本看作一个装着词的袋子
只关注词的出现与否和出现次数
忽略词的顺序和语法关系

具体示例

对于以下两个句子：

1 2	John likes to watch movies. Mary likes too John also likes to watch football games.

构建词典：

1	{"John": 1, "likes": 2, "to": 3, "watch": 4, "movies": 5, "also": 6, "football": 7, "games": 8, "Mary": 9, "too": 10}

向量表示：

第一句：[1,2,1,1,1,0,0,0,1,1]
- 2表示”likes”出现2次
- 1表示其他词各出现1次
- 0表示未出现的词
第二句：[1,1,1,1,0,1,1,1,0,0]

优缺点

优点：

简单直观，易于实现
计算效率高
适合文本分类等任务

缺点：

词序信息丢失
- 无法表达词的顺序关系
- 例如：”我喜欢你”和”你喜欢我”的表示相同
语义信息不完整
- 词向量化后，词与词之间的大小关系不一定合理
- 词频不一定能准确反映词的重要性

TF-IDF

Term Frequency-Inverse Document Frequency

TF-IDF是一种用于评估词语重要性的统计方法，常用于信息检索和文本挖掘。

基本概念

TF (Term Frequency)
- 词频：词语在文档中出现的次数
- 计算公式：
  $$
  \text{TF}(w,d) = \frac{f_{w,d}}{\sum_{k \in d} f_{k,d}}
  $$
  其中：
- $f_{w,d}$：词$w$在文档$d$中出现的次数
- $\sum_{k \in d} f_{k,d}$：文档$d$中所有词的出现次数之和
IDF (Inverse Document Frequency)
- 逆文档频率：衡量词语的普遍重要性
- 计算公式：
  $$
  \text{IDF}(w) = \log \frac{N}{1 + \text{DF}(w)}
  $$
  其中：
- $N$：语料库中的文档总数
- $\text{DF}(w)$：包含词$w$的文档数量
- 分母加1是为了避免分母为0
TF-IDF值
- 计算公式：
  $$
  \text{TF-IDF}(w,d) = \text{TF}(w,d) \times \text{IDF}(w)
  $$

计算示例

假设有以下三个文档：

1
2
3

文档1：The cat sat on the mat
文档2：The dog chased the cat
文档3：The mat is on the floor

计算TF值：
- 对于文档1中的”cat”：
  - 出现次数：1
  - 文档总词数：6
  - TF = 1/6 ≈ 0.167
- 对于文档1中的”the”：
  - 出现次数：2
  - 文档总词数：6
  - TF = 2/6 ≈ 0.333
计算IDF值：
- 总文档数：3
- “cat”出现在2个文档中
- IDF = log(3/(1+2)) = log(1) = 0
- “the”出现在3个文档中
- IDF = log(3/(1+3)) = log(0.75) ≈ -0.125
- “dog”出现在1个文档中
- IDF = log(3/(1+1)) = log(1.5) ≈ 0.176
计算TF-IDF值：
- 文档1中”cat”的TF-IDF = 0.167 × 0 = 0
- 文档1中”the”的TF-IDF = 0.333 × (-0.125) ≈ -0.042
- 文档2中”dog”的TF-IDF = (1/6) × 0.176 ≈ 0.029

这个例子说明：

常见词（如”the”）的TF-IDF值较低，甚至为负
中等频率词（如”cat”、”dog”）的TF-IDF值适中
真正重要的词应该是那些在特定文档中频繁出现，但在其他文档中较少出现的词

特点

优点：
- 能够反映词语在文档中的重要性
- 考虑了词语的普遍性
- 计算简单，易于实现
缺点：
- 仍然无法表达词序信息
- 没有考虑词语的语义关系
- 对短文本效果不佳

n-gram

见下文

分布式表示

核心：基于上下文

近年来在深度学习中比较有效的方式是基于上下文的词汇表征。
它的核心想法是：一个单词的意思是由经常出现在它附近的单词给出的。

“You shall know a word by the company it keeps” (J. R. Firth 1957: 11)
这是现代统计NLP最成功的理念之一(总体思路：物以类聚，人以群分)。

当一个单词w出现在文本中时，它的上下文是出现在其附近的一组单词。(在一个固定大小的窗口中)
基于海量数据，使用w的许多上下文来构建w的表示。

词向量

见下

NLP任务

简单任务

拼写检查 Spell Checking
关键词检索 Keyword Search
同义词查找 Finding Synonyms

中级任务

解析来自网站、文档等的信息

复杂任务

机器翻译 Machine Translation
语义分析 Semantic Analysis
指代消解 Coreference
问答系统 Question Answering

n-gram

基本思想

“You shall know a word by the company it keeps”

在自然语言处理中，我们希望对一个词序列 $w_1, w_2, \dots, w_n$ 的概率进行建模：

$$
P(w_1, w_2, \dots, w_n)
$$

n-gram模型假设：一个词的出现只依赖于它前面的 $n-1$ 个词。

核心目标：给定前面的词，预测下一个词出现的概率。

Unigram

假设每个词的出现是完全独立的(简单但不符合实际)：

$$
P(w_1, w_2, \dots, w_n) = \prod_{i=1}^n P(w_i)
$$

Bigram

假设每个词只依赖于前一个词(n=2)：

$$
P(w_1, w_2, \dots, w_n) = P(w_1) \prod_{i=2}^n P(w_i | w_{i-1})
$$

使用 bigram 都可以带来相对 unigram显著的提升。

Trigram

对于trigram模型(n=3)：
$$P(w_t|w_1, w_2, …, w_{t-1}) \approx P(w_t|w_{t-2}, w_{t-1})$$

n-gram

假设每个词只依赖于前 $n-1$ 个词：

$$
P(w_1, w_2, \dots, w_n) = \prod_{i=1}^n P(w_i | w_{i-(n-1)}, \dots, w_{i-1})
$$

概率估计

n-gram概率通常通过最大似然估计（MLE）从语料库中统计。

n-grams 语言模型基于 n 阶马尔可夫假设（n-th Order Markov Assumption） 和 离散型随机变量的极大似然估计（Maximum Likelihood Estimation, MLE）：

n 阶马尔可夫假设：当前词的概率只与前 n 个词有关，即 $P(w_N|w_1, w_2, \dots, w_{N-1}) \approx P(w_N|w_{N-n}, \dots, w_{N-1})$。
极大似然估计：通过最大化似然函数 $L(\theta) = \prod_{i=1}^{M} \prod_{j=1}^{M} P(w_j|w_i)^{C(w_i, w_j)}$ 来估计参数，最终得到 $P(w_j|w_i) = \frac{C(w_i, w_j)}{C(w_i)}$。

bigram：

$$
P(w_i | w_{i-1}) = \frac{\text{Count}(w_{i-1}, w_i)}{\text{Count}(w_{i-1})}
$$

trigram：

$$
P(w_i | w_{i-2}, w_{i-1}) = \frac{\text{Count}(w_{i-2}, w_{i-1}, w_i)}{\text{Count}(w_{i-2}, w_{i-1})}
$$

特点

优点

简单直观，易于实现
只需统计有限长度的上下文
在小规模任务和数据量足够时效果较好

缺点

维度灾难：
- $n$ 增大时，参数数量指数级增长随着n增大，泛化能力的优势会减弱。
- 在$n$过小时，n-gram 难以承载足够的语言信息，不足以反应语料库的特性。
稀疏性问题：很多n-gram组合在语料中未出现，概率为0(“零概率” 现象→通过平滑（Smoothing） 技术进行改善)
只能捕捉有限长度的上下文，无法建模长距离依赖
需要大量存储和计算全局统计信息

n-gram vs 词向量

n-gram模型是传统的基于计数的语言建模方法，依赖于统计共现频率。
词向量（如Word2Vec）则通过低维稠密向量对词语进行建模，能够捕捉更丰富的上下文和语义信息。
现代NLP方法常用词向量替代n-gram，提升泛化能力和表达能力。
n-gram模型为理解语言概率建模提供了基础，但其局限性促使我们发展出基于神经网络和词向量的更强大模型。

示例

通过一个 bigrams 语言模型的例子来展示 n-grams 语言模型对文本出现概率进行计算的具体方式。假设语料库中包含 5 个句子:脖子长是长颈鹿最醒目的特征之一。脖子长使得长颈鹿看起来非常优雅，并为其在获取食物上带来便利。有了长脖子的加持，长颈鹿可以观察到动物园里那些隐蔽的角落里发生的事情。长颈鹿脖子和人类脖子一样，只有七节颈椎，也容易患颈椎病。如同长颈鹿脖子由短变长的进化历程一样，语言模型也在不断进化。

基于此语料库，应用 bigrams 对文本”长颈鹿脖子长”（其由 {长颈鹿, 脖子, 长} 三个词构成）出现的概率进行计算，如下式所示：

$$
P_{\text{bigrams}}(\text{长颈鹿, 脖子, 长}) = \frac{C(\text{长颈鹿, 脖子})}{C(\text{长颈鹿})} \cdot \frac{C(\text{脖子, 长})}{C(\text{脖子})}。
$$

在此语料库中，$C(\text{长颈鹿}) = 5, C(\text{脖子}) = 6, C(\text{长颈鹿, 脖子}) = 2, C(\text{脖子, 长}) = 2$，故有：

$$
P_{\text{bigrams}}(\text{长颈鹿, 脖子, 长}) = \frac{2}{5} \cdot \frac{2}{6} = \frac{2}{15}。
$$

在此例中，我们可以发现虽然”长颈鹿脖子长”并没有直接出现在语料库中，但是 bigrams 语言模型仍可以预测出”长颈鹿脖子长”出现的概率有 $\frac{2}{15}$。由此可见，n-grams 具备对未知文本的泛化能力。这也是其相较于传统基于规则的方法的优势。

smoothing

为了解决零概率问题，可以采用平滑技术。平滑技术的基本思想是通过调整模型的概率估计，使得所有n-gram的概率之和为1，同时确保那些在训练数据中未出现过的n-gram也有一个非零的概率估计。以下是几种常见的平滑技术：

加一平滑（Add-One Smoothing/Laplace Smoothing）：
- 对于每个n-gram，其计数加1，然后根据这些调整后的计数来计算概率。
- 公式：$P(w) = \frac{C(w) + 1}{N + V}$
- 其中，C(w)是n-gram w在训练数据中的计数，N是训练数据中的总n-gram数，V是词汇表的大小。
Good-Turing平滑：
- 根据n-gram在训练数据中的出现次数来调整其概率估计，出现次数越多的n-gram，其概率调整的幅度越小。
- 公式： $P(w) = \frac{C(w) + \frac{f(w)}{N}}{N + 1}$
- 其中，f(w)是n-gram w在训练数据中出现的次数。
Kneser-Ney平滑：
- 一种更复杂的平滑方法，它考虑了n-gram的上下文信息，通过估计n-gram的生成概率来计算其概率。
- 公式：$P(w) = \gamma_m \cdot P_{m-1}(w)$, 其中，$\gamma_m$是折扣因子，$P_{m-1}(w)$是$w$作为$(m-1)$-gram出现的概率。折扣因子$\gamma_m$的计算通常依赖于$w$作为$m$-gram出现的次数。
- 这种方法通常比简单的加一平滑或Good-Turing平滑更有效，但计算也更复杂。

通过应用这些平滑技术，n-grams模型可以更好地处理未见过的n-gram，从而提高模型的泛化能力。

【处理零概率的三种平滑方式可迁移的，+1&\N&迭代】

词向量

基本概念

词向量(word vectors)也称为词嵌入(word embeddings)或词表示(word representations),是一种稠密的分布式表示(distributed representation)。

核心思想:”You shall know a word by the company it keeps”

具体实现：通过特定的词嵌入算法(如Word2Vec,GloVe,fasttext等)，训练一个通用的嵌入矩阵即为embedding层。

基于词共现矩阵与SVD分解

概述

简单的one-hot向量无法给出单词间的相似性，我们需要将维度减少至一个低维度的子空间，来获得稠密的词向量，获得词之间的关系。

首先，遍历一个很大的数据集和统计词的共现计数矩阵$X$
然后，对矩阵$X$进行SVD分解得到$X=USV^T$
最后，使用$U$的行来作为字典中所有词的词向量

共现矩阵构建

基于文档(document)——词-文档矩阵
- 最初的解决方法：假设同一篇文章中出现的单词更可能相互关联(猜想相关连的单词在同一个文档中会经常出现)
- 据此建立一个Word-Document矩阵$X$
- 遍历数亿的文档,当词$i$出现在文档$j$，对$X_{ij}$加一
- 矩阵大小为$V \times M$,其中$V$为词汇量,$M$为文章数
- 它的规模是和文档数量M成正比关系,太大了
基于滑窗(window)
- 优化：全文档统计是一件非常耗时耗力的事情→调整为对一个文本窗内的数据进行统计，计算每个单词在特定大小的窗口中出现的次数，得到共现矩阵$X$
- 在每个单词周围使用固定大小的滑窗
- 包含语法(POS)和语义信息
  eg:

SVD降维

共现矩阵的问题

直接使用共现矩阵存在以下问题:

矩阵维度随词汇量增加而增大
需要大量存储空间
矩阵稀疏性导致分类效果不佳

解决方法：SVD降维

我们对共现矩阵 $X$ 使用SVD，观察奇异值（矩阵 $S$ 上对角线元素），根据方差百分比截断，保留前 $k$ 个元素：

$$
\frac{\sum_{i=1}^k \sigma_i}{\sum_{i=1}^{|V|} \sigma_i}
$$

然后取子矩阵 $U_{1:|V|,1:k}$ 作为词嵌入矩阵。这就给出了词汇表中每个词的 $k$ 维表示。

对矩阵 $X$ 使用SVD：

$$
X = U S V^T
$$

其中 $U$、$V$ 为正交矩阵，$S$ 为对角矩阵（奇异值）。

通过选择前 $k$ 个奇异向量来降维：

$$
X \approx U_{1:|V|,1:k} S_{1:k,1:k} V_{1:k,1:|V|}
$$

即只保留前 $k$ 个主成分，得到低维稠密词向量。

新的问题：

前面提到的方法给我们提供了足够的词向量来编码语义和句法（part of speech）信息，但也带来了一些问题：

矩阵的维度会经常发生改变（经常增加新的单词和语料库的大小会改变）
矩阵会非常稀疏，因为很多词不会共现
矩阵维度一般会非常高，通常 $10^6 \times 10^6$
需要在 $X$ 上加入一些技巧处理来解决词频的极剧不平衡

基于SVD的方法的计算复杂度很高（$m \times n$ 矩阵的计算成本是 $O(mn^2)$），并且很难合并新单词或文档。

对上述问题的改进方法：

忽略功能词，例如”the”，”he”，”has”等等
使用 ramp window，即根据文档中单词之间的距离对共现计数进行加权
使用皮尔逊相关系数并将负计数设置为 $0$，而不是只使用原始计数

Word2Vec

总览

基本思想

Word2Vec是一个学习词向量表征的框架:

它是一个迭代模型，能够根据文本进行迭代学习。最终能够对给定上下文的单词的概率(“You shall know a word by the company it keeps” )，对词向量进行编码呈现，而不是计算和存储一些大型数据集(可能是数十亿个句子)的全局信息。
设计一个模型，该模型的参数就是词向量。然后根据一个目标函数训练模型，在每次模型的迭代计算误差，基于优化算法调整模型参数（词向量），减小损失函数，从而最终学习到词向量。(神经网络中对应的思路叫”反向传播”)

核心特征：

基于海量文本语料库构建
词汇表中的每个单词都由一个向量表示（学习完成后会固定）
使用中心词预测上下文词(或反之)：对应语料库文本中的每个位置t，有一个中心词c和一些上下文(外部)单词o。使用c和o的词向量来计算概率$P(o|c)$(或反之)
不断调整词向量减小损失函数，以最大化预测概率

eg: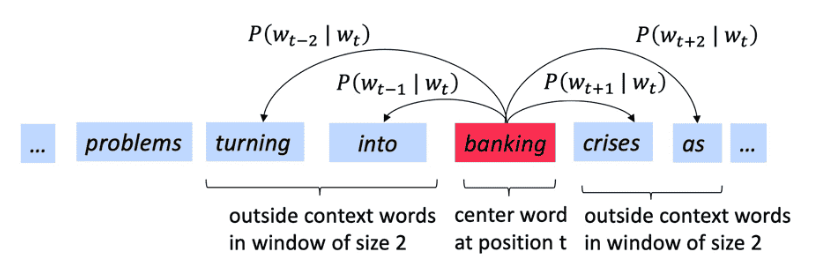

目标函数

对于每个位置$t$,在大小为$m$的固定窗口内预测上下文单词,给定中心词$w_t$,
似然函数:

$$L(\theta) = \prod_{t=1}^T \prod_{-m \leq j \leq m, j \neq 0} P(w_{t+j}|w_t;\theta)$$

目标函数为(平均)负对数似然:

$$J(\theta) = -\frac{1}{T}\sum_{t=1}^T \sum_{-m \leq j \leq m, j \neq 0} \log P(w_{t+j}|w_t;\theta)$$

注意：

上述目标函数中的log形式是方便将连乘转化为求和，在连乘之前使用log转化为求和非常有效，特别是做优化时。
负号是希望将极大化似然率转化为极小化损失函数的等价问题。最小化目标函数↔最大化似然函数（预测概率/精度），两者等价。

概率估计

对于每个词 $w$，Word2Vec 都会用两个向量：

当 $w$ 是中心词时，记作词向量 $v_w$
当 $w$ 是上下文词时，记作词向量 $u_w$

对于一个中心词 $c$ 和一个上下文词 $o$，我们有如下概率计算方式：
$$
P(o|c) = \frac{\exp(u_o^T v_c)}{\sum_{w \in V} \exp(u_w^T v_c)}
$$

其中：

$v_c$：中心词 $c$ 的词向量
$u_o$：上下文词 $o$ 的词向量
$V$：词汇表

Word2Vec的目标是最大化真实上下文词出现的概率，等价于最小化负对数似然（cross-entropy）：
$$
J(\theta) = -\frac{1}{T} \sum_{t=1}^T \sum_{-m \leq j \leq m, j \neq 0} \log P(w_{t+j} | w_t; \theta)
$$

其中：

$T$：语料库中单词总数
$m$：窗口大小
$w_t$：第$t$个中心词
$w_{t+j}$：窗口内的上下文词

补充说明：

公式中，向量 $u_o$ 和 $v_c$ 进行点积。
向量之间越相似，点积结果越大，从而归一化后得到的概率值也越大。
该目标函数的本质是让有相似上下文的单词，具有相似的向量。
点积是计算相似性的一种简单方法，在注意力机制中常用作Score。

模型变体

Word2Vec有SG/CBOW两个主要变体。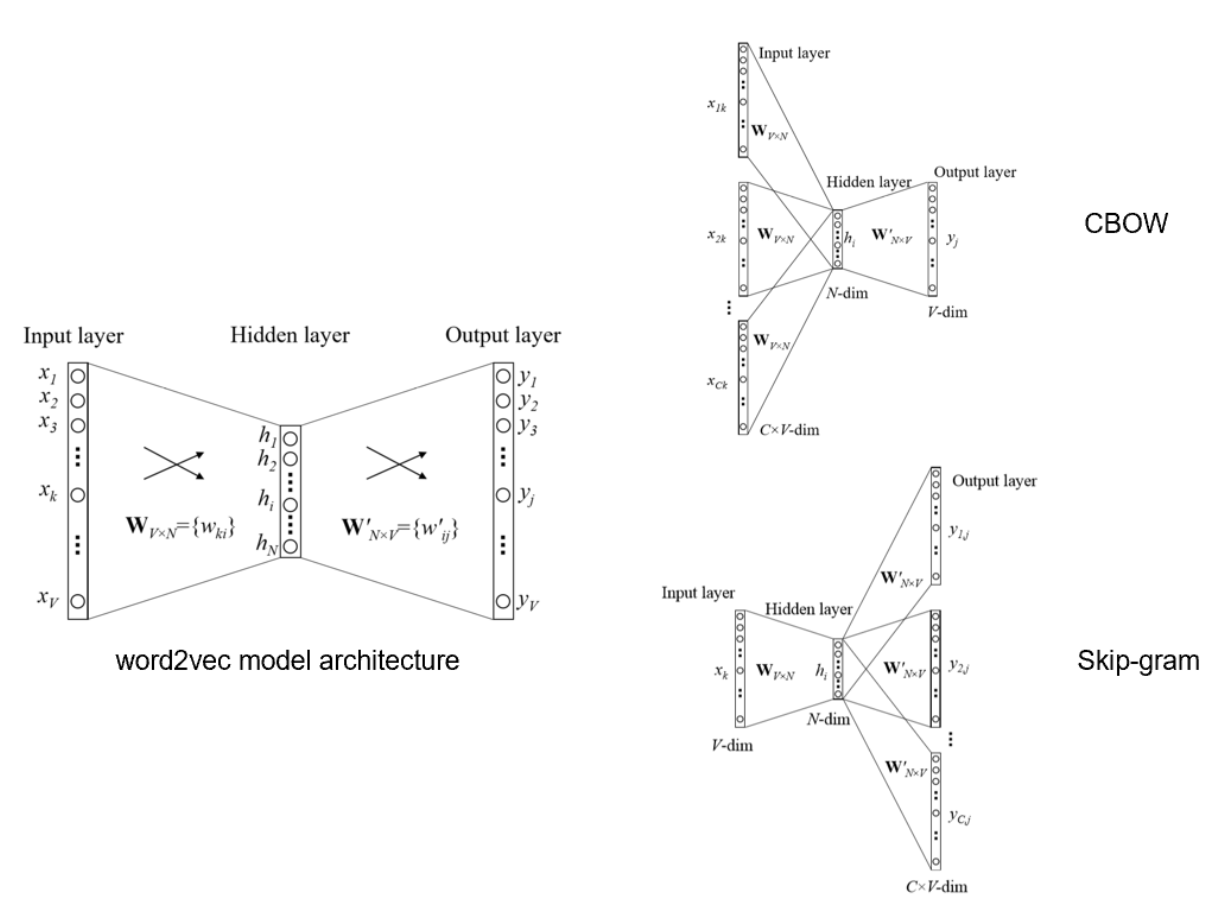

Skip-grams (SG)

基本概念

基本思想
- 输入中心词并预测上下文中的单词
- 模型输入、输出是one-hot形式的词向量表示。
公式推导
- 对于中心词 $w_t$ 和上下文词 $w_{t+j}$，我们定义：
  - $v_{w_t}$ 为中心词的词向量
  - $u_{w_{t+j}}$ 为上下文词的词向量
- 使用 softmax 函数计算条件概率，得到目标函数：
  $$P(w_{t+j}|w_t) = \frac{\exp(u_{w_{t+j}}^T v_{w_t})}{\sum_{w=1}^V \exp(u_w^T v_{w_t})}$$
- 其中分母是对词汇表中所有词的归一化项
- 目标是最小化负对数似然：
  $$J = -\frac{1}{T}\sum_{t=1}^T \sum_{-m \leq j \leq m, j \neq 0} \log P(w_{t+j}|w_t)$$
训练过程
- 对每个中心词，计算其与所有上下文词的相似度
- 使用梯度下降更新词向量
- 通过最大化真实上下文词的概率，同时最小化其他词的概率

详细推导

符号说明

$x$: 输入的one-hot向量，表示上下文词
$y$: 输出的one-hot向量，表示中心词
$v$: 输入词嵌入向量（当词作为输入时使用）
$u$: 输出词嵌入向量（当词作为输出时使用）

参数定义

设词汇表大小为$|V|$，嵌入维度为$n$。词汇表$V$中的单词$w_i$。
定义两个参数矩阵：
- $V \in \mathbb{R}^{n \times |V|}$：输入词嵌入矩阵，第$i$列$v_i$为词$w_i$的输入向量。
- $U \in \mathbb{R}^{|V| \times n}$：输出词嵌入矩阵，第$j$行$u_j$为词$w_j$的输出向量。

输入输出向量说明

输入：上下文窗口内$2m$个词的one-hot向量$x^{(c-m)},\ldots,x^{(c-1)},x^{(c+1)},\ldots,x^{(c+m)} \in \mathbb{R}^{|V|}$。
- 每个$x^{(i)}$是一个$|V|$维的one-hot向量，只有对应词的位置为1，其他位置为0
嵌入查找：$v_{c-m} = V x^{(c-m)},\ v^{(c-m+1)} = V x^{(c-m+1)} \ ,\ldots, \ v_{c+m} = V x^{(c+m)}$。
- 这一步将one-hot向量转换为词嵌入向量(每个单词被映射为一个低维的连续向量，有各种可能的数值，通常维度较小)
- 例如：如果$x^{(c-m)}$是”cat”的one-hot向量[0,0,1,0…0]，那么$v_{c-m}$就是”cat”的词嵌入向量[0.2,-0.5,…]
上下文向量平均：
$$
\bar{v} = \frac{1}{2m} (v_{c-m} + v_{c-m+1} + \ldots + v_{c+m})
$$
- 将窗口内所有上下文词的词嵌入向量取平均，得到上下文表示

计算得分与概率

相似的词对的向量的点积值大，这会令相似的词更为靠近，从而获得更高的分数。

得分向量：
$$
z = U \bar{v} \in \mathbb{R}^{|V|}
$$
- $z$的每个元素$z_i$表示词汇表中第$i$个词与当前上下文的相似度
- 点积越大，表示该词与当前上下文越相关
softmax概率：
$$
\hat{y} = \text{softmax}(z) = \frac{\exp(z)}{\sum_{k=1}^{|V|} \exp(z_k)} = \frac{\exp(u_j^T v_c)}{\sum_{k=1}^{|V|} \exp(u_k^T v_c)}
$$
- 将得分转换为概率分布
- 每个元素$\hat{y}_i$表示预测第$i$个词作为中心词的概率

损失函数（交叉熵）

真实标签$y$为one-hot向量，中心词索引为$c$。
损失函数：
$$
H(\hat{y}, y) = - \sum_{j=1}^{|V|} y_j \log \hat{y}_j = -\log \hat{y}_c
$$
- 由于$y$是one-hot向量，只有$y_c=1$，其他位置为0
- 所以求和后只剩下$-\log \hat{y}_c$项
展开得：
$$
H(\hat{y}, y) = -u_c^T \bar{v} + \log \sum_{k=1}^{|V|} \exp(u_k^T \bar{v})
$$
- 第一项$-u_c^T \bar{v}$：真实中心词的得分
- 第二项$\log \sum_{k=1}^{|V|} \exp(u_k^T \bar{v})$：所有可能词的得分的对数归一化项

梯度更新

对$U$和$V$分别用SGD更新：
$$
U \leftarrow U - \alpha \nabla_U J, \quad V \leftarrow V - \alpha \nabla_V J
$$
- $\alpha$是学习率
- $\nabla_U J$和$\nabla_V J$分别是损失函数对$U$和$V$的梯度
- 通过梯度下降最小化损失函数，使预测概率更接近真实分布

Continuous Bag of Words (CBOW)

基本概念

基本思想
- 输入上下文中的单词并预测中心词
- 模型输入、输出是one-hot形式的词向量表示。
公式推导
- 对于上下文窗口 $w_{t-m},…,w_{t-1},w_{t+1},…,w_{t+m}$ 和中心词 $w_t$：
  - 首先计算上下文词向量的平均值：
    $$\bar{v} = \frac{1}{2m}\sum_{-m \leq j \leq m, j \neq 0} v_{w_{t+j}}$$
  - 使用 softmax 函数计算条件概率，得到目标函数：
    $$P(w_t|w_{t-m},…,w_{t-1},w_{t+1},…,w_{t+m}) = \frac{\exp(u_{w_t}^T \bar{v})}{\sum_{w=1}^V \exp(u_w^T \bar{v})}$$
- 目标是最小化负对数似然：
  $$J = -\frac{1}{T}\sum_{t=1}^T \log P(w_t|w_{t-m},…,w_{t-1},w_{t+1},…,w_{t+m})$$
训练过程
- 对每个上下文窗口，计算上下文词向量的平均值
- 使用梯度下降更新词向量
- 通过最大化真实中心词的概率，同时最小化其他词的概率

详细推导

符号说明

$x$: 输入的one-hot向量，表示上下文词
$y$: 输出的one-hot向量，表示中心词
$v$: 输入词嵌入向量（当词作为输入时使用）
$u$: 输出词嵌入向量（当词作为输出时使用）

参数定义

设词汇表大小为$|V|$，嵌入维度为$n$。词汇表$V$中的单词$w_i$。
定义两个参数矩阵：
- $V \in \mathbb{R}^{n \times |V|}$：输入词嵌入矩阵，第$i$列$v_i$为词$w_i$的输入向量。
- $U \in \mathbb{R}^{|V| \times n}$：输出词嵌入矩阵，第$j$行$u_j$为词$w_j$的输出向量。

输入输出向量说明

输入：中心词one-hot向量$x_c \in \mathbb{R}^{|V|}$。
嵌入查找：$v_c = V x_c$。
输出：每个上下文词的one-hot向量$y_{c+j}$。

计算得分与概率

对每个上下文词$w_{c+j}$，得分：
$$
z = U v_c \in \mathbb{R}^{|V|}
$$
softmax概率：
$$
\hat{y}_j = \text{softmax}(z) = \frac{\exp(z)}{\sum_{k=1}^{|V|} \exp(z_k)} = \frac{\exp(u_j^T v_c)}{\sum_{k=1}^{|V|} \exp(u_k^T v_c)}
$$

损失函数（窗口内所有上下文词）

真实标签$y^{(c+j)}$为one-hot向量。
总损失：
$$
J = - \sum_{j=-m, j\neq 0}^{m} \log P(w_{c+j}|w_c) = - \sum_{j=-m, j\neq 0}^{m} \log \hat{y}_{c+j}
$$
展开得：
$$
J = - \sum_{j=-m, j\neq 0}^{m} \left[ u_{c+j}^T v_c - \log \sum_{k=1}^{|V|} \exp(u_k^T v_c) \right]
$$

梯度更新

对$U$和$V$分别用SGD更新：
$$
U \leftarrow U - \alpha \nabla_U J, \quad V \leftarrow V - \alpha \nabla_V J
$$

SG vs CBOW

词向量模型变体	Skip-gram (SG)	CBOW
训练目标	用中心词预测上下文	用上下文预测中心词
输入	中心词	上下文词（窗口内所有词）
输出	上下文词（窗口内所有词）	中心词
适用场景	小数据集、低频词、罕见词	大数据集、高频词
对罕见词表现	更好	一般
对高频词表现	一般	更好
训练速度	慢（每个样本生成多个训练对）	快（每个样本只生成一个训练对）
上下文利用	每次只用一个上下文词	同时利用全部上下文词
词向量质量	低频词效果好，整体表现略优	高频词效果好，整体表现略逊
计算复杂度	较高	较低

训练方法

Word2Vec的训练目标是通过优化目标函数，学习到能够表达语义和上下文关系的词向量。
由于词表通常非常大，直接用softmax计算概率的代价极高，因此实际训练中常用两种高效的近似方法：负采样（Negative Sampling）和层次化Softmax（Hierarchical Softmax）。

负采样

Negative Sampling

基本思想

不是对整个词表做softmax归一化，而是将多分类问题转化为一系列二分类问题。
对每个正样本（中心词与真实上下文词对），随机采样若干负样本（中心词与语料库中随机词的组合），让模型区分”真实上下文”与”噪声词”。
本质上是用逻辑回归判别”这对词是否真实共现”。

数学推导

设中心词为 $c$，上下文词为 $w$，词向量分别为 $v_c$ 和 $u_w$。
对于正样本 $(c, w)$，希望模型输出概率接近1；对于负样本 $(c, w_k)$，希望输出概率接近0。

正样本概率：
$$
P(D=1|c, w) = \sigma(u_w^T v_c) = \frac{1}{1 + e^{-u_w^T v_c}}
$$
负样本概率：
$$
P(D=0|c, w_k) = 1 - \sigma(u_{w_k}^T v_c) = \sigma(-u_{w_k}^T v_c)
$$

其中 $\sigma(x)$ 是sigmoid函数。

单个训练样本的目标函数：
$$
J = \log \sigma(u_w^T v_c) + \sum_{k=1}^K \mathbb{E}_{w_k \sim P_n(w)} [\log \sigma(-u_{w_k}^T v_c)]
$$
其中 $K$ 是负样本数量，$P_n(w)$ 是负样本的采样分布（通常按词频的3/4次方归一化）。
全局损失函数（对所有训练对求和，取负号做最小化）：
$$
J = - \sum_{(c, w) \in D} \left[ \log \sigma(u_w^T v_c) + \sum_{k=1}^K \log \sigma(-u_{w_k}^T v_c) \right]
$$

采样分布

负样本的采样分布 $P_n(w)$ 通常设为：
$$
P_n(w) = \frac{f(w)^{3/4}}{\sum_{j} f(w_j)^{3/4}}
$$
其中 $f(w)$ 是词 $w$ 的词频。3/4次方可以提升低频词被采样的概率，避免高频词过多。

优点

计算复杂度大幅降低，每次只需计算 $K+1$ 个词的向量点积。
适合大规模语料和词表。

层次化Softmax

Hierarchical Softmax

基本思想

用一棵二叉树表示整个词表，每个叶节点对应一个词。
计算某个词的概率时，只需沿树从根到该词的叶节点的路径，依次做二分类决策，复杂度 $O(\log |V|)$。
每个内部节点有一个向量，表示”走左/右子树”的概率。

数学推导

设词 $w$ 的路径为 $n(w, 1), n(w, 2), …, n(w, L(w))$，$L(w)$ 为路径长度。
$ch(n)$ 表示节点 $n$ 的左子节点。
$[x]$ 表示布尔值，$x$为真时取1，否则取-1。
概率公式：
$$
P(w|c) = \prod_{j=1}^{L(w)-1} \sigma\left( [n(w, j+1) = ch(n(w, j))] \cdot v_{n(w, j)}^T v_c \right)
$$
- $v_{n(w, j)}$：路径上第 $j$ 个内部节点的向量
- $v_c$：中心词的向量
解释：
- 每经过一个内部节点，判断是走左还是右，sigmoid输出概率。
- 整个词的概率是路径上所有决策概率的连乘。

损失函数

训练目标是最小化负对数似然：
$$
J = -\log P(w|c)
$$

优点

计算复杂度 $O(\log |V|)$，适合超大词表。
对低频词的概率估计更平滑。

总结对比

方法	计算复杂度	适用场景	主要思想
负采样	$O(K)$	词表极大	多分类转为多次二分类
层次化Softmax	$O(log\|V\|)$	词表极大	二叉树路径概率连乘
普通Softmax	$O(\|V\|)$	词表较小	全词表归一化

参考公式小结：

sigmoid函数：
$$
\sigma(x) = \frac{1}{1 + e^{-x}}
$$
负采样目标函数：
$$
J = \log \sigma(u_w^T v_c) + \sum_{k=1}^K \log \sigma(-u_{w_k}^T v_c)
$$
层次化Softmax概率：
$$
P(w|c) = \prod_{j=1}^{L(w)-1} \sigma\left( [n(w, j+1) = ch(n(w, j))] \cdot v_{n(w, j)}^T v_c \right)
$$

GloVe

核心思想

GloVe（Global Vectors for Word Representation）是一种基于全局统计信息的词向量训练方法。
其核心观点是：词与词之间的语义关系可以通过共现概率的比值来编码，而不仅仅是概率本身的大小。

不同词对与上下文词的共现概率的比值，能够揭示词语的语义成分（meaning component）。
例如，区分”ice”（冰）和”steam”（蒸汽）时，
- 与”solid”（固体）共现的概率 $P(\text{solid}|\text{ice})$ 远大于 $P(\text{solid}|\text{steam})$，
- 与”gas”（气体）共现的概率 $P(\text{gas}|\text{steam})$ 远大于 $P(\text{gas}|\text{ice})$，
- 与”water”共现的概率二者接近，
- 与”fashion”共现的概率都很小且相近。

这些概率的比值，而非单独的概率值，才真正反映了词语之间的语义差异。

数学推导

log-bilinear模型：点积等于概率对数，向量差异等于概率比值的对数。
GloVe目标：用词向量点积加偏置去拟合共现次数的对数。
损失函数：用平方损失拟合目标关系，并用权重函数降权高频词对。
几何意义：词向量空间的结构（如向量差异）能够表达词语之间的概率比值和语义关系。

log-bilinear模型与向量差异

GloVe的本质思想可以追溯到log-bilinear模型：

对于词$i$和$j$，希望有：
$$
w_i \cdot w_j = \log P(i|j)
$$
对于向量差异：
$$
w_x \cdot (w_a - w_b) = \log \frac{P(x|a)}{P(x|b)}
$$
向量差异 $w_a - w_b$ 在 $w_x$ 方向上的投影，反映了 $x$ 与 $a$、$b$ 的共现概率比值的对数, 进而编码语义成分。
GloVe实际上是将 log-bilinear 的思想应用到所有词对 $(i, j)$，用词向量的点积（加偏置）去拟合共现次数的对数。
这样，词向量空间的结构就能反映概率比值的对数，也就是语义关系。

共现概率

设词汇表为 $V$，$X_{ij}$ 表示词 $j$ 作为词 $i$ 上下文出现的次数。
词 $i$ 的所有上下文出现总次数为 $X_i = \sum_k X_{ik}$。
词 $j$ 在词 $i$ 上下文中出现的条件概率为：
$$
P_{ij} = P(j|i) = \frac{X_{ij}}{X_i}
$$

比值编码语义

对于目标词 $i$，上下文词 $j$ 和 $k$，我们关注比值：
$$
\frac{P_{ik}}{P_{jk}}
$$
这个比值可以反映 $k$ 与 $i$、$j$ 的语义相关性差异。
例如，$k$ 为”solid”，$i$ 为”ice”，$j$ 为”steam”时，这个比值远大于1，说明”solid”更常与”ice”共现。

模型目标

GloVe希望通过词向量的差值来刻画这种概率比值关系。
设 $w_i$、$\tilde{w}_j$ 分别为词 $i$ 和上下文词 $j$ 的词向量，$b_i$、$\tilde{b}_j$ 为偏置项。
设计如下关系：
$$
F(w_i, \tilde{w}_j, b_i, \tilde{b}_j) = w_i^T \tilde{w}_j + b_i + \tilde{b}_j \approx \log X_{ij}
$$
即词向量的内积加偏置，拟合词对的共现次数的对数。
进一步，GloVe的损失函数为：
$$
J = \sum_{i,j=1}^V f(X_{ij}) \left( w_i^T \tilde{w}_j + b_i + \tilde{b}_j - \log X_{ij} \right)^2
$$
其中 $f(X_{ij})$ 是权重函数，用于降低高频词对的影响，常用形式为：
$$
f(x) = \begin{cases}
(x/x_{max})^\alpha & \text{if } x < x_{max} \\
1 & \text{otherwise}
\end{cases}
$$
典型参数：$x_{max}=100$, $\alpha=0.75$。

总结

GloVe通过对共现概率的比值进行建模，利用全局统计信息，学习到能够表达丰富语义关系的词向量。
其损失函数本质上是让词向量的内积加偏置，去拟合词对的共现次数的对数。
这种方法不仅能捕捉到类似Word2Vec的语义关系，还能更好地反映全局统计特性。

GloVe与Word2Vec的对比:

方法	统计信息	优点	训练方式
Word2Vec	局部上下文窗口	训练快，适合大语料	预测型
GloVe	全局共现矩阵	语义关系更丰富	计数+回归拟合

公式小结：

共现概率：
$$
P_{ij} = \frac{X_{ij}}{X_i}
$$
目标关系：
$$
w_i^T \tilde{w}_j + b_i + \tilde{b}_j \approx \log X_{ij}
$$
损失函数：
$$
J = \sum_{i,j=1}^V f(X_{ij}) \left( w_i^T \tilde{w}_j + b_i + \tilde{b}_j - \log X_{ij} \right)^2
$$

词向量训练与评估

训练过程

数据预处理

文本清洗：去除特殊字符、标点符号等
分词：将文本分割成单词序列
构建词汇表：统计词频，去除低频词
构建训练样本：根据窗口大小生成中心词-上下文词对

模型训练

初始化词向量：随机初始化或预训练
批量训练：使用mini-batch SGD优化
学习率调整：通常使用学习率衰减策略
早停：根据验证集性能决定是否停止训练

训练技巧

负采样：减少计算复杂度
层次化Softmax：加速训练
词向量平均：提高稳定性
梯度裁剪：防止梯度爆炸

评估方法

内在评估

Intrinsic Evaluation

词义类比任务
- 计算词向量之间的余弦相似度
- 评估语义和语法关系
- 示例：king - man + woman ≈ queen
词义相似度任务
- 使用WordSim-353等数据集
- 计算预测相似度与人工标注的相关性
聚类评估
- 对词向量进行聚类
- 评估聚类结果的语义一致性

外在评估

Extrinsic Evaluation

命名实体识别（NER）
词性标注（POS Tagging）
情感分析（Sentiment Analysis）
文本分类（Text Classification）

评估指标

准确率（Accuracy）
精确率（Precision）和召回率（Recall）
F1分数
平均倒数排名（Mean Reciprocal Rank, MRR）
平均精度均值（Mean Average Precision, MAP）

超参数影响

词向量维度

通常选择100-300维
维度与性能的关系：
$$
\text{Performance} = \alpha \log(d) + \beta
$$
其中$d$为维度，$\alpha$和$\beta$为常数

上下文窗口大小

影响捕获的上下文信息范围
通常选择5-10
窗口大小与性能的关系：
$$
\text{Context Score} = \sum_{i=-w}^{w} \frac{1}{|i|+1} \cdot \text{Similarity}(w_i, w_0)
$$
其中$w$为窗口大小

训练参数

学习率：通常从0.025开始，逐渐衰减
批量大小：通常选择32-128
训练轮数：根据验证集性能决定
负样本数：通常选择5-20

词义歧义处理

多义词表示

线性叠加模型：
$$
v_{word} = \sum_{i=1}^{k} \alpha_i v_{sense_i}
$$
其中$\alpha_i$为各词义的权重

上下文感知

动态词向量：
$$
v_{word}^{context} = f(v_{word}, c)
$$
其中$c$为上下文信息

多义词原型方法

基于论文《Improving Word Representations Via Global Context And Multiple Word Prototypes》的方法：

上下文收集
- 对每个词收集固定大小的上下文窗口（如前5后5）
- 构建上下文表示：
  $$
  c_w = \sum_{i \in \text{window}} \text{IDF}(i) \cdot v_i
  $$
  其中$\text{IDF}(i)$为词$i$的逆文档频率
聚类分析
- 使用spherical k-means对上下文表示进行聚类
- 目标函数：
  $$
  \min_{C_1,…,C_k} \sum_{i=1}^k \sum_{c \in C_i} |c - \mu_i|^2
  $$
  其中$C_i$为第$i$个簇，$\mu_i$为簇中心
词向量训练
- 根据聚类结果重新标注词的出现
- 对每个簇分别训练词向量
- 最终词向量为各簇向量的加权和：
  $$
  v_{word} = \sum_{i=1}^k p(i|word) \cdot v_{word}^i
  $$
  其中$p(i|word)$为词属于第$i$个簇的概率
实现细节
- 上下文窗口大小：通常5-10
- 聚类数量：根据词的多义性程度动态调整
- 权重计算：使用TF-IDF或注意力机制
- 训练策略：分阶段训练，先聚类后微调

评估方法

多义词评估数据集
- SemCor：包含词义标注的语料库
- WordNet：同义词集评估
- 上下文相似度评估
上下文相关度评估
- 计算不同上下文下的词向量相似度
- 评估词义区分能力
词义消歧准确率
- 在标准数据集上的消歧性能
- 与基线方法的对比

应用场景

机器翻译
- 根据上下文选择正确的词义
- 提高翻译准确性
信息检索
- 考虑词的多义性
- 提高检索相关性
文本分类
- 利用多义词的不同含义
- 提升分类性能
问答系统
- 理解问题的具体语境
- 提供更准确的答案

秋月春风

明月守灯寻长梦，梦长寻灯守月明

明月守灯寻长梦，梦长寻灯守月明

秋月春风

NLP介绍

自然语言

词汇含义

计算机中表达词义

离散式表示

WordNet

one-hot

词袋模型

基本思想

具体示例

优缺点

TF-IDF

基本概念

计算示例

特点

n-gram

分布式表示

核心：基于上下文

词向量

NLP任务

n-gram

基本思想

Unigram

Bigram

Trigram

n-gram

概率估计

特点

优点

缺点

n-gram vs 词向量

示例

smoothing

词向量

基本概念

基于词共现矩阵与SVD分解

概述

共现矩阵构建

SVD降维

共现矩阵的问题

解决方法：SVD降维

Word2Vec

总览

基本思想

目标函数

概率估计

模型变体

Skip-grams (SG)

基本概念

详细推导

符号说明

参数定义

输入输出向量说明

计算得分与概率

损失函数（交叉熵）

梯度更新

Continuous Bag of Words (CBOW)

基本概念

详细推导

符号说明

参数定义

输入输出向量说明

计算得分与概率

损失函数（窗口内所有上下文词）

梯度更新

SG vs CBOW

训练方法

负采样

基本思想

数学推导

层次化Softmax

基本思想

数学推导

总结对比

GloVe

核心思想