参考：
神经网络基础
大部分数据是线性不可分的所以需要非线性分类器，神经网络是一类具有非线性决策分界的分类器。
神经网络是受生物学启发的分类器，常被称为”人工神经网络”，以区别于有机类。
单个神经元
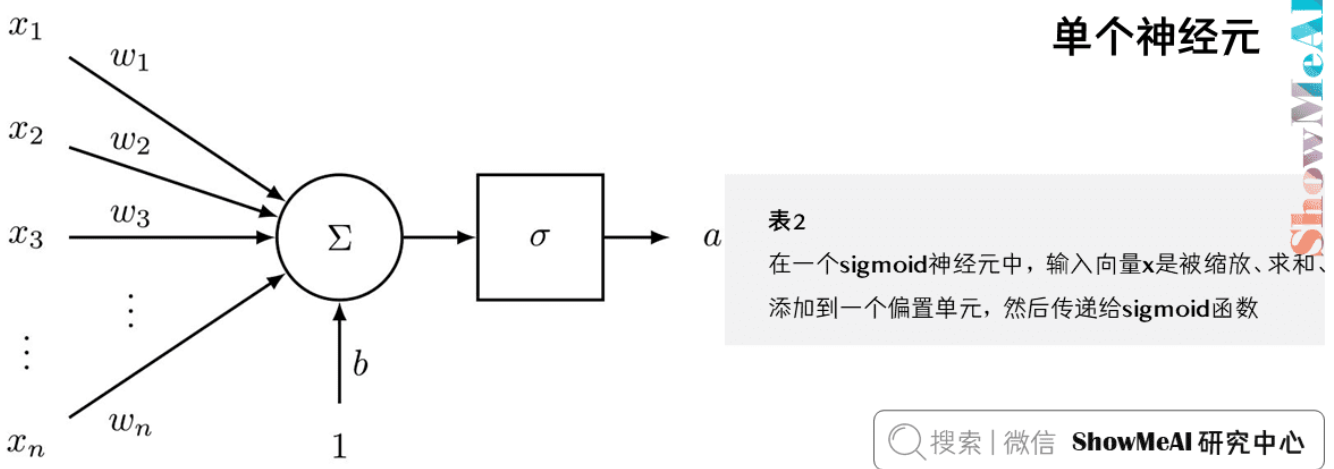
神经网络的基本组成单元是神经元，它模拟了人脑神经元的工作方式。每个神经元接收多个输入信号，经过处理后产生一个输出信号。
- 神经元是一个通用的计算单元，接受n个输入并产生一个输出
- 常见的神经元选择是二元逻辑回归单元，它能够将输入映射到[0,1]区间
- 神经元与n维权重向量w和偏置标量b相关联，这些参数决定了神经元的行为
- 输出计算公式：$a = \frac{1}{1 + e^{-(w^Tx + b)}}$，这个公式称为sigmoid函数，记作 $\sigma$
- 为了简化计算，可以将权重和偏置合并：$a = \frac{1}{1 + e^{-[w^T, b] \cdot [x, 1]}}$
单层神经网络
单层神经网络是多个神经元的组合，它们并行工作，共同处理输入数据。这种结构能够学习更复杂的特征表示。
- 将单个神经元扩展到多个神经元，形成一层网络
- 定义不同神经元的权重、偏置和激活输出：
- 权重矩阵：$W \in \mathbb{R}^{n \times m}$，表示输入到输出的映射关系
- 偏置向量：$b \in \mathbb{R}^m$，用于调整每个神经元的激活阈值
- 激活输出：$a = \sigma(Wx + b)$，其中σ是激活函数
- 使用矩阵形式简化表达：
- $z = Wx + b$，这是线性变换部分
- $a = \sigma(z)$，这是非线性激活部分
- 激活函数用于捕捉非线性特征组合，使网络能够学习复杂的模式
- 维度分析：如果使用d维词向量，窗口大小为n，则输入维度为$n \times d$
前向与反向计算
神经网络的计算分为前向传播和反向传播两个阶段。前向传播用于计算输出，反向传播用于更新参数。
- 前向计算：输入向量经过一层单元变换得到激活输出
- 输入层：$x \in \mathbb{R}^{n \times d}$，原始输入数据
- 隐藏层：$h = \sigma(W_1x + b_1)$，第一层变换
- 输出层：$s = W_2h + b_2$，最终输出
- 反向计算：通过链式法则计算梯度，用于参数更新
- 输出层梯度：$\frac{\partial L}{\partial W_2} = \frac{\partial L}{\partial s} \cdot h^T$，表示输出层参数对损失的影响
- 隐藏层梯度：$\frac{\partial L}{\partial W_1} = \frac{\partial L}{\partial h} \cdot x^T$，表示隐藏层参数对损失的影响
- 维度分析：考虑词向量维度、窗口大小等，确保矩阵运算维度匹配
合页损失
合页损失（Hinge Loss）是一种常用的损失函数，特别适用于分类问题。
它通过最大化正负样本之间的间隔来提高模型的泛化能力。
- 常用的误差度量方法：maximum margin objective 最大间隔目标函数——确保分类边界有足够的间隔
- 保证”真”标签得分高于”假”标签，提高分类准确性
- 引入安全间隔Δ，增加模型的鲁棒性
- 优化目标函数：$J = \max(0, s_c - s + \Delta)$，其中$s_c$是正确类别的得分
- 完整损失函数：$J = \frac{1}{N}\sum_{i=1}^N \max(0, s_c^{(i)} - s^{(i)} + \Delta)$，考虑所有样本
- 梯度计算：
- 当$s_c - s + \Delta > 0$时：$\frac{\partial J}{\partial s} = -1$，需要降低错误类别的得分
- 当$s_c - s + \Delta \leq 0$时：$\frac{\partial J}{\partial s} = 0$，已经达到目标间隔
反向传播
反向传播是神经网络训练的核心算法，它通过链式法则计算每个参数对损失的贡献，从而指导参数更新。
单样本形态
- 利用微分链式法则计算梯度，实现端到端的梯度传播
- 误差共享/分配机制，确保每个参数得到合适的更新
- 偏置更新规则：偏置的梯度等于输出梯度
详细推导
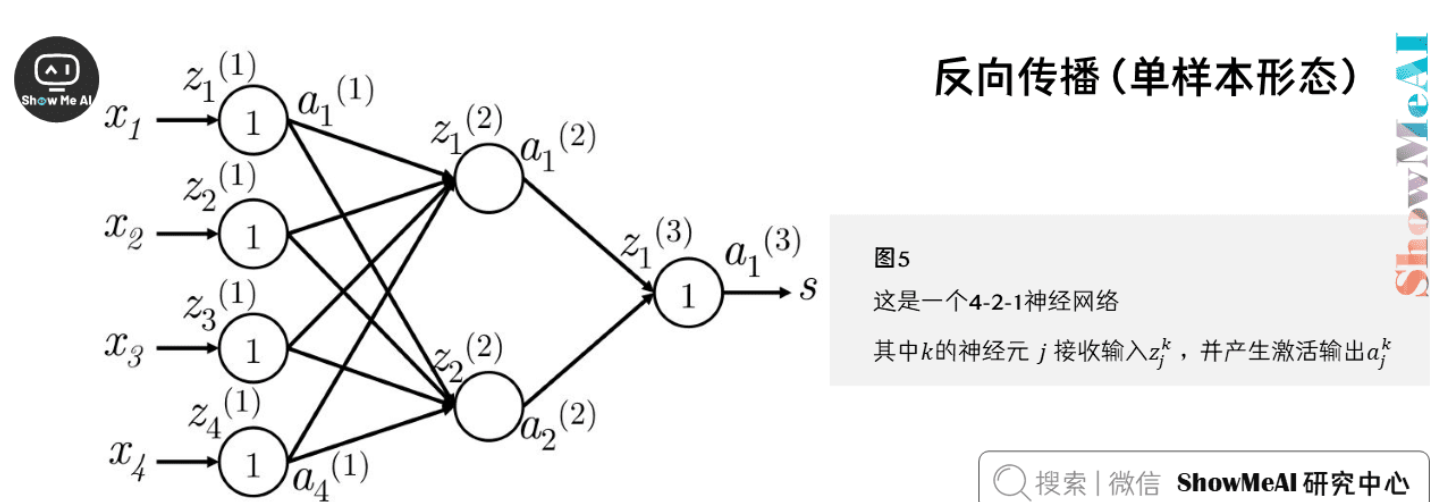
以单个隐藏层和单个输出单元的神经网络为例。建立一些符号定义：
- $x_i$：神经网络的输入
- $s$：神经网络的输出
- 每层（包括输入和输出层）的神经元都接收一个输入并生成一个输出。第$k$层的第$j$个神经元接收标量输入$z_j^{(k)}$，并生成一个标准激活输出$a_j^{(k)}$
- 反向传播误差定义为$\delta_j^{(k)}$
- 第1层是输入层，而不是第1个隐藏层。对输入层而言，$x_j = z_j^{(1)} = a_j^{(1)}$
- $W^{(k)}$是将第$k$层的输出映射到第$k+1$层输入的转移矩阵。例如$W^{(1)}=W, W^{(2)}=U$
假设损失函数$J=(1+s_c-s)$为正值，想更新参数$W_{14}^{(1)}$，它只参与$z_1^{(2)}$和$a_1^{(2)}$的计算。
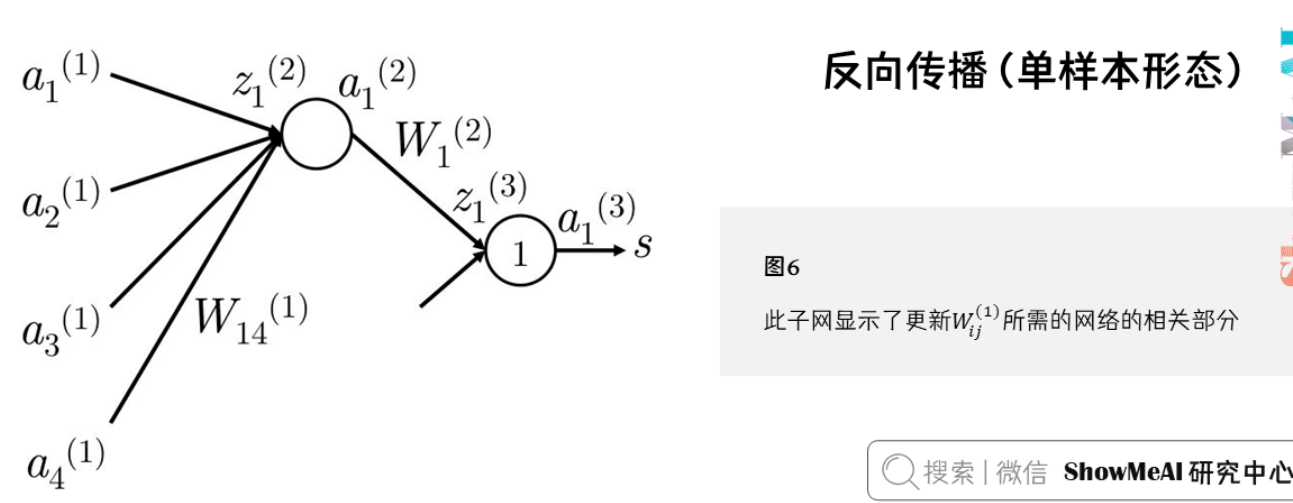
反向传播的梯度只受它们所贡献的值的影响。
$a_1^{(2)}$在前向计算中和$W_1^{(2)}$相乘计算得分。
最大间隔损失下：
$$
\frac{\partial J}{\partial s} = \frac{\partial J}{\partial s_c} = -1
$$
为了简化只分析$\frac{\partial s}{\partial W_{ij}^{(1)}}$，所以：
$$
\frac{\partial s}{\partial W_{ij}^{(1)}} = \sum_i W_i^{(2)} f’(z_i^{(2)}) a_j^{(1)}
$$
详细链式法则推导如下：
$$
\frac{\partial s}{\partial W_{ij}^{(1)}} = \frac{\partial s}{\partial a_i^{(2)}} \frac{\partial a_i^{(2)}}{\partial z_i^{(2)}} \frac{\partial z_i^{(2)}}{\partial W_{ij}^{(1)}}
$$
$$
= W_i^{(2)} f’(z_i^{(2)}) a_j^{(1)}
$$
其中$a_j^{(1)}$指输入层的输入。最终梯度可简化为$\delta_i^{(2)} a_j^{(1)}$，其中$\delta_i^{(2)}$本质上是第2层第$i$个神经元反向传播的误差。
偏置更新
偏置项的更新和权值在数学形式上是等价的，只是在计算下一层神经元输入时相乘的值是常量1。
一般步骤
- 有$\delta_i^{(k)}$向后传播的误差$\delta_j^{(k-1)}$
- $\delta_i^{(k)}$与路径上的权值$w_{ij}^{(k-1)}$相乘，误差反向传播到$a_j^{(k-1)}$
- $a_j^{(k-1)}$接收的误差是$\delta_i^{(k)} w_{ij}^{(k-1)}$
- $a_j^{(k-1)}$可能参与多条路径，需要累加
- 实际上，误差是$\sum_i \delta_i^{(k)} w_{ij}^{(k-1)}$
- $a_j^{(k-1)}$的误差为$f’(z_j^{(k-1)}) \sum_i \delta_i^{(k)} w_{ij}^{(k-1)}$
eg
向量化形态
为了提高计算效率，我们通常使用向量化形式进行批量计算。这种方式能够充分利用现代硬件的并行计算能力。
在实际神经网络训练中，常基于一批样本来更新网络权重。高效的方式是向量化，直接一次更新权值矩阵和偏置向量。
对于参数$W^{(k)}$，其梯度误差为：
$$
\nabla_{W^{(k)}} = \delta^{(k+1)} (a^{(k)})^T
$$
其中$\delta^{(k+1)}$是反向传播的误差向量，$a^{(k)}$是前向激活输出。
这样，整个矩阵形式的梯度就是误差向量和前向激活的外积。
- 矩阵形式的梯度计算：
- $\frac{\partial L}{\partial W} = \frac{1}{m} \sum_{i=1}^m \delta^{(i)} \cdot (x^{(i)})^T$，考虑所有样本的梯度
- $\frac{\partial L}{\partial b} = \frac{1}{m} \sum_{i=1}^m \delta^{(i)}$，偏置的批量更新
- 计算效率优化：
- 使用矩阵运算代替循环，提高计算速度
- 缓存中间结果，避免重复计算
- 批量处理，提高内存访问效率
深度神经网络
基础概念
深度神经网络通过多层非线性变换，能够学习更复杂的特征表示。每一层都从前一层提取更高层次的特征，最终形成层次化的特征表示。
- 网络结构：
- 输入层：$x \in \mathbb{R}^{n_0}$，原始输入数据
- 隐藏层：$h^{(l)} = \sigma(W^{(l)}h^{(l-1)} + b^{(l)})$，第l层的特征表示
- 输出层：$y = W^{(L)}h^{(L-1)} + b^{(L)}$，最终预测结果
- 前向传播：
- 第l层输入：$z^{(l)} = W^{(l)}h^{(l-1)} + b^{(l)}$，线性变换
- 第l层输出：$h^{(l)} = \sigma(z^{(l)})$，非线性激活
- 最终输出：$y = h^{(L)}$，网络预测
- 反向传播：
- 输出层误差：$\delta^{(L)} = \frac{\partial L}{\partial y} \odot \sigma’(z^{(L)})$，计算输出层梯度
- 隐藏层误差：$\delta^{(l)} = (W^{(l+1)})^T\delta^{(l+1)} \odot \sigma’(z^{(l)})$，误差反向传播
- 参数梯度：$\frac{\partial L}{\partial W^{(l)}} = \delta^{(l)}(h^{(l-1)})^T$，计算权重更新量
训练技巧
深度网络的训练需要特殊的技巧来确保稳定性和性能。这些技巧包括归一化、残差连接等，它们能够帮助网络更好地学习和收敛。
- 批量归一化：
- 计算均值：$\mu_B = \frac{1}{m}\sum_{i=1}^m x_i$，批次数据的均值
- 计算方差：$\sigma_B^2 = \frac{1}{m}\sum_{i=1}^m (x_i - \mu_B)^2$，批次数据的方差
- 归一化：$\hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$，标准化数据
- 缩放和平移：$y_i = \gamma \hat{x}_i + \beta$，可学习的参数调整
- 残差连接：
- 基本形式：$h^{(l)} = F(h^{(l-1)}) + h^{(l-1)}$，添加跳跃连接
- 梯度传播：$\frac{\partial L}{\partial h^{(l-1)}} = \frac{\partial L}{\partial h^{(l)}}(1 + \frac{\partial F}{\partial h^{(l-1)}})$，缓解梯度消失
- 层归一化：
计算均值：$\mu = \frac{1}{H}\sum_{i=1}^H x_i$，特征维度上的均值
计算方差：$\sigma^2 = \frac{1}{H}\sum_{i=1}^H (x_i - \mu)^2$，特征维度上的方差
归一化：$\hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}$，标准化特征
多模型集成，提高泛化能力
网络架构
不同的网络架构适用于不同的任务，包括卷积神经网络、循环神经网络等。
- 卷积神经网络：
- 卷积层：$h_{i,j} = \sum_{m,n} w_{m,n}x_{i+m,j+n} + b$，提取局部特征
- 池化层：$h_{i,j} = \max_{m,n} x_{i+m,j+n}$，降维和特征选择
- 全连接层：$h = \sigma(Wx + b)$，最终分类
- 循环神经网络：
- 基本RNN：$h_t = \sigma(W_{hh}h_{t-1} + W_{xh}x_t + b_h)$，处理序列数据
- LSTM：$f_t = \sigma(W_f[h_{t-1}, x_t] + b_f)$，长短期记忆
- GRU：$z_t = \sigma(W_z[h_{t-1}, x_t] + b_z)$，门控循环单元
- 注意力机制：
- 注意力分数：$e_{ij} = a(s_i, h_j)$，计算相关性
- 注意力权重：$\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_k \exp(e_{ik})}$，归一化权重
- 上下文向量：$c_i = \sum_j \alpha_{ij}h_j$，加权求和
技巧与概念
梯度检查
梯度检查是验证反向传播实现正确性的重要工具。通过比较数值梯度和解析梯度，我们可以确保梯度计算的准确性。
- 数值梯度近似方法：
- 中心差分公式：$\frac{\partial f}{\partial x} \approx \frac{f(x + h) - f(x - h)}{2h}$，提供更准确的梯度估计
- 前向差分公式：$\frac{\partial f}{\partial x} \approx \frac{f(x + h) - f(x)}{h}$，计算量较小但精度较低
- 梯度检验实现：
1 | def eval_numerical_gradient(f, x): |
正则化
正则化是防止过拟合的重要技术，通过限制模型复杂度来提高泛化能力。
- L1正则化：
- 损失函数：$J = L + \lambda \sum_w |w|$，增加权重绝对值的惩罚项
- 梯度更新：$w = w - \alpha(\frac{\partial L}{\partial w} + \lambda \cdot \text{sign}(w))$，权重更新时考虑L1正则化项
- 作用：促使权重稀疏化，有助于特征选择和模型压缩
- 特点：L1正则化会使部分权重变为0，适合高维稀疏特征场景
- L2正则化：
- 损失函数：$J = L + \frac{\lambda}{2} \sum_w w^2$，增加权重平方和的惩罚项
- 梯度更新：$w = w - \alpha(\frac{\partial L}{\partial w} + \lambda w)$，权重更新时考虑正则化项
- Frobenius范数：$||W||F = \sqrt{\sum{i=1}^m \sum_{j=1}^n |w_{ij}|^2}$，用于衡量权重矩阵的大小
- 正则化系数λ的选择：
- 太大：模型欠拟合，无法学习到数据特征
- 太小：模型过拟合，无法泛化到新数据
- 偏置项不参与正则化原因：
- 偏置项对模型复杂度影响小，主要影响决策边界的位置
- 偏置项不需要正则化也能学习到合适的值
随机失活Dropout
Dropout是一种强大的正则化技术，通过随机丢弃神经元来防止过拟合，提高模型的泛化能力。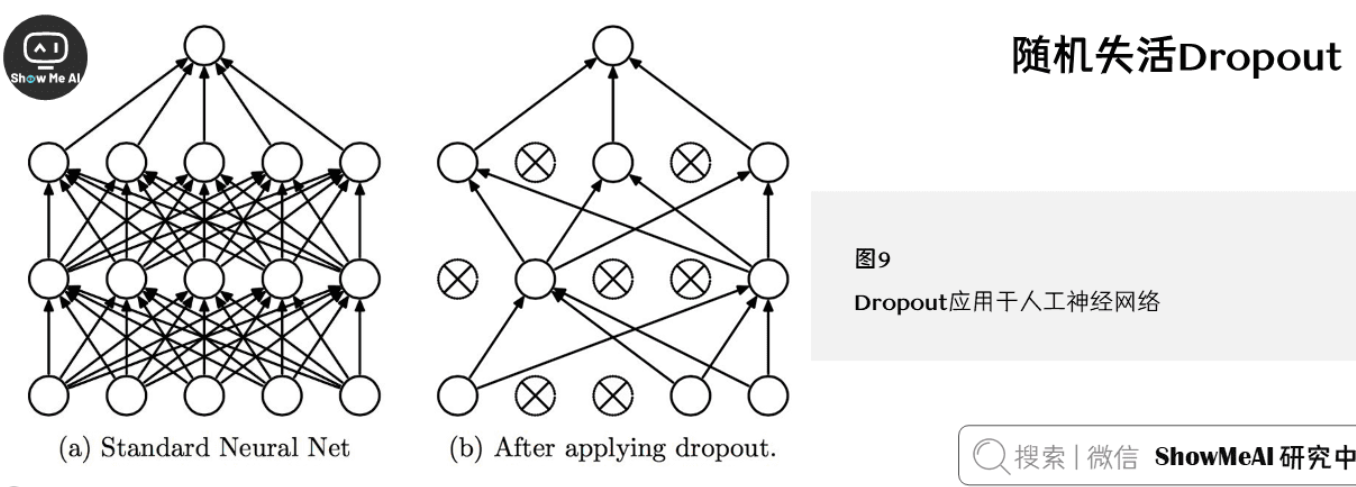
- Dropout原理：
- 训练时随机丢弃部分神经元，强制网络学习更鲁棒的特征
- 测试时使用全部神经元，但需要缩放输出
- 缩放因子：$1/(1-p)$，补偿训练时的丢弃
- 训练和测试阶段的处理：
- 训练：$h_{drop} = h \odot m, m \sim Bernoulli(p)$，随机mask
- 测试：$h_{test} = h \cdot (1-p)$，期望输出
- 集成学习解释：
- 每次dropout相当于训练一个子网络
- 最终模型相当于多个子网络的集成，提高泛化能力
- 贝叶斯学习解释：
- 可以看作是对参数的后验分布采样
- 每个子网络对应一个参数样本
- RNN中的变分Dropout：
- 对非循环连接进行dropout
- 在时间维度上保持相同的mask，保持时序一致性
激活函数
激活函数为神经网络引入非线性，使其能够学习复杂的模式。不同的激活函数适用于不同的场景。
- Sigmoid：
- 公式：$\sigma(x) = \frac{1}{1 + e^{-x}}$，将输入压缩到[0,1]区间
- 梯度：$\sigma’(x) = \sigma(x)(1-\sigma(x))$，在极端值处梯度接近0
- 特点：输出范围[0,1]，容易饱和，导致梯度消失
- tanh：
- 公式：$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$，将输入压缩到[-1,1]区间
- 梯度：$\tanh’(x) = 1 - \tanh^2(x)$，在0处梯度最大
- 特点：输出范围[-1,1]，零中心化，但仍有饱和问题
- hard tanh：
- 公式：$\mathrm{hardtanh}(x) = \begin{cases} -1 & x < -1 \ x & -1 \leq x \leq 1 \ 1 & x > 1 \end{cases}$，对输入进行截断，限制在[-1,1]区间
- 梯度：$\mathrm{hardtanh}’(x) = \begin{cases} 1 & -1 \leq x \leq 1 \ 0 & \text{otherwise} \end{cases}$，区间外梯度为0
- 特点：计算量小，数值会饱和（大于1或小于-1时恒为1或-1），有时比tanh更优选
- soft sign：
- 公式：$\mathrm{softsign}(x) = \frac{x}{1 + |x|}$，平滑地将输入压缩到(-1,1)区间
- 梯度：$\mathrm{softsign}’(x) = \frac{\mathrm{sgn}(x)}{(1 + |x|)^2}$，sgn为符号函数
- 特点：不会像hard clipped functions那样早饱和，平滑且零中心化，是tanh的另一种选择
- ReLU：
- 公式：$f(x) = \max(0, x)$，简单而有效
- 梯度：$f’(x) = \begin{cases} 1 & \text{if } x > 0 \ 0 & \text{if } x \leq 0 \end{cases}$，计算简单
- 特点：计算简单，缓解梯度消失，但可能出现死亡ReLU问题
- Leaky ReLU：
- 公式：$f(x) = \max(\alpha x, x), \alpha < 1$，允许负值梯度
- 梯度：$f’(x) = \begin{cases} 1 & \text{if } x > 0 \ \alpha & \text{if } x \leq 0 \end{cases}$，避免完全死亡
- 特点：解决死亡ReLU问题，保持负值信息
| 激活函数 | 输出范围 | 是否零中心 | 饱和性/梯度消失 | 计算复杂度 | 其他优缺点/适用场景 |
|---|---|---|---|---|---|
| Sigmoid | (0, 1) | 否 | 极易饱和，梯度消失严重 | 较高 | 早期常用，输出非零中心，易导致梯度消失，训练深层网络效果差，适合二分类输出层 |
| tanh | (-1, 1) | 是 | 饱和，梯度消失 | 较高 | 零中心化，收敛快于Sigmoid，但深层仍有梯度消失问题 |
| hard tanh | [-1, 1] | 是 | 区间外恒定，区间内线性，区间外梯度为0 | 极低 | 计算量小，数值易饱和，适合对计算资源要求高的场景，有时可替代tanh |
| soft sign | (-1, 1) | 是 | 不易早饱和，梯度平滑 | 较低 | 平滑零中心，梯度变化缓慢，适合需要平滑激活的场景，是tanh的替代选择 |
| ReLU | [0, +∞) | 否 | x<0时梯度为0，易”死亡” | 极低 | 计算简单，缓解梯度消失，收敛快，广泛用于深层网络，但有死亡ReLU问题 |
| Leaky ReLU | (-∞, +∞) | 否 | x<0时梯度为α，避免死亡 | 极低 | 保持负值信息，解决死亡ReLU，适合深层网络，α需调参 |
数据预处理
数据预处理是提高模型性能的关键步骤，通过标准化和归一化使数据更适合神经网络学习。
- 去均值：
- 计算训练集均值：$\mu = \frac{1}{m}\sum_{i=1}^m x^{(i)}$，中心化数据
- 减去均值：$x = x - \mu$，使数据分布以0为中心
- 归一化：
- 计算标准差：$\sigma = \sqrt{\frac{1}{m}\sum_{i=1}^m (x^{(i)} - \mu)^2}$，衡量数据分散程度
- 归一化：$x = \frac{x - \mu}{\sigma}$，使数据分布更加均匀
- 白化：
- 计算协方差矩阵：$\Sigma = \frac{1}{m}\sum_{i=1}^m (x^{(i)} - \mu)(x^{(i)} - \mu)^T$，描述特征间关系
- 特征值分解：$\Sigma = U\Lambda U^T$，获取主成分
- 白化：$x_{white} = U\Lambda^{-1/2}U^Tx$，消除特征间相关性
参数初始化
参数初始化对神经网络的训练至关重要，好的初始化可以加速收敛并提高模型性能。
- Xavier初始化：
- 均匀分布：$W \sim U(-\sqrt{\frac{6}{n_{in} + n_{out}}}, \sqrt{\frac{6}{n_{in} + n_{out}}})$，保持方差
- 正态分布：$W \sim N(0, \sqrt{\frac{2}{n_{in} + n_{out}}})$，高斯分布版本
- 保持激活方差和梯度方差：
- 输入方差：$\text{Var}(x) = 1$，标准化输入
- 输出方差：$\text{Var}(y) = 1$，保持信号强度
- 权重方差：$\text{Var}(W) = \frac{2}{n_{in} + n_{out}}$，防止梯度消失/爆炸
学习策略
学习策略决定了模型如何从数据中学习，包括学习率的选择和调整方法。
- 学习率选择：
- 初始学习率：$\alpha_0 = 0.01$，常用起始值
- 验证集调优，找到最佳学习率
- 学习率衰减：
- 步长衰减：$\alpha = \alpha_0 \cdot \gamma^{\lfloor t/s \rfloor}$，定期降低学习率
- 指数衰减：$\alpha = \alpha_0 \cdot e^{-kt}$，平滑降低
- 时间衰减：$\alpha = \frac{\alpha_0}{1 + kt}$，渐进式降低
- 学习率预热：
- 线性预热：$\alpha = \alpha_0 \cdot \min(1, t/T)$，逐步增加学习率
- 余弦预热：$\alpha = \alpha_0 \cdot \frac{1}{2}(1 + \cos(\pi(1 - t/T)))$，平滑过渡
优化算法
总览
优化算法是神经网络训练的核心，它们决定了模型如何从数据中学习。
- 优化目标：
- 最小化损失函数：$\min_\theta L(\theta)$，找到最优参数
- 参数更新：$\theta_{t+1} = \theta_t - \alpha_t \nabla L(\theta_t)$，梯度下降
- 优化算法分类：
- 一阶优化：梯度下降及其变体，计算简单
- 二阶优化：牛顿法、拟牛顿法，收敛更快
- 自适应优化：根据参数特性调整学习率
梯度下降
梯度下降是最基本的优化算法，有多种变体以适应不同场景。
- 批量梯度下降(BGD)：
- 更新规则：$\theta_{t+1} = \theta_t - \alpha \frac{1}{m}\sum_{i=1}^m \nabla L_i(\theta_t)$，使用所有样本
- 特点：计算准确但计算量大，适合小数据集
- 随机梯度下降(SGD)：
- 更新规则：$\theta_{t+1} = \theta_t - \alpha \nabla L_i(\theta_t)$，使用单个样本
- 特点：计算快但噪声大，适合大规模数据
- 小批量梯度下降(MBGD)：
- 更新规则：$\theta_{t+1} = \theta_t - \alpha \frac{1}{b}\sum_{i=1}^b \nabla L_i(\theta_t)$，使用小批量样本
- 特点：平衡计算效率和收敛性，最常用
动量优化
动量方法通过累积历史梯度来加速收敛，减少震荡，提高训练稳定性。
- 标准动量：
- 速度更新：$v_t = \gamma v_{t-1} - \alpha \nabla L(\theta_t)$，累积梯度
- 参数更新：$\theta_{t+1} = \theta_t + v_t$，更新参数
- 特点：加速收敛，减少震荡，提高稳定性
- Nesterov动量：
- 速度更新：$v_t = \gamma v_{t-1} - \alpha \nabla L(\theta_t + \gamma v_{t-1})$，提前计算梯度
- 参数更新：$\theta_{t+1} = \theta_t + v_t$，更新参数
- 特点：更准确的方向，收敛更快
- 动量方法原理：
- 累积历史梯度，形成”惯性”
- 减少震荡，使优化路径更平滑
- 加速收敛，特别是在平坦区域
- 实现伪代码：
1 | def sgd_momentum(w, dw, config=None): |
自适应学习率优化
自适应优化算法能够根据参数特性自动调整学习率，提高训练效率。
- AdaGrad：
- 累积平方梯度：$G_t = G_{t-1} + g_t^2$，记录历史梯度
- 更新规则：$\theta_t = \theta_{t-1} - \frac{\alpha}{\sqrt{G_t + \epsilon}} \odot g_t$，自适应学习率
- 特点：适合稀疏数据，但学习率衰减快
- RMSProp：
- 移动平均：$G_t = \beta G_{t-1} + (1-\beta)g_t^2$，指数移动平均
- 更新规则：$\theta_t = \theta_{t-1} - \frac{\alpha}{\sqrt{G_t + \epsilon}} \odot g_t$，动态调整
- 特点：解决AdaGrad学习率衰减问题，保持长期记忆
- Adam：
- 一阶矩：$m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t$，梯度一阶矩
- 二阶矩：$v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2$，梯度二阶矩
- 偏差修正：$\hat{m}_t = \frac{m_t}{1-\beta_1^t}, \hat{v}_t = \frac{v_t}{1-\beta_2^t}$，修正初始偏差
- 更新规则：$\theta_t = \theta_{t-1} - \frac{\alpha}{\sqrt{\hat{v}_t} + \epsilon} \odot \hat{m}_t$，结合动量和自适应
- 特点：结合动量和自适应学习率的优点，最常用
二阶优化方法
二阶优化方法利用Hessian矩阵信息，收敛更快但计算成本高。
- 牛顿法：
- 更新规则：$\theta_{t+1} = \theta_t - H^{-1}\nabla L(\theta_t)$，使用Hessian矩阵
- 特点：收敛快但计算Hessian矩阵代价大
- 拟牛顿法：
- BFGS算法，近似Hessian矩阵
- L-BFGS算法，限制内存使用
- 特点：近似Hessian矩阵，降低计算复杂度
优化算法改进
为了进一步提高优化效果，可以采用各种改进策略。
- 梯度裁剪：
- 阈值裁剪：$g = g \cdot \min(1, \frac{\theta}{||g||})$，限制梯度范数
- 范数裁剪：$g = g \cdot \min(1, \frac{\theta}{||g||_2})$，L2范数裁剪
- 学习率调度：
- 循环学习率：$\alpha_t = \alpha_{min} + \frac{1}{2}(\alpha_{max} - \alpha_{min})(1 + \cos(\frac{t}{T}\pi))$，周期性调整
- 余弦退火：$\alpha_t = \alpha_{min} + \frac{1}{2}(\alpha_{max} - \alpha_{min})(1 + \cos(\frac{t}{T}\pi))$，平滑降低
- 早停策略：
- 验证集监控，防止过拟合
- 耐心参数设置，容忍性能波动
- 最佳模型保存，记录最优结果
方法比较
不同优化算法有各自的优缺点，需要根据具体问题选择。
- 收敛速度：
- 一阶方法：线性收敛，计算简单
- 二阶方法：二次收敛，计算复杂
- 自适应方法：超线性收敛，平衡效率和效果
- 内存消耗：
- SGD：最小，适合大规模数据
- Adam：中等，需要存储动量
- 二阶方法：最大，需要存储Hessian
- 适用场景：
- 小数据集：SGD + 动量，稳定可靠
- 大数据集：Adam，自适应高效
- 特殊任务：特定优化器，根据需求选择
代码实现
1 | # SGD with Momentum |
发展趋势
优化算法领域正在不断发展，涌现出许多新的研究方向。
- 自适应优化：
- 动态学习率，根据训练过程调整
- 参数特定学习率，针对不同参数
- 自适应批量大小，动态调整批量
- 分布式优化：
- 数据并行，处理大规模数据
- 模型并行，处理大模型
- 混合并行，结合多种并行策略
- 优化算法理论：
- 收敛性分析，理论保证
- 稳定性研究，提高可靠性
- 泛化性分析，提高模型性能
实践流程
模型训练流程
- 数据准备：
- 数据清洗和预处理
- 数据集划分（训练集、验证集、测试集）
- 数据增强和标准化
- 模型构建：
- 网络架构设计
- 层数和神经元数量选择
- 激活函数选择
- 训练过程：
- 参数初始化
- 优化器选择
- 学习率设置
- 批量大小确定
- 模型评估：
- 训练集和验证集性能监控
- 过拟合检测
- 模型调优
超参数调优
- 网格搜索：
- 参数空间定义
- 搜索策略
- 评估指标选择
- 随机搜索：
- 参数分布设置
- 采样策略
- 资源分配
- 贝叶斯优化：
- 代理模型构建
- 采集函数选择
- 参数更新策略
- 自动化调优：
- 早停策略
- 学习率自适应
- 批量大小动态调整
评估与验证
- 评估指标：
- 准确率、精确率、召回率
- F1分数、ROC曲线
- 混淆矩阵
- 交叉验证：
- K折交叉验证
- 留一法
- 分层抽样
- 模型比较：
- 统计显著性检验
- 模型复杂度分析
- 计算资源消耗
部署与优化
- 模型压缩：
- 知识蒸馏
- 模型剪枝
- 量化技术
- 推理优化：
- 批处理
- 模型并行
- 硬件加速
- 部署策略：
- 模型版本控制
- 服务监控
- 性能优化
问题与解决
- 过拟合：
- 增加训练数据
- 使用正则化
- 早停策略
- Dropout
- 欠拟合：
- 增加模型复杂度
- 减少正则化强度
- 调整学习率
- 梯度问题：
- 梯度消失：使用ReLU、残差连接
- 梯度爆炸：梯度裁剪、权重初始化
- 训练不稳定：
- 批量归一化
- 学习率预热
- 优化器选择
代码示例
1 | # 模型训练流程 |