参考:
语言模型
概念
语言模型(Language Model)是计算一个句子概率的模型,即计算一个句子出现的可能性。对于句子 $S = (w_1, w_2, …, w_m)$,其概率可以表示为:
$$P(S) = P(w_1, w_2, …, w_m)$$
这个概率可以进一步分解为条件概率的乘积:
$$P(S) = P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)…P(w_m|w_1,w_2,…,w_{m-1})$$
这种分解方式反映了语言中的顺序性和上下文依赖性。语言模型的核心任务就是估计这些条件概率。
评估
评估语言模型的质量通常使用以下指标:
困惑度(Perplexity):评估语言模型质量的重要指标,值越小表示模型越好
$$PP(W) = \sqrt[N]{\prod_{i=1}^N \frac{1}{P(w_i|w_1, …, w_{i-1})}}$$困惑度可以理解为模型在预测下一个词时的平均分支数。例如,如果困惑度为100,意味着模型在预测下一个词时平均有100个可能的选择。
交叉熵(Cross Entropy):与困惑度相关,是更基础的评估指标
$$H(W) = -\frac{1}{N}\sum_{i=1}^N \log P(w_i|w_1, …, w_{i-1})$$交叉熵反映了模型预测分布与真实分布之间的差异,值越小表示模型预测越准确。
N-gram语言模型
概念
N-gram模型基于马尔可夫假设,即当前词只依赖于前N-1个词。这个假设大大简化了语言模型的复杂度:
$$P(w_t|w_1, w_2, …, w_{t-1}) \approx P(w_t|w_{t-n+1}, …, w_{t-1})$$
例如,对于bigram模型(n=2):
$$P(w_t|w_1, w_2, …, w_{t-1}) \approx P(w_t|w_{t-1})$$
对于trigram模型(n=3):
$$P(w_t|w_1, w_2, …, w_{t-1}) \approx P(w_t|w_{t-2}, w_{t-1})$$
对于N-gram模型,概率计算公式为:
$$P(w_t|w_{t-n+1}, …, w_{t-1}) = \frac{count(w_{t-n+1}, …, w_t)}{count(w_{t-n+1}, …, w_{t-1})}$$
这个公式基于最大似然估计(MLE)原理。例如,对于bigram模型:
$$P(w_t|w_{t-1}) = \frac{count(w_{t-1}, w_t)}{count(w_{t-1})}$$
特点
优点
- 简单直观,易于实现
- 只需统计有限长度的上下文
- 在小规模任务和数据量足够时效果较好
缺点
- 维度灾难:
- $n$ 增大时,参数数量指数级增长随着n增大,泛化能力的优势会减弱。
- 在$n$过小时,n-gram 难以承载足够的语言信息,不足以反应语料库的特性。
- 稀疏性问题:很多n-gram组合在语料中未出现,概率为0(“零概率” 现象→通过平滑(Smoothing) 技术进行改善)
- 只能捕捉有限长度的上下文,无法建模长距离依赖
- 需要大量存储和计算全局统计信息
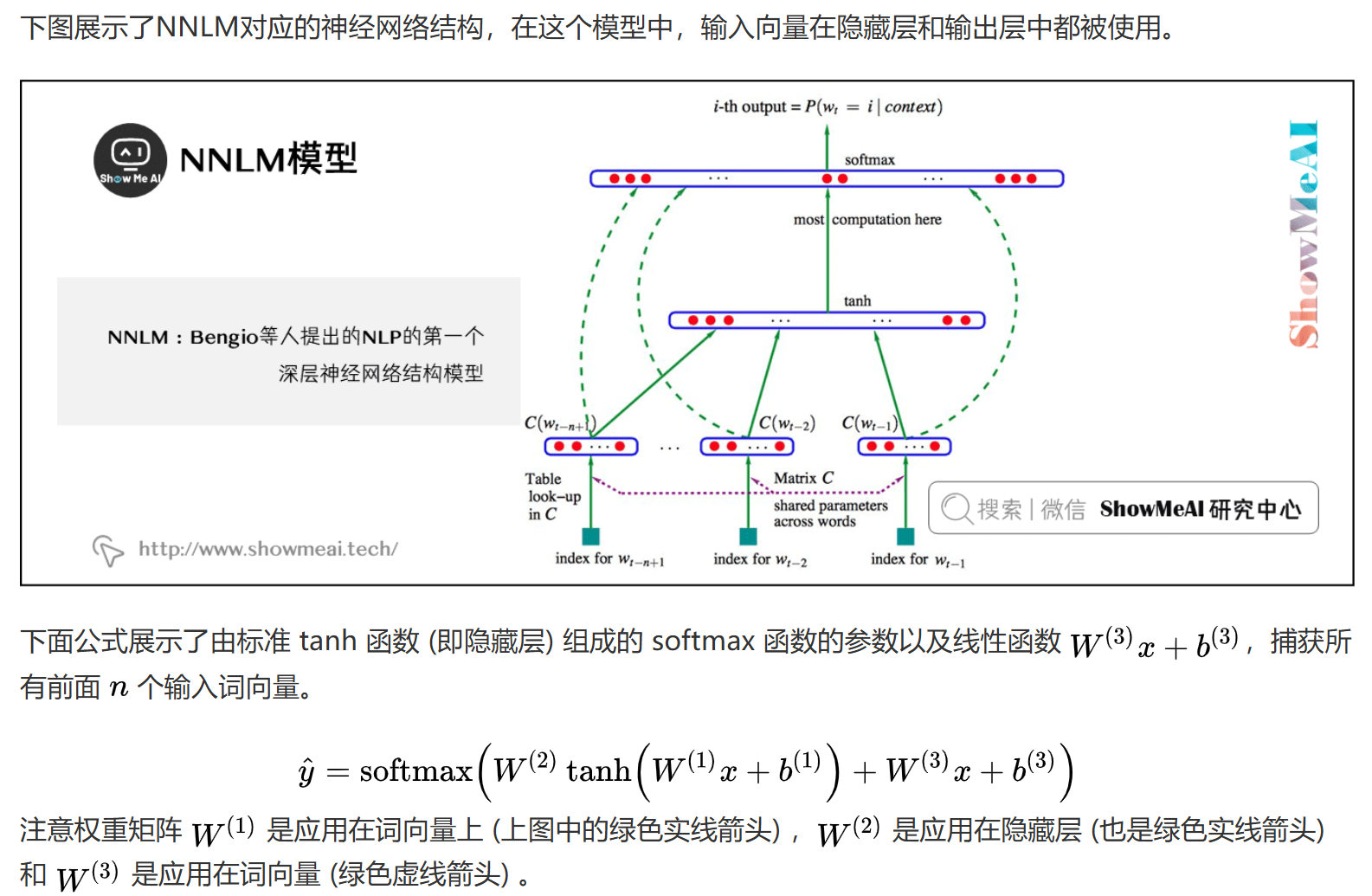
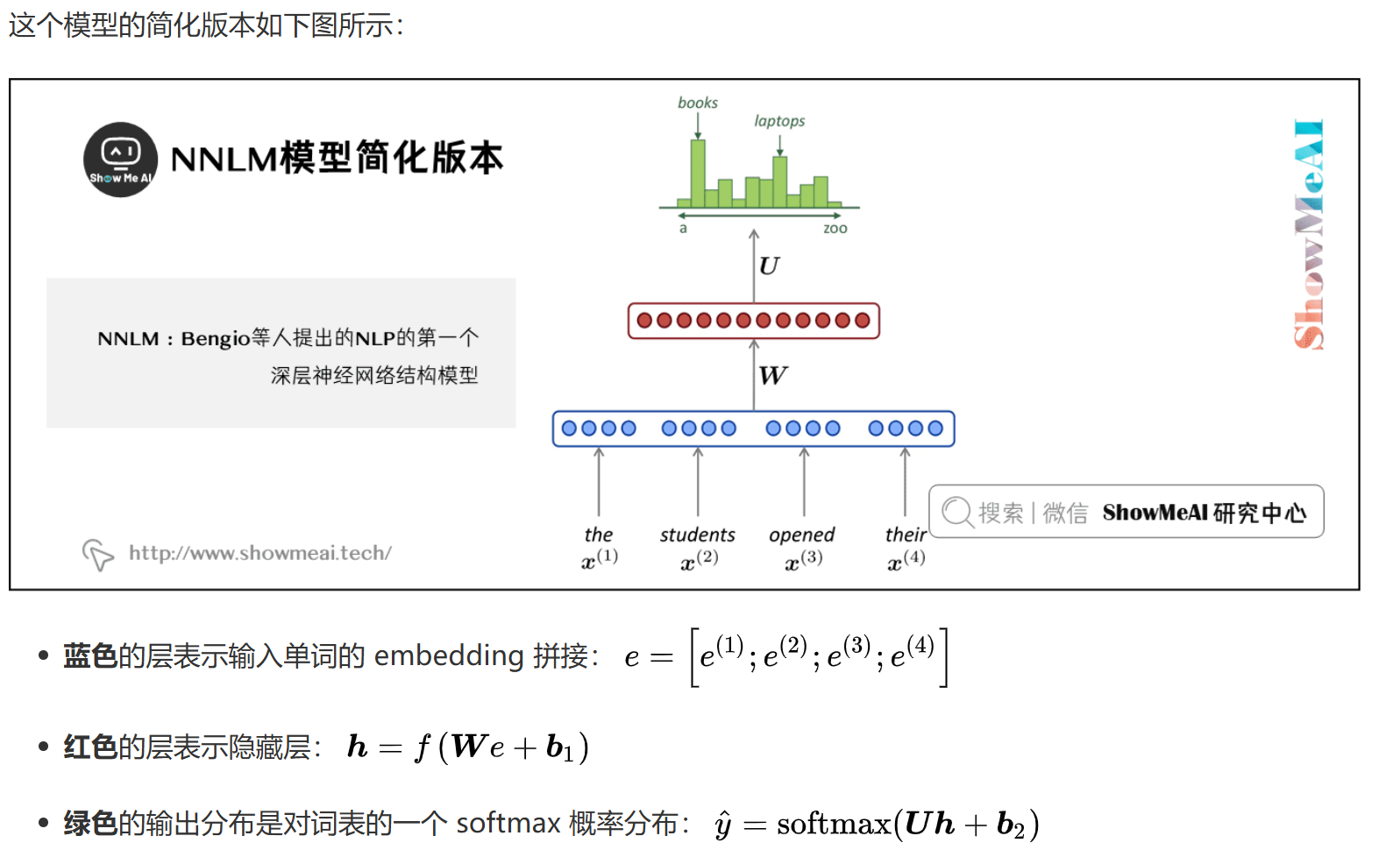
NNLM
模型结构
NNLM通过神经网络来学习词的概率分布,主要包含三个部分:
- 输入层:词嵌入,将词转换为密集向量
- 隐藏层:非线性变换,捕捉词序列的特征
- 输出层:softmax分类,预测下一个词的概率
词嵌入层
词嵌入层是NNLM的重要组成部分:
- 将词转换为密集向量表示,维度通常为50-300
- 可以捕捉词的语义信息,相似词有相似的向量表示
- 通过训练学习得到,不需要人工标注
- 支持词的类比关系,如:king - man + woman ≈ queen
数学表示
对于输入序列 $(w_1, w_2, …, w_{t-1})$,预测下一个词 $w_t$ 的概率:
$$P(w_t|w_1, w_2, …, w_{t-1}) = softmax(W_2 \cdot tanh(W_1 \cdot [E(w_1), …, E(w_{t-1})] + b_1) + b_2)$$
其中:
- $E(w_i)$ 是词 $w_i$ 的嵌入向量
- $W_1, W_2$ 是权重矩阵
- $b_1, b_2$ 是偏置向量
- $tanh$ 是激活函数
- $softmax$ 将输出转换为概率分布
特点
超越 n-gram 语言模型的改进:
- 没有稀疏性问题
- 不需要观察到所有的n-grams
NNLM存在的问题:
- 固定窗口太小
- 扩大窗口就需要扩大权重矩阵公式
- 窗口再大也不够用
- $x^{(1)}$ 和 $x^{(2)}$ 乘以完全不同的权重。输入的处理不对称→需要一个神经结构,可以处理任何长度的输入
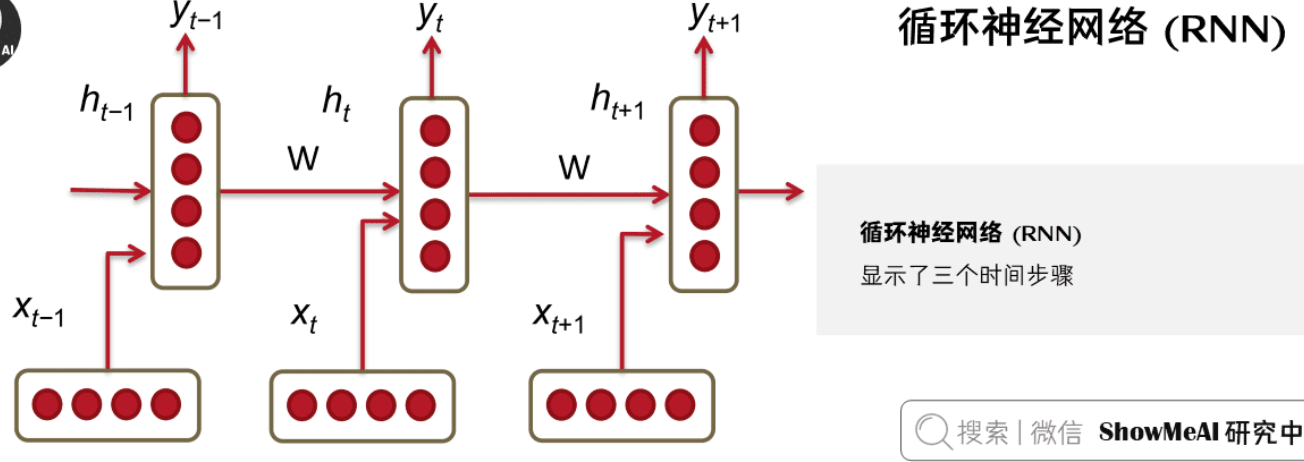
循环神经网络RNN
基本结构
传统的统计翻译模型,只能以有限窗口大小的前n个单词作为条件进行语言模型建模,循环神经网络与其不同,RNN 有能力以语料库中所有前面的单词为条件进行语言模型建模。
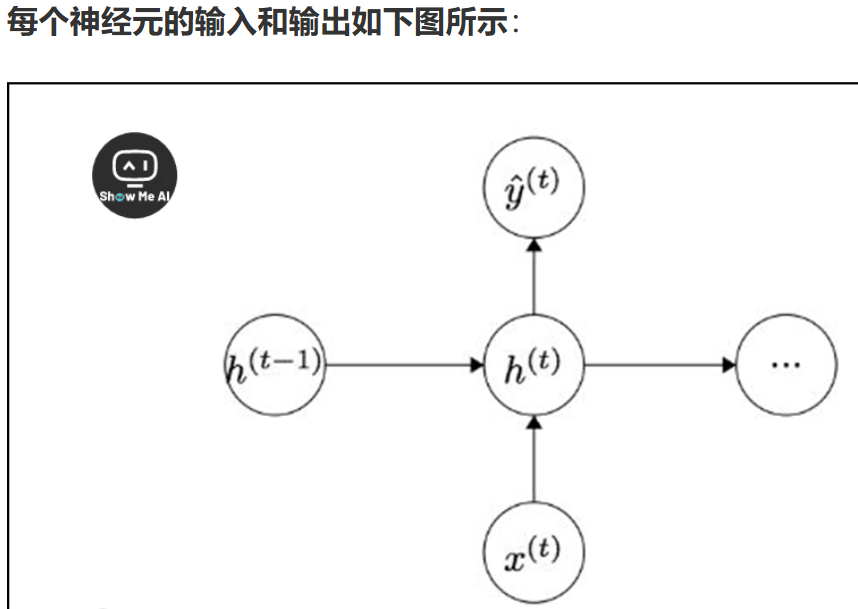
RNN通过循环连接处理序列数据,其核心思想是使用同一个网络处理序列中的每个元素。隐藏状态更新公式:
$$h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t + b_h)$$
其中:
- $h_t$ 是当前时刻的隐藏状态
- $h_{t-1}$ 是上一时刻的隐藏状态
- $x_t$ 是当前时刻的输入
- $W_{hh}, W_{xh}$ 是权重矩阵
- $b_h$ 是偏置向量
- $tanh$ 是激活函数
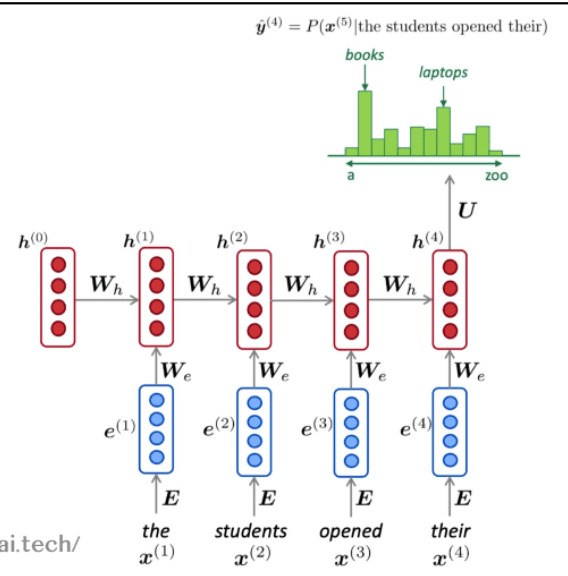
输出计算
RNN的输出计算:
$$y_t = W_{hy}h_t + b_y$$
其中:
- $y_t$ 是当前时刻的输出
- $W_{hy}$ 是输出层的权重矩阵
- $b_y$ 是输出层的偏置向量
损失函数
对于序列预测任务,损失函数通常为交叉熵:
$$L = -\sum_{t=1}^T \sum_{c=1}^C y_{t,c} \log(\hat{y}_{t,c})$$
其中:
- $T$ 是序列长度
- $C$ 是类别数(词汇表大小)
- $y_{t,c}$ 是真实标签
- $\hat{y}_{t,c}$ 是模型预测的概率
RNN的变体
双向RNN
BiRNN
概念
前面部分是用 RNN 如何使用过去的词来预测序列中的下一个单词。同理,可以通过令 RNN 模型向反向读取语料库,根据未来单词进行预测。BiRNN使用前向后向RNN分别获取双向(上下文)信息再合并。
Irsoy 等人展示了一个双向深度神经网络;在每个时间步t,这个网络维持两个隐藏层,一个是从左到右传播,而另外一个是从右到左传播。
为了在任何时候维持两个隐藏层,该网络要消耗的两倍存储空间来存储权值和偏置参数。最后的分类结果 $\hat y$ ,是结合由两个 RNN 隐藏层生成的结果得分产生。
数学定义
$$h_t^f = tanh(W_{hh}^f h_{t-1}^f + W_{xh}^f x_t + b_h^f)$$
$$h_t^b = tanh(W_{hh}^b h_{t+1}^b + W_{xh}^b x_t + b_h^b)$$
$$h_t = [h_t^f; h_t^b]$$
多层RNN
Deep RNN
概念
多层RNN(Deep RNN)通过堆叠多个RNN层,提升模型的表达能力和抽象能力。每一层的输出作为下一层的输入,能够捕捉更复杂的时序特征。
结构与原理
- 多层RNN将多个RNN单元按层级堆叠,底层捕捉低级特征,高层捕捉高级抽象。
- 增加深度有助于模型学习更复杂的序列关系,但也会带来梯度消失/爆炸等训练难题。
数学定义
设有$L$层RNN,第$l$层的隐藏状态为$h_t^{(l)}$,则:
$$
h_t^{(1)} = \text{RNN}^{(1)}(x_t, h_{t-1}^{(1)})
$$
$$
h_t^{(l)} = \text{RNN}^{(l)}(h_t^{(l-1)}, h_{t-1}^{(l)}), \quad l=2,3,…,L
$$
最终输出可由最后一层隐藏状态给出。
残差连接RNN
Residual RNN
概念
残差连接RNN在多层RNN的基础上引入跨层的跳跃连接(Residual/Skip Connection),缓解深层网络中的梯度消失问题。
结构与原理
- 在每一层RNN的输出中,加入前一层的输出作为残差项。
- 这样可以为梯度提供直接的传播路径,使深层RNN更易训练。
数学定义
以两层RNN为例,残差连接形式为:
$$
h_t^{(2)} = \text{RNN}^{(2)}(h_t^{(1)}, h_{t-1}^{(2)}) + h_t^{(1)}
$$
更一般地,对于第$l$层:
$$
h_t^{(l)} = \text{RNN}^{(l)}(h_t^{(l-1)}, h_{t-1}^{(l)}) + h_t^{(l-1)}
$$
说明
- 残差连接有助于缓解深层RNN的训练难题,提升模型性能。
- 该思想最早在ResNet中提出,现已广泛应用于RNN、Transformer等结构。
RNN的局限性
梯度消失/爆炸问题:长序列训练时,梯度可能变得极小或极大
长期依赖问题:难以捕捉长距离的依赖关系,太远的效果差
计算效率问题:计算速度很慢——因为它每一个时间步需要依赖上一个时间步,所以不能并行化,序列处理是串行的→Transformer
梯度消失与爆炸
实验现象
- 梯度爆炸时,训练过程中loss会突然变为NaN或极大。
- 梯度消失时,loss长期不下降,模型无法学习长距离依赖。
导致问题
梯度消失:
- 1.在反向传播的阶段的过程中,从前面时间步中回传过来的梯度值会逐渐消失。因此,对于长句子,预测到空白处的答案的概率会随着上下文信息增大而减少。
- 来自远处的梯度信号会丢失,因为它比来自近处的梯度信号小得多。
- 因此,模型权重只会根据近期效应而不是长期效应进行更新。
- 2.梯度可以被看作是过去对未来的影响的衡量标准
- 如果梯度很小,模型就不能学习这种依赖关系。
- 1.在反向传播的阶段的过程中,从前面时间步中回传过来的梯度值会逐渐消失。因此,对于长句子,预测到空白处的答案的概率会随着上下文信息增大而减少。
梯度爆炸:
- 如果梯度过大,则SGD更新步骤过大
- 这可能导致错误的更新:我们更新的太多,导致错误的参数配置(损失很大)
- 在最坏的情况下,这将导致网络中的 Inf 或 NaN(然后你必须从较早的检查点重新启动训练)
数学原理
RNN在反向传播时,损失对参数$W$的梯度为:
$$
\frac{\partial E}{\partial W} = \sum_{i=1}^T \frac{\partial E_i}{\partial W}
$$
即每个时间步的误差累加。
以标准RNN为例,隐藏状态递推:
$$
h_t = \sigma\left(W^{(hh)} h_{t-1} + W^{(hx)} x_{[t]}\right)
$$
输出层:
$$
\hat{y}_t = \text{softmax}(W^{(S)} h_t)
$$
对$h_t$关于$h_k$的偏导数递推:
$$
\frac{\partial h_t}{\partial h_k} = \prod_{j=k+1}^t W^{(hh)T} \cdot \text{diag}\left[\sigma’(h_{j-1})\right]
$$
Jacobian矩阵的元素为:
$$
\frac{\partial h_j}{\partial h_{j-1}} = W^{(hh)T} \cdot \text{diag}\left[\sigma’(h_{j-1})\right]
$$
最终梯度表达式:
$$
\frac{\partial E}{\partial W} = \sum_{t=1}^T \sum_{k=1}^t \frac{\partial E_t}{\partial y_t} \frac{\partial y_t}{\partial h_t} \left(\prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}}\right) \frac{\partial h_k}{\partial W}
$$
范数分析
对链式法则中的Jacobian矩阵范数进行分析:
$$
\left|\frac{\partial h_t}{\partial h_k}\right| \leq \prod_{j=k+1}^t \left|W^{(hh)T}\right| \cdot \left|\text{diag}(\sigma’(h_{j-1}))\right|
$$
设$\beta_W = |W^{(hh)T}|$,$\beta_h = \max_j |\text{diag}(\sigma’(h_{j-1}))|$,则:
$$
\left|\frac{\partial h_t}{\partial h_k}\right| \leq (\beta_W \beta_h)^{t-k}
$$
- 当$\beta_W \beta_h < 1$时,梯度指数级衰减,导致梯度消失。
- 当$\beta_W \beta_h > 1$时,梯度指数级增长,导致梯度爆炸。
这就是RNN在长序列训练时,早期时间步的梯度难以有效传递到前面,或者出现数值溢出的根本原因。
解决方法
梯度爆炸
梯度裁剪(Gradient Clipping)
当梯度范数超过阈值时,按比例缩放:
$$
\hat{g} = \frac{\partial E}{\partial W}
$$
$$
\text{if } |\hat{g}| > \text{threshold} \text{ then } \hat{g} \leftarrow \frac{\text{threshold}}{|\hat{g}|} \hat{g}
$$
这种方法可以有效防止梯度爆炸导致的数值不稳定(如NaN),在实际训练RNN/LSTM时非常常用。
梯度消失
- 权重初始化为单位矩阵:$W^{(hh)}$初始化为单位矩阵,保证初始时$\beta_W \approx 1$,缓解长链路梯度消失。
- 使用ReLU激活:ReLU的导数为$0$或$1$,相比sigmoid/tanh更不易梯度消失。
- 残差连接:在RNN中引入残差连接(如 $h_t = F(h_{t-1}, x_t) + h_{t-1}$ ),为梯度提供直接路径。
- LSTM/GRU结构:通过门控机制为梯度提供”捷径”,有效缓解梯度消失。
问题泛化
- 梯度消失/爆炸只是RNN问题吗?
并不是,这对于所有的神经结构(包括前馈和卷积网络) 都是一个问题,尤其是对于深度结构
由于链式法则/选择非线性函数,反向传播时梯度可以变得很小。
因此,较低层次的学习非常缓慢(难以训练)。
- 解决方案:大量新的深层前馈 / 卷积架构,添加更多的直接连接(从而使梯度可以流动)
例如:
- 残差连接ResNet
默认情况下,标识连接保存信息
这使得深层网络更容易训练
“Deep Residual Learning for Image Recognition”, He et al, 2015.
- 密集连接DenseNet
直接将所有内容连接到所有内容
“Densely Connected Convolutional Networks”, Huang et al, 2017.
- 高速网络Highway
类似于残差连接,但标识连接与转换层由动态门控制
灵感来自LSTMs,但适用于深度前馈/卷积网络
“Highway Networks”, Srivastava et al, 2015.
结论:虽然梯度消失/爆炸是一个普遍的问题,但由于重复乘以相同的权矩阵,RNN尤其不稳定。
“Learning Long-Term Dependencies with Gradient Descent is Difficult”, Bengio et al. 1994.
长短期记忆网络LSTM
核心组件
LSTM通过三个门控机制解决RNN的问题:
遗忘门:控制丢弃信息
输入门:控制新信息存储
输出门:控制信息输出
新单元内容:这是要写入单元的新内容
单元状态:删除(“忘记”)上次单元状态中的一些内容,并写入(“输入”)一些新的单元内容
隐藏状态:【区别于RNN的重要特征】从单元中读取(“output”)一些内容。它能保存长期记忆,包含有关到目前为止已处理的序列的信息,并在每个时间步长更新。隐藏状态对于跨时间步长和层维护信息至关重要。
nn.LSTM中的hidden_size指的是每个时间步输出的h的长度。
(以上6个都是长度相同(公式)的向量)
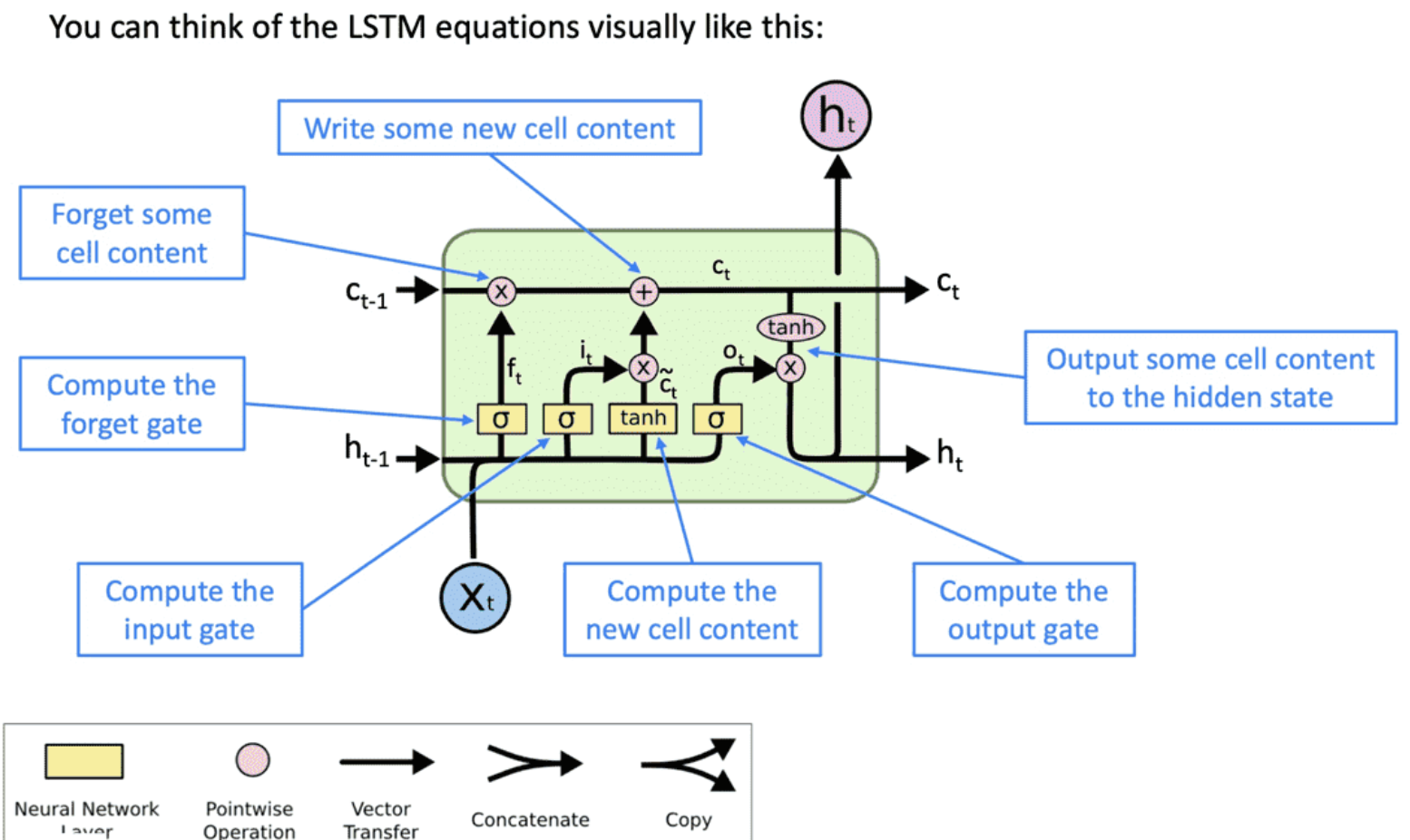
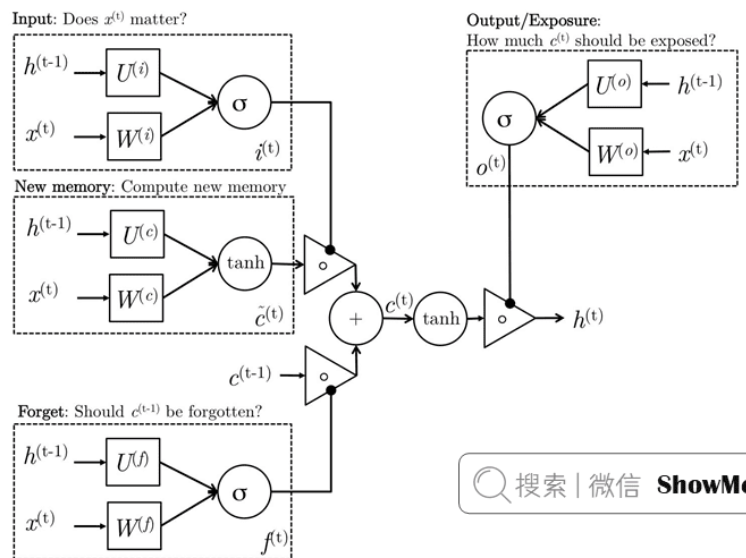
数学表示
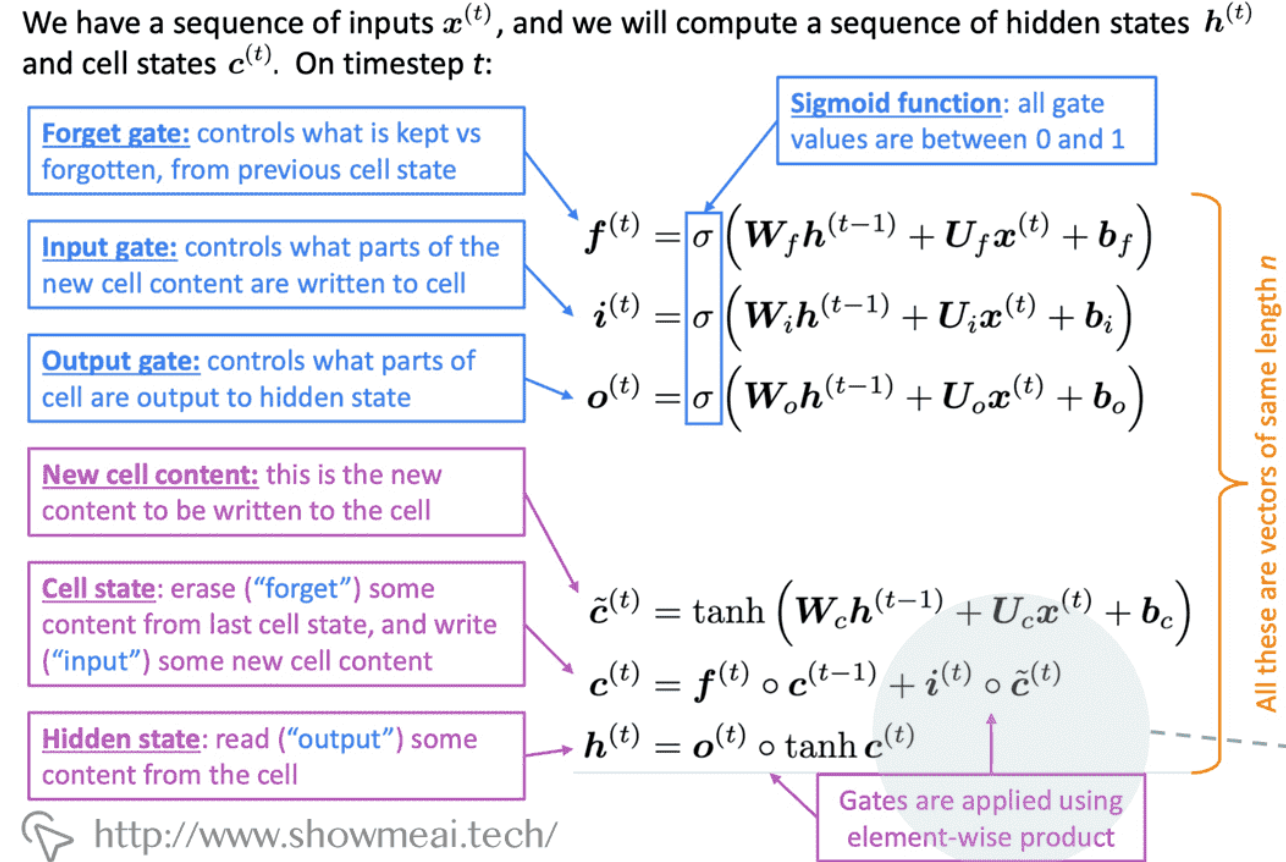
遗忘门:
$$f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)$$输入门:
$$i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)$$
$$\tilde{C}_t = tanh(W_C \cdot [h_{t-1}, x_t] + b_C)$$输出门:
$$o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)$$单元状态更新:
$$C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$$隐藏状态更新:
$$h_t = o_t \odot tanh(C_t)$$
其中:
- $\sigma$ 是sigmoid函数
- $\odot$ 表示逐元素乘法
- $C_t$ 是单元状态
- $h_t$ 是隐藏状态
激活函数
sigmoid
Sigmoid函数的输出范围是(0, 1),非常适合用于门控机制。
在LSTM中,sigmoid用于遗忘门、输入门和输出门。这些门控需要决定信息是否通过,sigmoid的输出恰好可以表示这种概率或比例,当输入极端时,输出接近0或1,实现”关闭”或”完全开启”的效果。Sigmoid的饱和性确保门控状态稳定,避免梯度剧烈变化
tanh
Tanh函数的输出范围是(-1, 1),适合用于表示一个值的范围或幅度(状态)。
在LSTM中,tanh用于初始化细胞状态的候选值和最终的细胞状态及隐藏状态的计算。这些状态需要表示实际的值,而不仅仅是开启或关闭的比例,因此tanh可以提供更丰富的信息。Tanh的输出范围对称且梯度更稳定,有助于缓解梯度消失问题。
消融实验
为了探究LSTM中各部分作用,谷歌做了一个消融实验。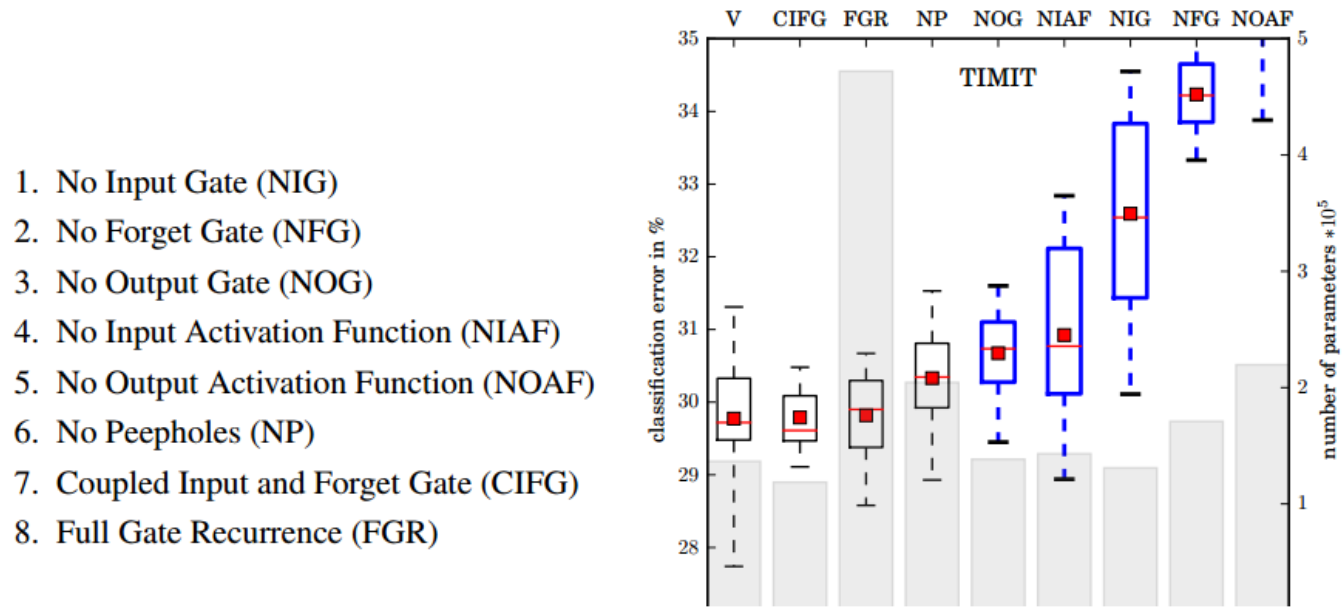
结果:
- 标准LSTM:各门控和激活函数齐全时,性能最佳,分类错误率最低。
- 耦合输入和遗忘门(CIFG):将输入门和遗忘门合并,参数减少,性能略有下降,但仍接近标准LSTM。→GRU
- 无窥视孔(NP):去除peephole连接,对性能影响较小,说明peephole不是关键结构。
- 无输出门(NOG)/无输入门(NIG)/无遗忘门(NFG):去除任一主要门控,错误率显著上升,尤其是去除遗忘门(NFG)影响最大,说明遗忘门对LSTM性能至关重要。
- 无输入/输出激活函数(NIAF/NOAF):去除激活函数,性能大幅下降,说明激活函数对门控机制的非线性表达能力非常重要。
- 全门递归(FGR):增加所有门的递归连接,参数量大幅增加,但性能并未提升,反而可能过拟合。
小结:遗忘门和输出门激活函数对LSTM性能影响最大,是LSTM结构的核心。输入门、peephole等结构可根据实际需求权衡取舍。
该实验表明,LSTM的设计中,遗忘门和非线性激活是保证其强大记忆和建模能力的关键。实际应用中可根据任务复杂度和资源约束,适当简化LSTM结构(如GRU就是一种简化变体)。
特点
优点
- 解决长期依赖问题:
- 通过门控机制控制信息流动
- 避免梯度消失:
- 单元状态提供了梯度传播的捷径
- 更好的记忆能力:
- 可以选择性地记住或忘记信息
缺点
- 结构复杂,参数量大:
- LSTM包含多个门控(遗忘门、输入门、输出门),每个门都需要独立的权重和偏置,导致参数数量远多于普通RNN和GRU。
- 计算开销大,训练速度慢:
- 每个时间步都要计算多个门的激活,前向和反向传播都比GRU和RNN更耗时。
- 难以并行:
- LSTM的每个时间步依赖前一时刻的状态,难以充分利用并行计算资源。
- 依然存在长期依赖问题:
- 虽然LSTM显著缓解了梯度消失,但对于极长序列,长期依赖的捕捉能力仍有限。
- 过拟合风险:
- 参数多,模型复杂,若数据量不足容易过拟合。
门控循环单元GRU
简化结构
GRU是LSTM的简化版本,只包含两个门:
- 重置门:控制历史信息的遗忘程度
- 更新门:控制新信息的更新程度
把input gate和forget gate合成一个reset gate。

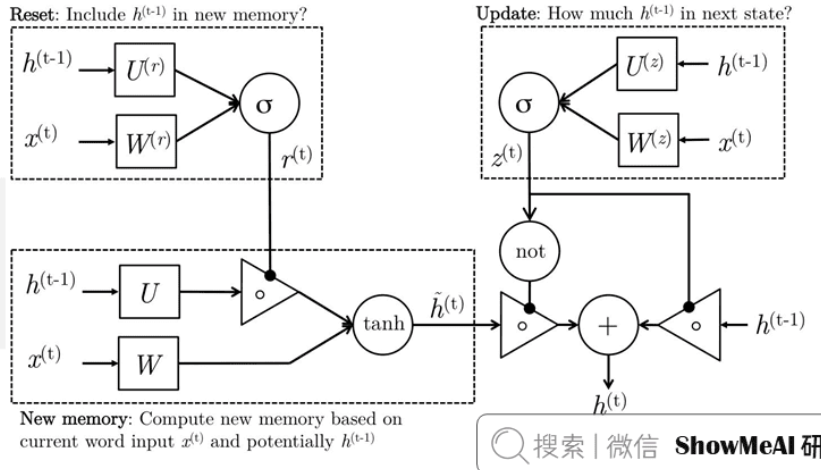
数学表示
更新门:
$$z_t = \sigma(W_z \cdot [h_{t-1}, x_t] + b_z)$$重置门:
$$r_t = \sigma(W_r \cdot [h_{t-1}, x_t] + b_r)$$候选隐藏状态:
$$\tilde{h}_t = tanh(W_h \cdot [r_t \odot h_{t-1}, x_t] + b_h)$$隐藏状态更新:
$$h_t = (1-z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t$$
GRU vs LSTM
| 特性 | LSTM | GRU |
|---|---|---|
| 门控结构 | 3个门(遗忘、输入、输出) | 2个门(重置、更新) |
| 参数量 | 多 | 少 |
| 计算复杂度 | 高 | 低 |
| 表达能力 | 强,理论上更灵活 | 稍弱,但足够大多数任务 |
| 训练速度 | 慢 | 快 |
| 并行能力 | 差 | 略好 |
| 长期依赖建模 | 更强 | 稍弱 |
| 实际表现 | 部分任务略优 | 大多数任务相当,有时更优 |
| 过拟合风险 | 较高 | 较低 |
- 总结:LSTM适合需要强大记忆能力和复杂序列建模的场景,但在大多数实际任务中,GRU以更少的参数和更快的训练速度获得了与LSTM相当甚至更优的效果。需要依据情况选择合适的方法。


