传统生信分析较多使用R语言，本文使用Python。

参考:

Marker基因展示

定义

Marker基因（标记基因）是指在特定细胞类型或细胞状态中特异性高表达的基因。这些基因具有以下特点：

  1. 特异性：在特定细胞类型中显著高表达
  2. 稳定性：表达水平相对稳定
  3. 保守性：在不同样本或条件下保持表达特征

意义

  1. 细胞类型鉴定：帮助识别和定义不同的细胞类型
  2. 细胞状态评估：反映细胞的发育、分化或激活状态
  3. 细胞亚群划分：用于区分细胞亚群
  4. 细胞功能研究：指示细胞的功能特征
  5. 疾病诊断：作为疾病诊断或预后的生物标志物

常见展示方式

在单细胞研究中，常用的Marker基因可视化方法包括：

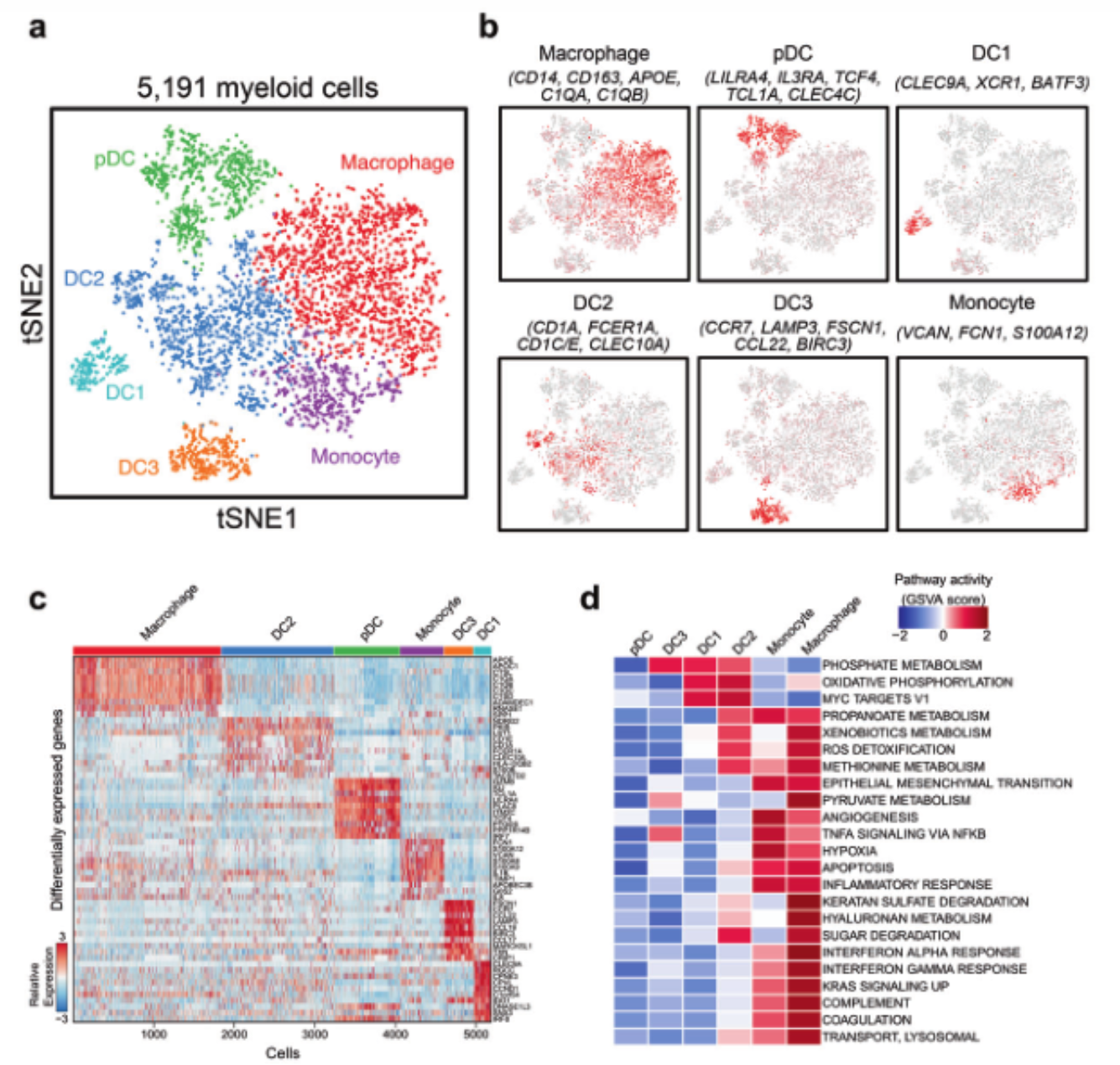
  1. t-SNE/UMAP图：

    • 展示细胞在降维空间中的分布，用颜色表示Marker基因的表达水平
    • 展示单个Marker基因在细胞群中的表达模式
    • 观察基因表达与细胞聚类的关系
    • 发现基因表达的空间分布特征

  2. 热图：

    • 展示多个Marker基因在不同细胞类型中的表达模式
    • 比较不同细胞类型间的基因表达差异
    • 发现基因表达模块和共表达模式

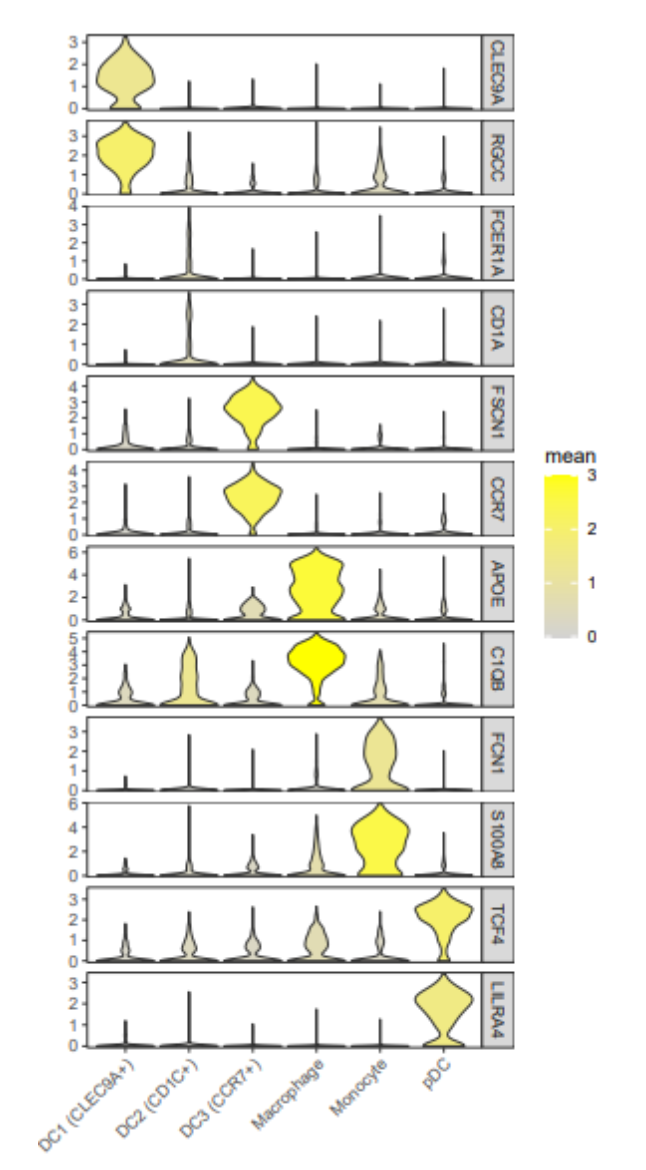
  3. 堆叠小提琴图：

    • 展示Marker基因在不同细胞类型中的表达分布
    • 比较不同细胞类型间的表达水平差异
    • 观察表达量的离散程度和异常值

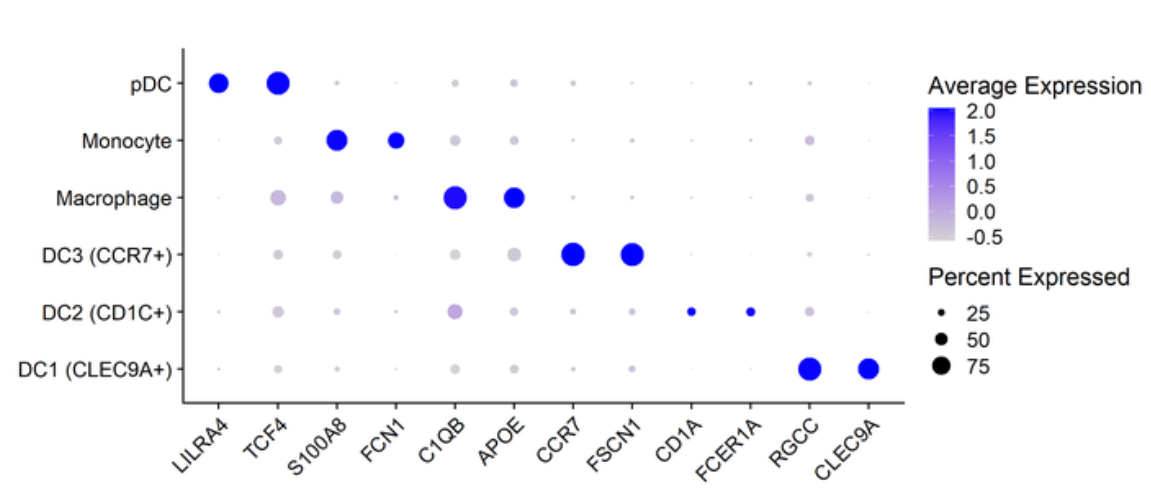
  4. 气泡图：

    • 同时展示Marker基因的表达水平和表达比例
    • 比较多个基因在不同细胞类型中的表达特征
    • 发现细胞类型特异的表达模式

选择合适的可视化方法需要考虑：

  1. 展示的Marker基因数量
  2. 需要展示的信息维度
  3. 数据的复杂程度
  4. 展示的目的和受众

相关概念

  1. 背景基因（Background Genes）：

    • 在所有细胞类型中普遍表达的基因
    • 表达水平相对稳定，不具有细胞类型特异性
    • 通常用于数据标准化和质控

  2. 管家基因（Housekeeping Genes）：

    • 维持细胞基本功能所必需的基因
    • 在不同细胞类型中表达水平相对稳定
    • 常用于实验对照和标准化

  3. 差异表达基因（DEGs）：

    • 在不同条件或细胞类型间表达水平显著差异的基因
    • 可能包括Marker基因，但范围更广
    • 用于发现生物学差异和功能研究
    • 常用：GSEA富集图

ElbowPlot

作用

肘部图用于帮助确定聚类分析中最佳的聚类数，通过绘制不同聚类数下的误差平方和（惯性，Inertia）或轮廓系数等指标，找到使模型性能最佳的聚类数。

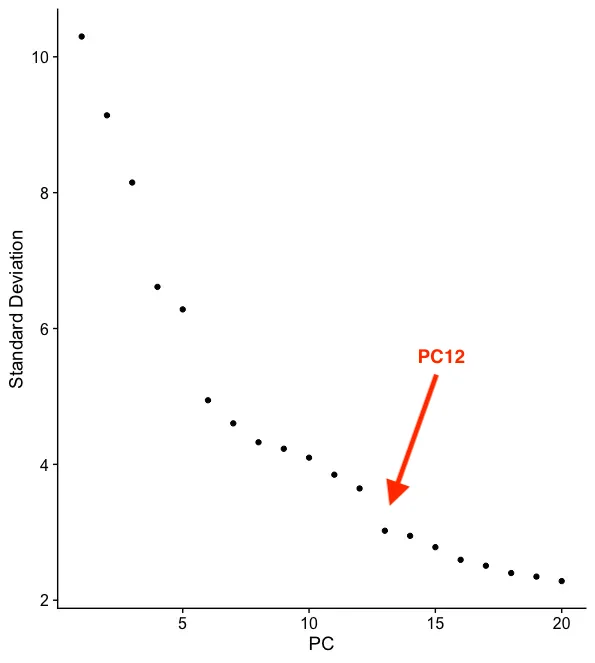
读图

肘部图用于帮助确定主成分分析（PCA）中保留的最佳主成分（PC）数量。通过绘制每个主成分的方差贡献率，可以找到方差贡献率开始显著下降的”肘部”点，该点之后的主成分对方差的贡献较小，可以考虑舍弃。

参数

  • n_clusters：指定聚类的数量，通常是一个整数或整数列表。
  • inertia：误差平方和，表示每个点到其最近的聚类中心的距离的平方和，用于衡量聚类的紧凑性。
  • silhouette_score：轮廓系数，用于评估聚类的分离度和紧致度，取值范围在-1到1之间，值越高表示聚类效果越好。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import matplotlib.pyplot as plt
import numpy as np

# 生成示例数据
np.random.seed(42)
x = np.xxx # PC values from 1 to 20
y = np.yyy # Random standard deviation values

# Sort the y values in descending order for demonstration
y = np.sort(y)[::-1]

# Create the plot
plt.figure(figsize=(8, 6))
plt.scatter(x, y, color='black')

# Annotate PC12 with an arrow and text
plt.annotate('PC12', xy=(12, y[11]), xytext=(15, y[11] + 1),
             arrowprops=dict(facecolor='red', shrink=0.05),
             fontsize=12, color='red')

# Customize the plot
plt.xlabel('PC')
plt.ylabel('Standard Deviation')
plt.title('Elbow Plot Example')
plt.grid(False)

# Display the plot
plt.show()

PCA

作用

PCA 是一种常用的降维技术，能够将高维数据转换为低维表示，同时保留数据中的主要变化趋势。它通过线性变换将数据投影到新的坐标系中，使得新的坐标轴（主成分）按方差大小排序。PCA 在数据可视化、特征提取和噪声过滤等领域有广泛应用。

读图


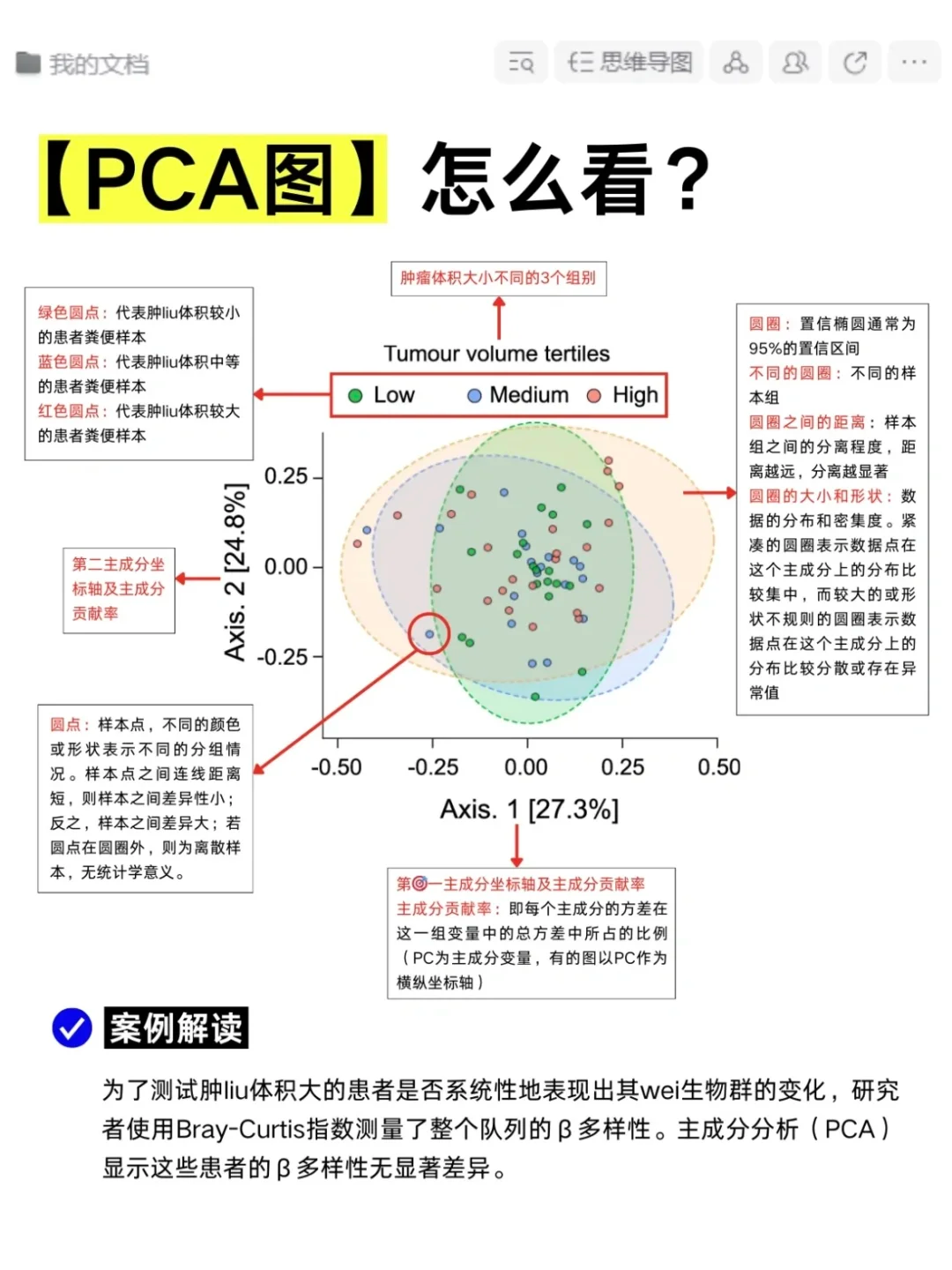
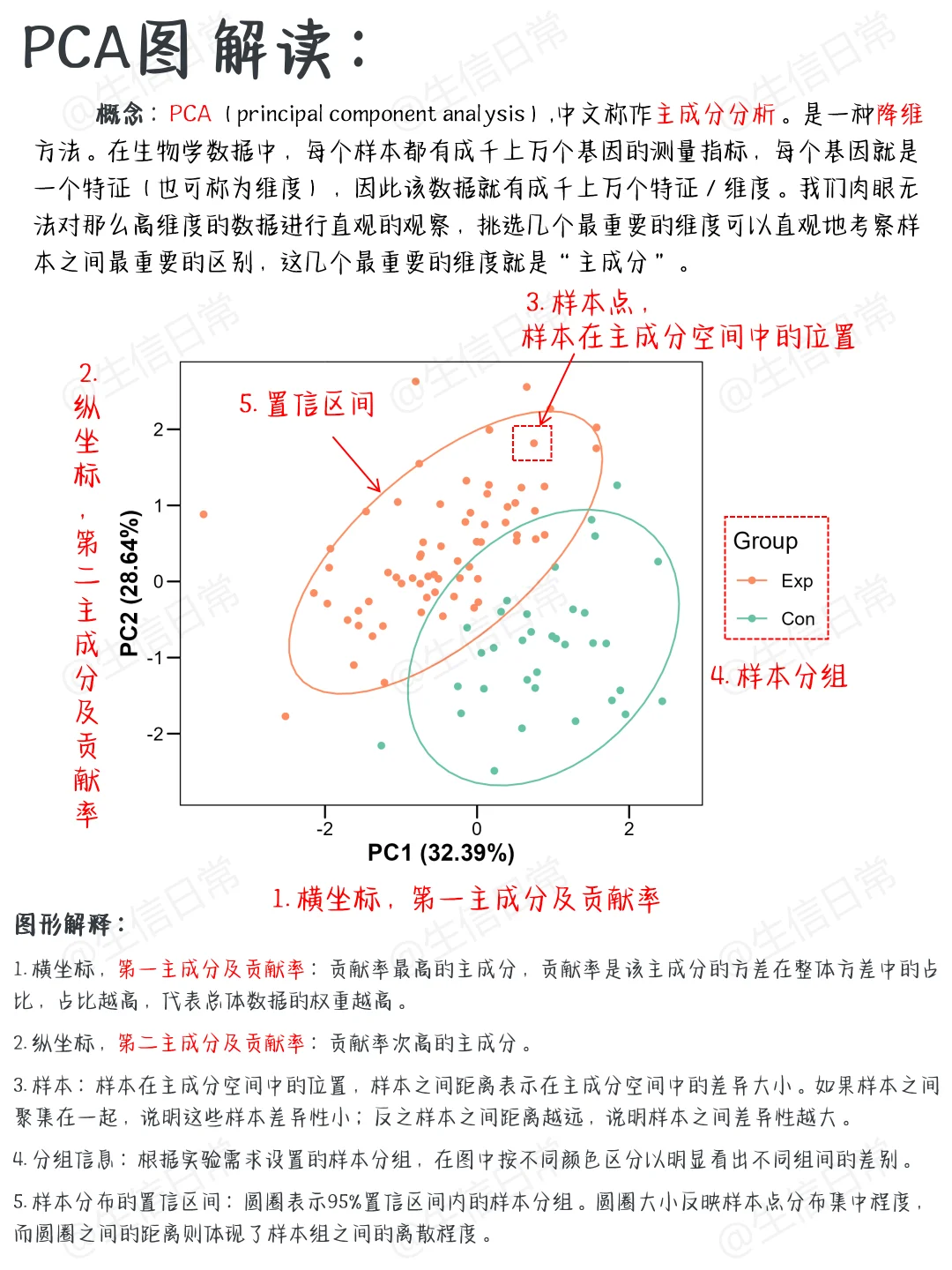
参数

  • n_components：指定要保留的主成分数量，默认为 None，通常根据解释的方差比例或指定的方差阈值来确定，例如保留解释 95% 方差的主成分。
  • whiten：是否对数据进行白化处理，默认为 False，白化处理可以使主成分具有单位方差。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

# 应用 PCA 降维
pca = PCA(n_components=2)
principalComponents = pca.fit_transform(data)

# 绘制 PCA 图
plt.figure(figsize=(8, 6))
plt.scatter(principalComponents[:, 0], principalComponents[:, 1], s=5, cmap='viridis')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA of High-Dimensional Data')
plt.show()

UMAP

作用

UMAP 是一种基于流形学习的降维可视化方法，能将高维的单细胞转录组数据映射到二维或三维空间，便于观察细胞聚类和细胞类型间的连续性，同时保留数据的局部结构。

UMAP 除了在单细胞数据可视化中表现出色外，还广泛应用于其他高维数据的可视化领域，如图像识别、自然语言处理等。

读图

每个点代表一个细胞，不同颜色表示不同的细胞类型或聚类。距离相近的点代表细胞在特征上相似，可能属于同一细胞类型或具有相似的细胞状态。通过观察UMAP图，可以直观地了解细胞群体的结构和分布，发现潜在的细胞亚群和细胞类型间的过渡状态。
UMAP1/UMAP2是聚类的两个维度，一般作为横轴纵轴。

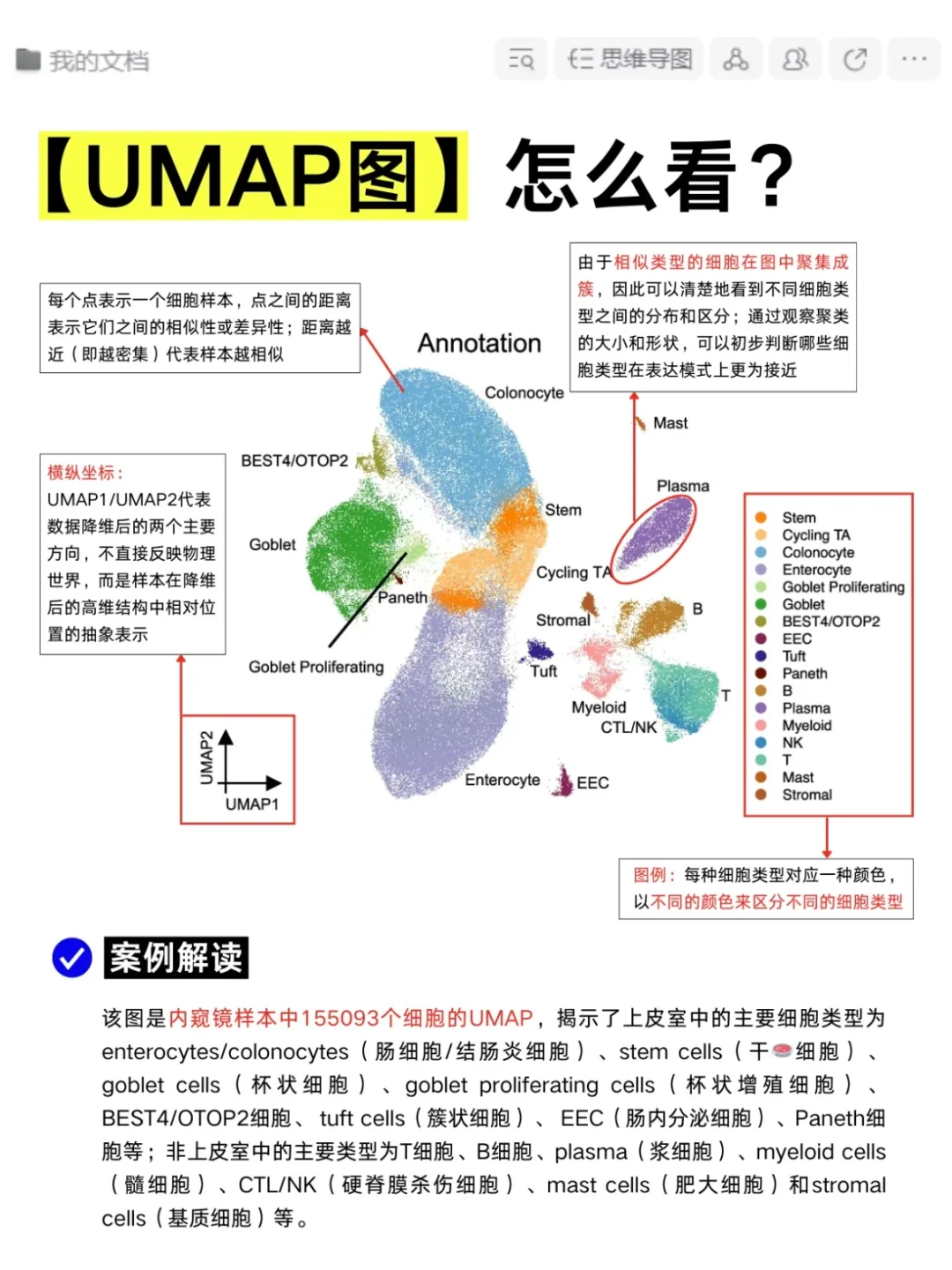
参数

  • n_neighbors，用于指定每个点的邻居个数，较大的值会使embedding更关注全局结构，较小的值则使embedding更关注局部结构
  • min_dist，用于控制嵌入空间中点之间的最小距离，较小的值会使点更紧密地聚集，较大的值会使点更分散
  • metric，用于指定计算距离的度量方式，如’euclidean’、’cosine’等
  • n_components，指定降维后的目标维度，通常为2或3。

示例代码

1
2
3
4
5
6
7
8
9
10
11
# 应用UMAP降维
reducer = umap.UMAP(n_neighbors=15, min_dist=0.1, metric='euclidean', n_components=2)
embedding = reducer.fit_transform(data)

# 绘制UMAP图
plt.figure(figsize=(8, 6))
plt.scatter(embedding[:, 0], embedding[:, 1], s=5, cmap='viridis')
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.title('UMAP of Single Cell Data')
plt.show()

t-SNE

作用

t-SNE 是一种常用的非线性降维可视化技术，能够揭示数据的局部结构，并在降维过程中尽可能地保留数据的相似性，常用于单细胞数据中细胞类型或聚类的可视化。

t-SNE的降维关键：把高纬度的数据点之间的距离转化为高斯分布概率。高纬度相似度用高斯，低纬度用t分布，然后设置一个惩罚函数(KL散度)，就实现了x降低维度但是保留一定局部特征的方法。降维必然带来信息损失，TSNE保留局部信息必然牺牲全局信息，而因为t分布比高斯分布更加长尾，可以一定程度减少这种损失。

t-SNE 在图像识别、文本分类等领域也有广泛应用，用于数据的可视化和探索性分析。

读图

图中每个点代表一个细胞，颜色可表示不同的细胞类型、聚类或其他特征。t-SNE 会将相似的细胞聚集在一起，不同的簇可能代表不同的细胞类型或状态。需要注意的是，t-SNE 的结果可能因参数设置和随机性而存在一定的变化。

参数

  • n_components，目标嵌入空间维度，通常为2。
  • perplexity，困惑度参数，较大的困惑度会使邻居的数量更大，更适合发现全局结构，较小的困惑度则更关注局部结构。默认为30，建议取值在5到50之间。
  • early_exaggeration，早期夸大因子，影响初始阶段数据的聚集程度。表示嵌入空间簇间距的大小，默认为12，该值越大，可视化后的簇间距越大。
  • learning_rate，学习率，影响优化过程的步长，过小会导致收敛慢，过大可能导致不收敛；表示梯度下降的快慢，默认为200，建议取值在10到1000之间。
  • n_iter，最大迭代次数。默认为1000，自定义设置时应保证大于250。
  • min_grad_norm, 如果梯度小于该值，则停止优化。默认为1e-7。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
import numpy as np

# 应用 t-SNE 降维
tsne = TSNE(n_components=2, perplexity=30, early_exaggeration=12, learning_rate=200, n_iter=1000)
embedding = tsne.fit_transform(data)

# 绘制 t-SNE 图
plt.figure(figsize=(8, 6))
plt.scatter(embedding[:, 0], embedding[:, 1], s=5, cmap='viridis')
plt.xlabel('t-SNE 1')
plt.ylabel('t-SNE 2')
plt.title('t-SNE of Single Cell Data')
plt.show()

对比三种降维聚类

好的，以下是 t-SNE、UMAP 和 PCA 三种降维技术的详细对比表格，涵盖了核心思想、数学基础、关键特性、优缺点和适用场景等方面：

t-SNE vs UMAP vs PCA 详细对比表

特性/维度 PCA (主成分分析) t-SNE (t-分布随机邻域嵌入) UMAP (一致流形逼近与投影)
核心思想 最大化投影方差，找到正交的主方向。 保持局部邻域结构，最小化高低维概率分布(KL散度)。 保持局部邻域结构，并尝试保留全局结构(模糊拓扑)。
数学基础 线性代数 (特征值分解/SVD)。 概率论、信息论 (KL散度) + 梯度下降。 拓扑学 (单纯复形)、黎曼几何 + 优化 (随机梯度下降)。
线性/非线性 严格线性。 强非线性。 强非线性。
结构保持重点 全局结构 (方差/欧氏距离，尤其是远距离点)。 极度强调局部结构 (邻近点关系)。弱化全局结构。 平衡局部与全局结构 (局部更优先)。
距离度量保持 试图保持全局欧氏距离 (线性映射)。 不直接保持距离，保持局部邻域概率关系。 不直接保持距离，保持局部连通性/拓扑关系。
可解释性 高。主成分是原始特征的线性组合，可赋予意义。 低。低维坐标轴通常无直接解释意义。 低。低维坐标轴通常无直接解释意义。
计算效率 非常高 (O(min(n³, d³))， SVD优化后高效)。 较低 (O(n²)， Barnes-Hut优化后O(n log n))。 较高 (理论O(n^{1.14})， 通常比t-SNE快)。
确定性 确定性。给定数据和维度，结果唯一(符号除外)。 随机性。结果依赖于随机初始化和优化过程。 随机性。结果依赖于随机初始化和优化过程。
关键参数 目标维度 (通常无其他关键参数)。 困惑度(Perplexity) (控制邻域大小， 影响簇大小)。 邻近邻居数(n_neighbors) (控制局部/全局平衡)。
参数敏感性 低。 高。Perplexity对结果形态影响很大。 中。n_neighbors有影响，但相对t-SNE鲁棒性稍好。
异常值鲁棒性 较低 (基于方差， 易受大值影响)。 中 (概率方法提供一定鲁棒性)。 中高 (基于连通性， 对异常点相对不敏感)。
拥挤问题 无此问题 (线性投影)。 有 (使用t分布尾部缓解)。 设计上规避 (基于黎曼几何距离)。
可视化特性 清晰展示主要变化方向和全局分布。簇分离可能模糊。 簇内紧凑、簇间分离极佳，利于揭示局部聚类结构。 簇结构清晰，局部紧凑且全局相对关系更合理。
主要优点 快、简单、可解释、保全局结构、去线性噪声。 揭示复杂非线性局部结构、聚类可视化效果极佳。 速度快、平衡局部与全局、可视化效果好、可扩展性强。
主要缺点 无法捕捉非线性结构、对异常值敏感、局部结构模糊。 慢、随机性、不保全局结构、参数敏感、结果难解释。 随机性、理论基础相对复杂(对用户)、结果难解释。
典型应用场景 数据预处理、特征提取、去噪、探索线性相关、初步可视化。 探索性数据分析(聚类结构)、高维数据可视化(聚焦局部)。 探索性数据分析(平衡视角)、高维数据可视化、大规模数据降维。

重要说明与注意事项：

  1. 全局 vs 局部： 这是核心区别。
    • PCA：强全局，弱局部。
    • t-SNE：强局部，弱全局（甚至可能扭曲）。
    • UMAP：力求在局部优先的前提下，更好地保留全局结构（如簇间相对位置、大小）。
  2. 可视化目的：
    • 想看主要变化趋势和总体分布？ -> PCA。
    • 想看清密集的局部聚类和簇结构？ -> t-SNE (尤其当簇很多且复杂时)。
    • 想平衡地看局部聚类和整体布局，且需要速度？ -> UMAP (当前最常用的可视化选择之一)。
  3. 距离解释： 切勿直接比较 t-SNE 或 UMAP 图中不同簇之间的距离！这些距离在数学上没有可靠的全局意义。只有同一个簇内的点距离较近表示它们在高维空间也相似。
  4. 参数调整： t-SNE (perplexity) 和 UMAP (n_neighbors) 的参数对结果影响显著。需要根据数据集大小和期望的”尺度”（想看多细的局部结构）进行调整。PCA 通常只需指定目标维度。
  5. 多次运行： 由于 t-SNE 和 UMAP 的随机性，对同一数据集运行多次，得到的低维嵌入在旋转、镜像、微小位置偏移上可能不同，但拓扑结构（如哪些点聚集在一起）应保持稳定。如果结构变化很大，可能需要调整参数或检查数据。
  6. 可扩展性： UMAP 在处理非常大的数据集（数十万甚至百万级样本）时通常比 t-SNE 更具优势，速度更快且内存消耗更低。

总结选择建议：

  • 首选探索性可视化 (现代实践)： UMAP (速度、效果、局部/全局平衡的综合优势)。
  • 深入聚焦局部聚类结构： t-SNE (可能揭示更精细的局部模式)。
  • 理解主要变化方向、预处理、去噪、可解释性： PCA (经典、高效、可靠)。
  • 大规模数据降维： UMAP 或 PCA (取决于是否需要非线性)。

热图

作用

热图可以展示基因在不同细胞或细胞聚类中的表达水平，有助于识别差异表达基因和细胞类型的特异性基因。
热图在基因表达分析、蛋白质组学等领域也有广泛应用，用于展示数据的表达模式和聚类关系。

读图

热图的行通常代表基因，列代表细胞或细胞聚类。颜色的深浅表示基因表达水平的高低，通常使用颜色条来指示表达水平的数值范围。通过观察热图，可以直观地看到哪些基因在特定的细胞或聚类中高表达或低表达。


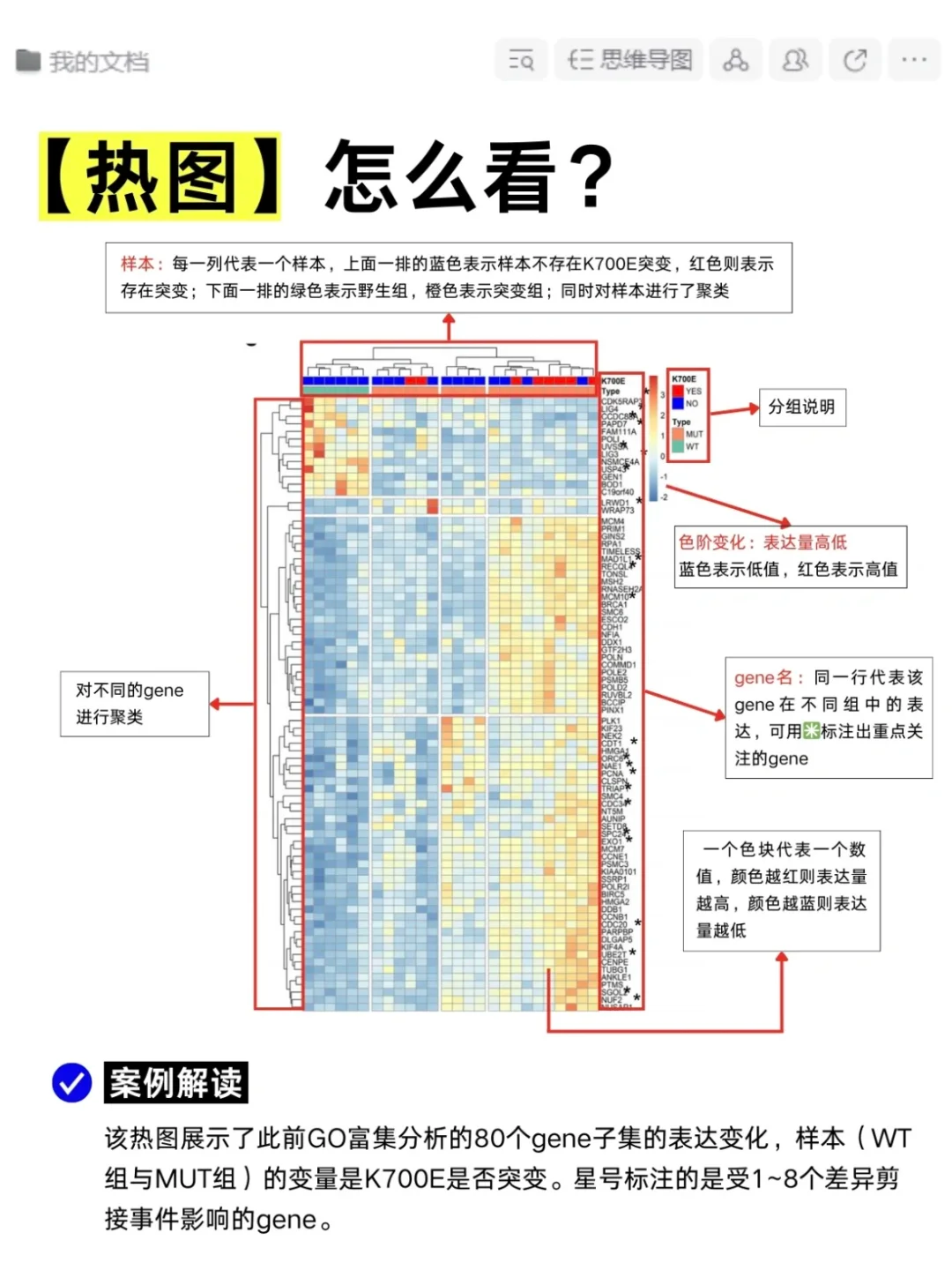
参数

  • data，输入数据，通常是基因表达矩阵
  • row_cluster，是否对行进行聚类
  • col_cluster，是否对列进行聚类
  • cmap，颜色映射，如'viridis'、'hot'等
  • figsize，图的大小
  • xticklabels，是否显示 x 轴刻度标签
  • yticklabels，是否显示 y 轴刻度标签。

示例代码

1
2
3
4
5
6
7
8
9
10
11
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np

# 绘制热图
plt.figure(figsize=(12, 8))
sns.heatmap(data, xticklabels=False, yticklabels=True, cmap='viridis')
plt.xlabel('Cells')
plt.ylabel('Genes')
plt.title('Heatmap of Gene Expression')
plt.show()

气泡图

作用

气泡图是一种多维度数据可视化方法，通过气泡的大小、颜色和位置来展示多个变量的信息。在单细胞分析中，气泡图常用于展示基因在不同细胞类型中的表达情况，其中气泡的大小表示基因表达水平，颜色可以表示不同的细胞类型或表达模式。

特点

优点

  1. 多维度展示：可以同时展示多个维度的信息（位置、大小、颜色）
  2. 直观性：通过气泡大小直观地展示表达量的差异
  3. 信息密度：在有限的空间内展示大量信息
  4. 比较能力：便于比较不同基因在不同细胞类型中的表达模式
  5. 美观性：视觉效果吸引人，适合用于展示和报告

缺点

  1. 数据量限制：当数据点过多时可能显得拥挤
  2. 精确度：难以精确读取具体的表达值
  3. 气泡重叠：当气泡较多时可能出现重叠，影响可读性
  4. 比例尺：需要合理设置气泡大小的比例尺，避免误导
  5. 图例复杂性：多维度信息可能导致图例复杂

应用场景

  1. 基因表达分析：展示多个基因在不同细胞类型中的表达情况
  2. 细胞类型比较：比较不同细胞类型中基因表达的特征
  3. 差异表达基因展示：突出显示差异表达的基因
  4. 细胞状态转换：展示细胞状态转换过程中的基因表达变化
  5. 通路分析：展示特定通路中基因的表达模式

读图

气泡图中：

  • 气泡的位置表示基因和细胞类型的关系
  • 气泡的大小反映基因表达水平，气泡越大表示表达量越高
  • 气泡的颜色可以表示不同的表达模式或细胞类型
  • 通过观察气泡的分布模式，可以识别特定基因在不同细胞类型中的表达特征

参数

  • x：x轴变量，通常是细胞类型或聚类
  • y：y轴变量，通常是基因名称
  • size：气泡大小，通常表示基因表达水平
  • color：气泡颜色，可用于区分不同的表达模式或细胞类型
  • alpha：透明度，控制气泡的透明度
  • scale：气泡大小的缩放比例
  • palette：颜色映射方案

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd

# 创建示例数据
data = pd.DataFrame({
    'Cell_Type': ['Type1', 'Type2', 'Type3'] * 3,
    'Gene': ['Gene1', 'Gene2', 'Gene3'] * 3,
    'Expression': [0.8, 0.5, 0.3, 0.6, 0.7, 0.4, 0.2, 0.9, 0.1]
})

# 绘制气泡图
plt.figure(figsize=(10, 6))
sns.scatterplot(data=data, x='Cell_Type', y='Gene', 
                size='Expression', hue='Expression',
                sizes=(100, 1000), palette='viridis')
plt.title('Bubble Plot of Gene Expression')
plt.xlabel('Cell Type')
plt.ylabel('Gene')
plt.legend(title='Expression Level', bbox_to_anchor=(1.05, 1), loc='upper left')
plt.tight_layout()
plt.show()

小提琴图

作用

小提琴图（Violin Plot）是一种结合了箱线图和核密度图特点的数据可视化图表，用于展示数据的分布情况。可以展示基因表达的分布特征.包括中位数、四分位数范围、分布形状等。

小提琴图在基因表达分析、生物统计等领域有广泛应用，用于展示数据的分布特征和统计信息。

  • 数据分布比较/多变量分析：通过观察小提琴图的形状、宽度和长度，比较不同组别或类别的数据分布，直观了解数据密度和范围，发现其中的差异性和相似性。
  • 异常值检测：快速识别数据集中的异常值或离群点，为后续分析处理提供指导。
  • 探索因素影响：研究一个因素对另一个因素的影响。按一个因素分组，观察另一个因素的小提琴图，了解两者之间的关系和影响。
  • 时间序列分析：适用于观察随时间变化的数据分布。通过比较不同时间点的数据分布，识别趋势和模式。

读图

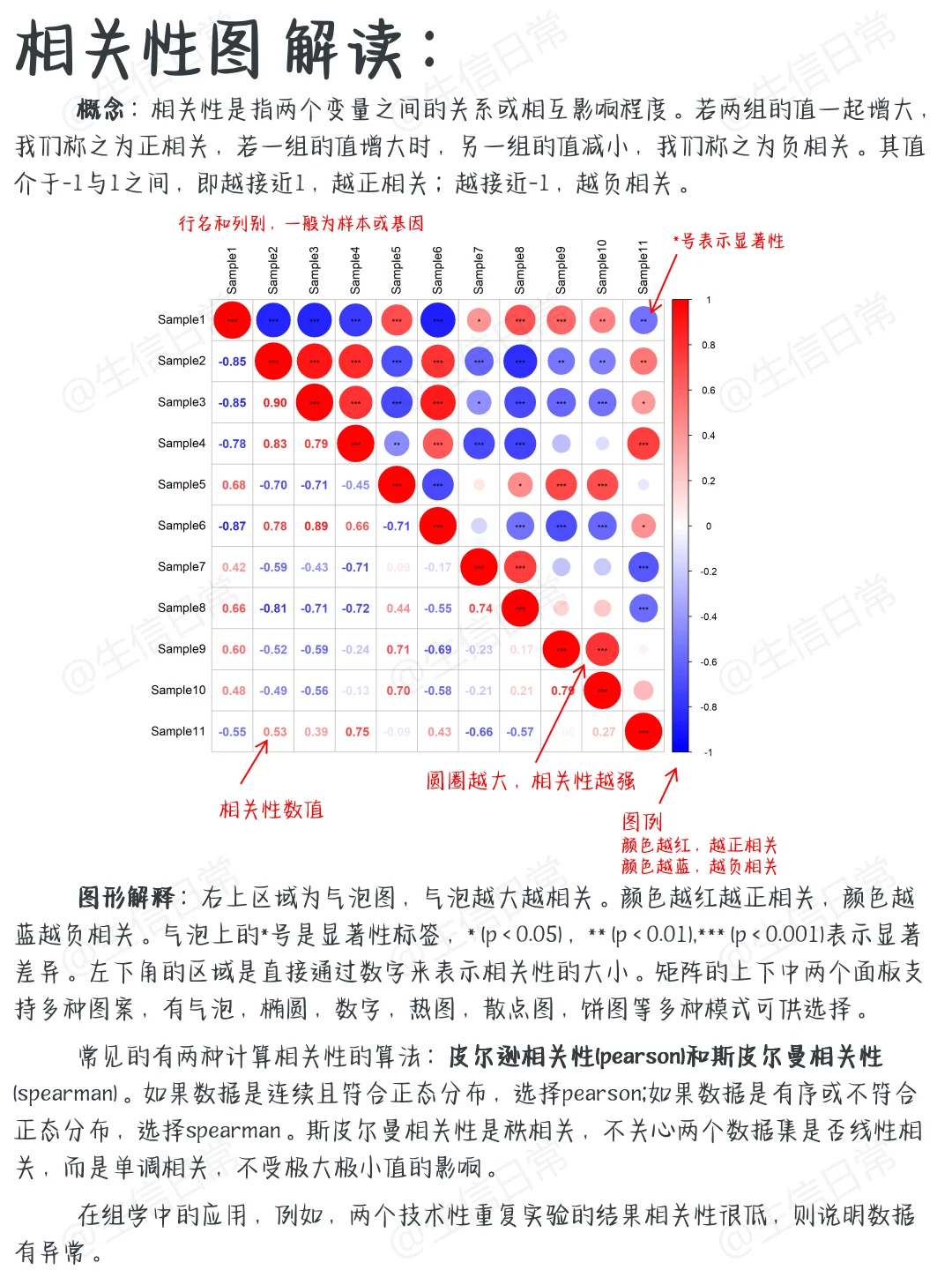
小提琴图的宽度表示基因表达的密度，较宽的部分表示在该表达水平的细胞数量较多。内部的箱线图显示了数据的中位数、四分位数范围和异常值等统计信息。通过比较不同组间的小提琴图，可以了解基因在不同细胞类型或条件下的表达分布差异。


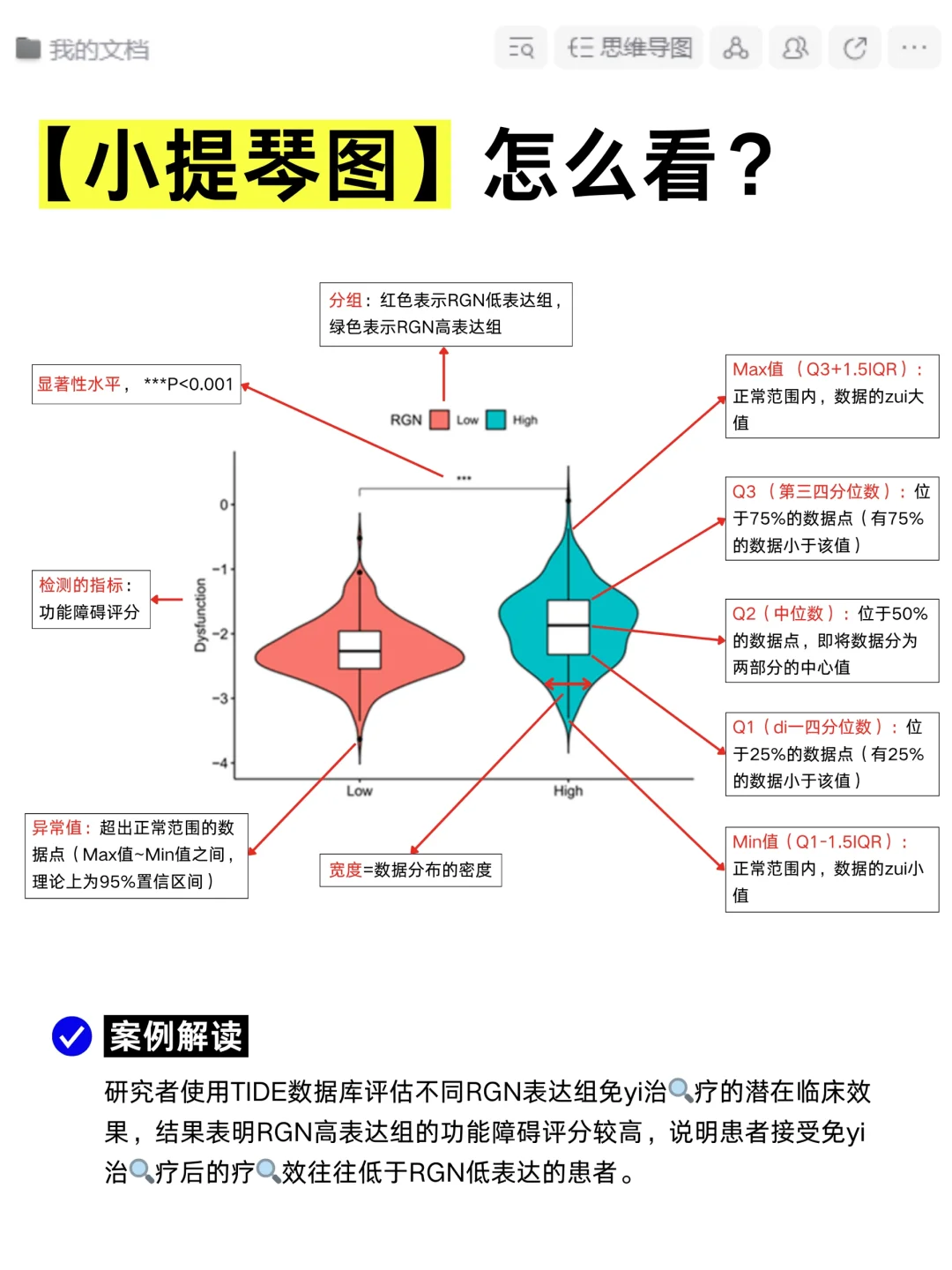
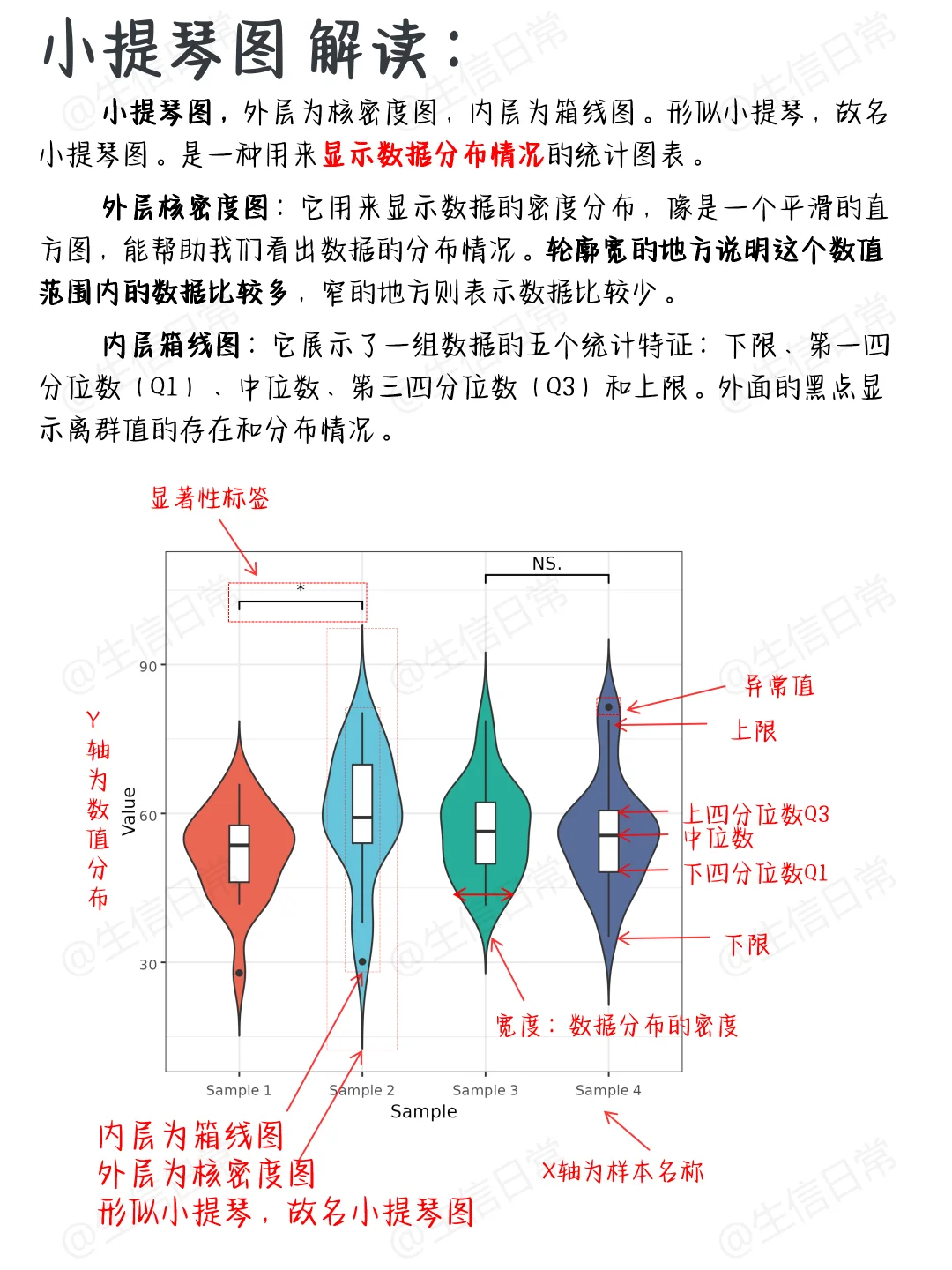
参数

  • x，分组变量，通常是细胞类型或聚类
  • y，数值变量，如基因表达水平
  • data，输入数据框
  • inner，指定内部箱线图的类型，如'box'、'quartile'等
  • bw，带宽参数，影响核密度估计的平滑程度
  • cut，控制密度曲线在数据范围外的延伸程度
  • scale，控制小提琴图的宽度比例。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np

# 绘制小提琴图
plt.figure(figsize=(10, 6))
sns.violinplot(x='Cell_Type', y='Gene_1', data=data, inner='quartile', palette='Set2')
plt.xlabel('Cell Type')
plt.ylabel('Gene Expression')
plt.title('Violin Plot of Gene Expression')
plt.show()

等高线图

作用

等高线图可以展示基因表达密度或某些特征在二维空间中的分布情况，有助于识别高密度区域和基因表达的空间模式。
等高线图在地理信息系统、气象学等领域有广泛应用，用于展示地理数据、气象数据等的分布情况。

读图

等高线连接的是具有相同特征值的点，线条越密集表示该区域的变化越快。颜色的深浅结合等高线可以更直观地反映特征值的高低和分布趋势。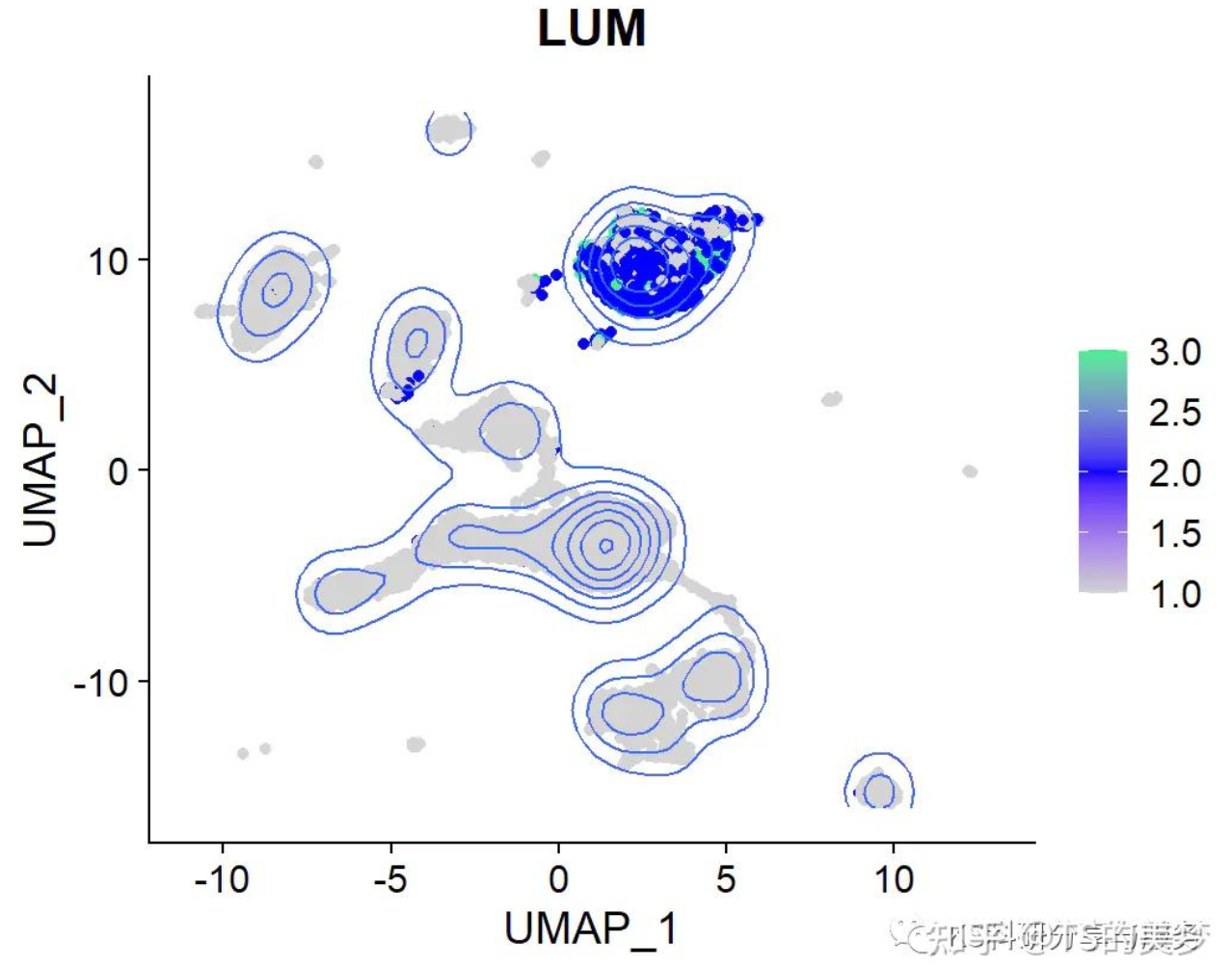


参数

  • x 和y，通常是降维后的坐标，如 UMAP 或 t-SNE 的第一、二个主成分；
  • z，表示基因表达水平或其他特征值
  • levels，指定等高线的数量或具体数值
  • cmap，颜色映射
  • extend，控制等高线图的扩展方式，如'neither'、'both'等
  • alpha，透明度。

示例代码

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import matplotlib.pyplot as plt

# 绘制等高线图
plt.figure(figsize=(8, 6))
contour = plt.contourf(X, Y, Z, levels=20, cmap='viridis', alpha=0.8)
plt.colorbar(contour)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Contour Plot')
plt.show()

密度图/核密图

作用

密度图通过核密度估计展示基因表达或细胞分布的密度，能够突出高密度区域，帮助识别细胞聚集的位置和模式。
密度图在统计学、概率论等领域有广泛应用，用于展示数据的概率密度分布。

读图

密度图中曲线的峰值位置表示数据的高密度区域，曲线的形状反映了数据的分布特征。颜色或阴影的深浅可表示密度的高低。
密度图：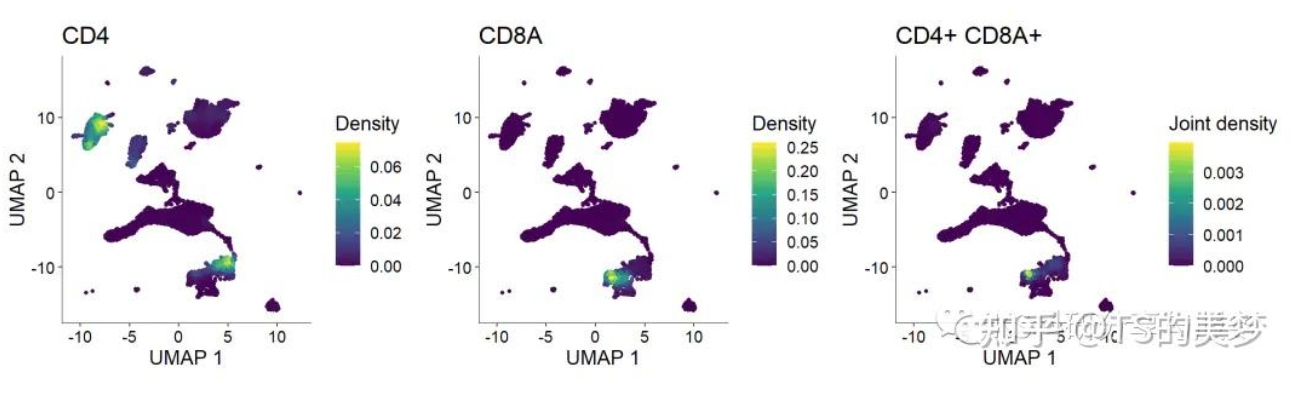

核密图：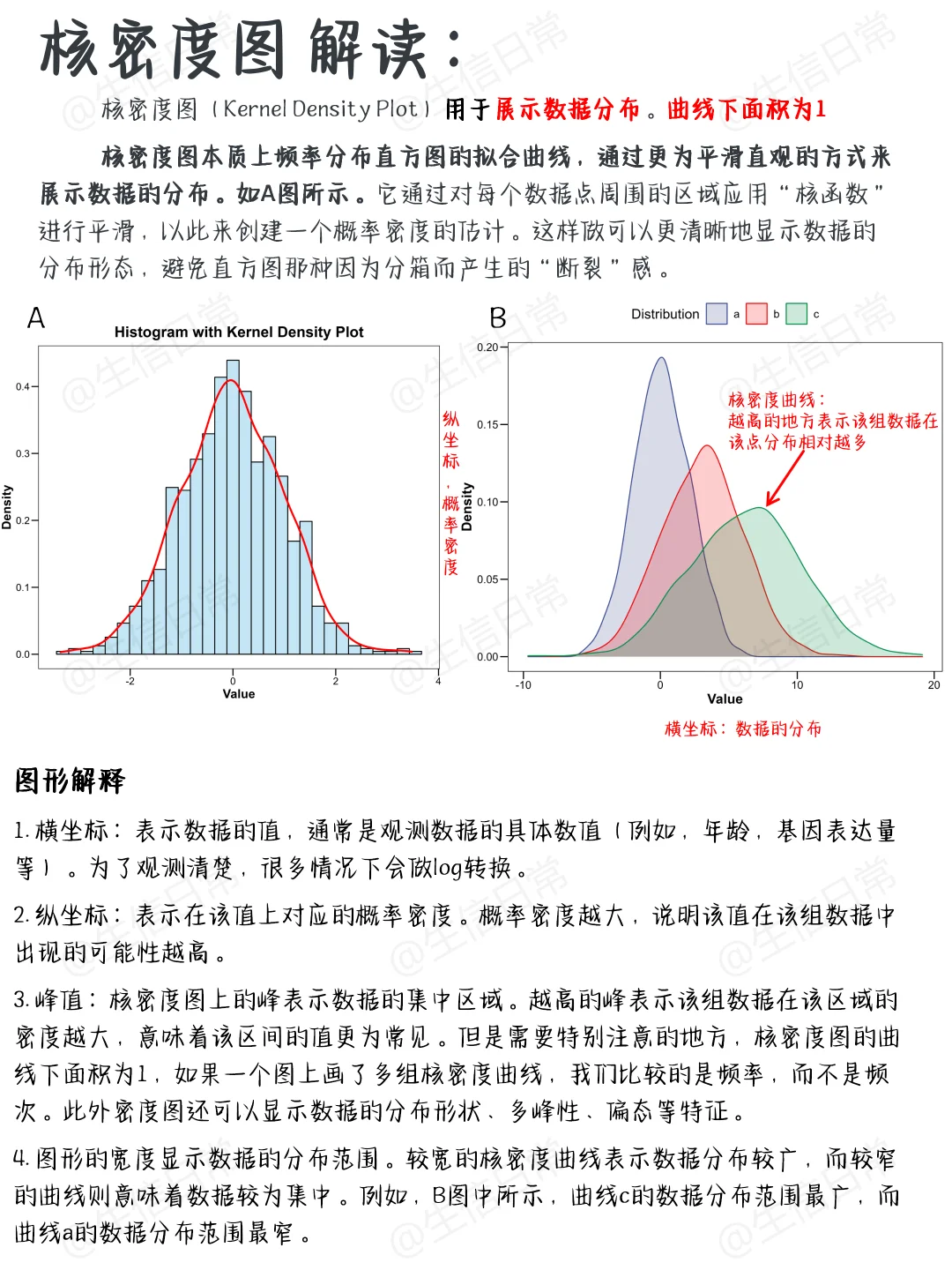


参数

  • values，输入数据，如基因表达值
  • bw_method，带宽计算方法，可指定为'scott'、'silverman'或一个标量
  • ind，指定用于计算密度的网格点
  • kernel，核函数类型，如'gaussian'、'tophat'等
  • weights，可为数据点指定权重。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np

# 绘制密度图
plt.figure(figsize=(8, 6))
sns.kdeplot(data, shade=True, color='blue')
plt.xlabel('Values')
plt.ylabel('Density')
plt.title('Density Plot')
plt.show()

火山图

作用

火山图用于展示基因表达的差异分析结果，横轴表示基因表达的对数值变化倍数，纵轴表示统计显著性（如 p 值的对数值），能够直观地识别差异表达基因。
火山图在基因表达分析、蛋白质组学等领域有广泛应用，用于展示差异分析结果。

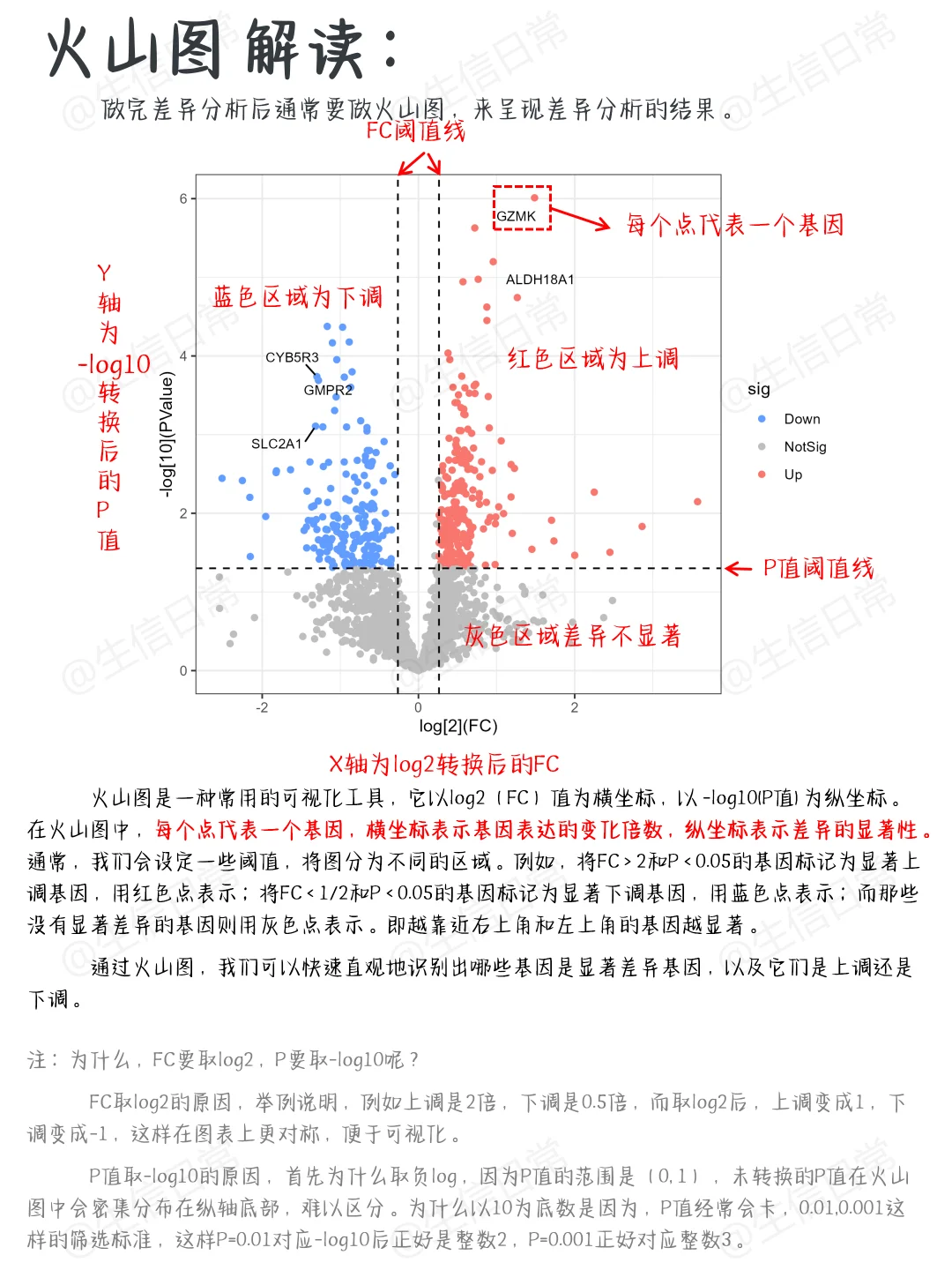
读图

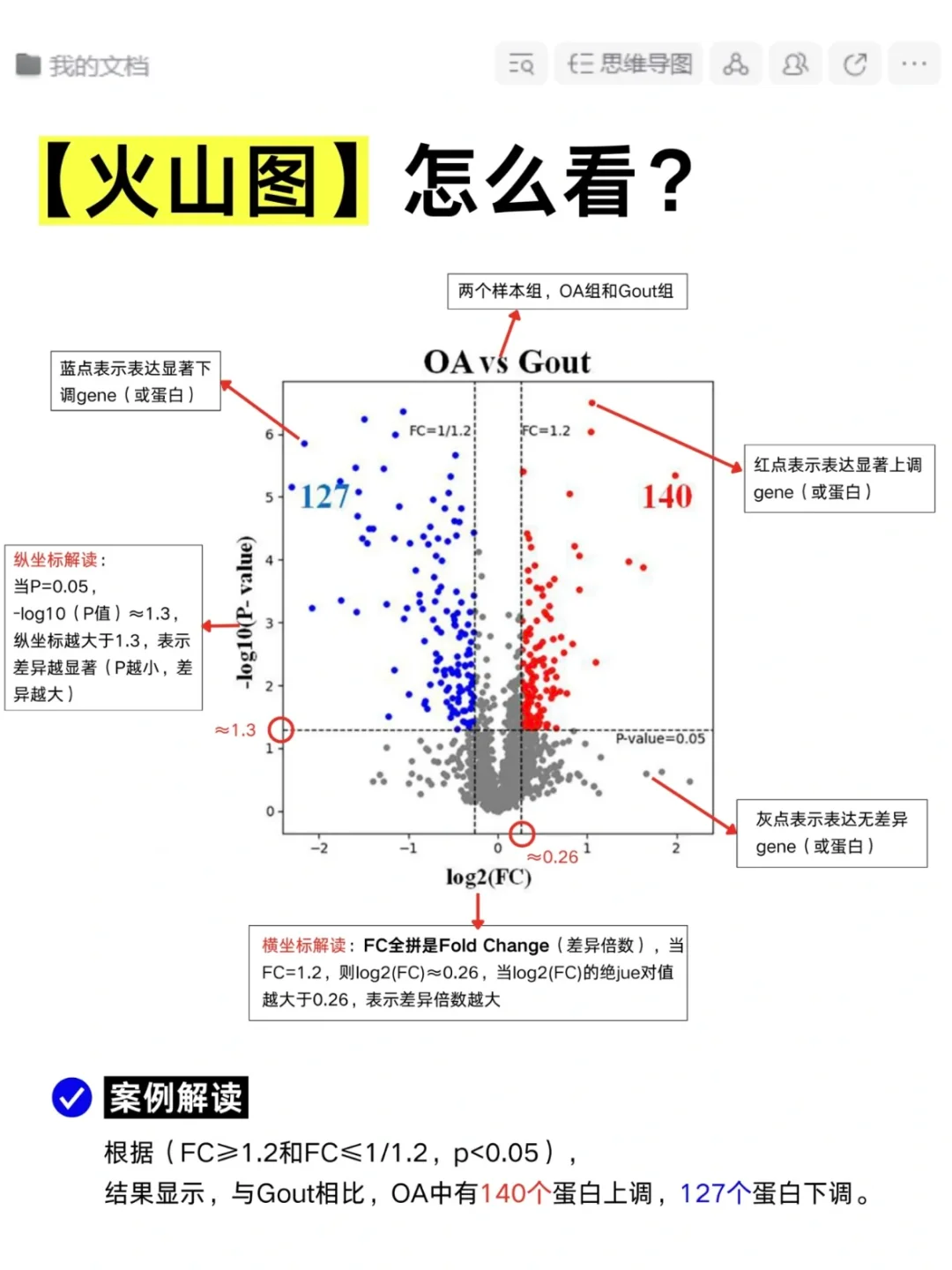
火山图中，横轴表示基因表达的变化倍数，纵轴表示统计显著性。通常，红色点表示上调的差异表达基因，蓝色点表示下调的差异表达基因，灰色点表示非差异表达基因。

  • 上调 ：通常指基因在实验组或特定条件下表达水平高于对照组或基准条件。红色点表示上调的差异表达基因，意味着这些基因在研究的特定条件下表达量增加。
  • 下调 ：通常指基因在实验组或特定条件下表达水平低于对照组或基准条件。蓝色点表示下调的差异表达基因，意味着这些基因在研究的特定条件下表达量减少。

参数

  • logfc，基因表达的对数值变化倍数
  • pval，统计显著性 p 值
  • alpha，显著性阈值
  • is_log2，是否使用 log2 转换。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

# 绘制火山图
plt.figure(figsize=(10, 8))
sns.scatterplot(x='logfc', y='pval', data=data, palette='coolwarm', alpha=0.6)
plt.axhline(y=-np.log10(0.05), color='red', linestyle='--')
plt.axvline(x=1, color='red', linestyle='--')
plt.axvline(x=-1, color='red', linestyle='--')
plt.xlabel('log2(Fold Change)')
plt.ylabel('-log10(p-value)')
plt.title('Volcano Plot')
plt.show()

山脊图

作用

山脊图用于展示多个组之间的分布情况，每个组的分布以密度曲线的形式呈现，可以直观地比较不同组的分布特征，同时保持分布的整体形状。

读图

每个密度曲线代表一个组的分布情况，曲线的形状和位置反映了组内数据的分布特征。通过比较不同组的密度曲线，可以了解组间的分布差异。
山脊图在生物统计、社会科学等领域有广泛应用，用于展示多组分布的比较。

特点

优点

①比较能力:山脊图非常适合比较不同分布的形状和大小，清晰地展示不同组之间的变化和趋势。
②空间效率:通过在单个图中堆叠密度曲线，山脊图有效地利用空间，显示多组数据，避免了创建多个单独的密度图。
③美观性:山脊图在视觉上吸引人，可以用不同的颜色和样式来区分不同的组，使得数据更加生动和直观。
④趋势识别:可以轻松识别多个群体数据中的共同模式和异常值⑤数据量:适用于展示大量数据集，而不会显得拥挤或不清晰。

缺点

①过度拥挤:如果组的数量过多，山脊图可能会显得拥挤，使得个别分布难以辨认。
②精que度:由于重叠，难以精que读取特定点的值，尤其是在分布之间的重
叠区域。
③数值比较:虽然能够展示分布趋势，但不适合精que比较不同组之间的数
值。
④边缘效应:在堆叠的密度图中，可能会产生误导，例如，边缘的分布可能
看起来比实际更少。

参数

  • data，输入数据
  • hue，分组变量
  • palette，颜色映射
  • bw_method，带宽计算方法
  • common_norm，是否对所有组使用相同的标准化。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns


# 绘制山脊图
plt.figure(figsize=(10, 6))
sns.kdeplot(data=data, x='Value', hue='Group', palette='Set2', fill=True, common_norm=False)
plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Ridgeline Plot')
plt.show()

比较密度图与山脊图

  • 密度图:揭示分布的精髓。密度图是一个二维图，它描绘了数据在特定范围内分布的情况，主要通过堆叠垂直线来构建，形成一条平滑的曲线，代表数据的概率密度函数。

  • 山脊图:揭示数据的隐藏层次。山脊图是对密度图的扩展，它不仅展示了数据的分布，还揭示了数据分组或类别之间的差异，主要通过并排放置多个密度曲线来构建，每个曲线代表一个不同的组或类别。
    两者的区别

  • 维度:密度图是二维图，而山脊图是三维图。

  • 分组:密度图不显示分组信息，而山脊图则显示。

  • 比较:密度图专注于单个分布，而山脊图允许比较多个分布。。

  • 适用性:密度图适用于连续数据，而山脊图适用于连续数据和分组数据。


和弦图

作用

和弦图用于展示细胞类型之间的相互关系、转换关系或基因共表达关系等，能够直观地呈现不同元素之间的联系强度和模式。
和弦图在社交网络分析、生态学等领域有广泛应用，用于展示元素之间的关系和交互。

参数

  • matrix，输入矩阵，表示元素之间的关系强度
  • labels，元素的标签
  • colormap，颜色映射
  • width，控制弧的宽度
  • pad，控制弧之间的间距
  • chordwidth，控制和弦的宽度。

读图

和弦图由弧和连接弧的和弦组成，弧的长度表示元素自身的值，和弦的粗细表示元素之间关系的强度。颜色可用于区分不同的元素或关系类型。


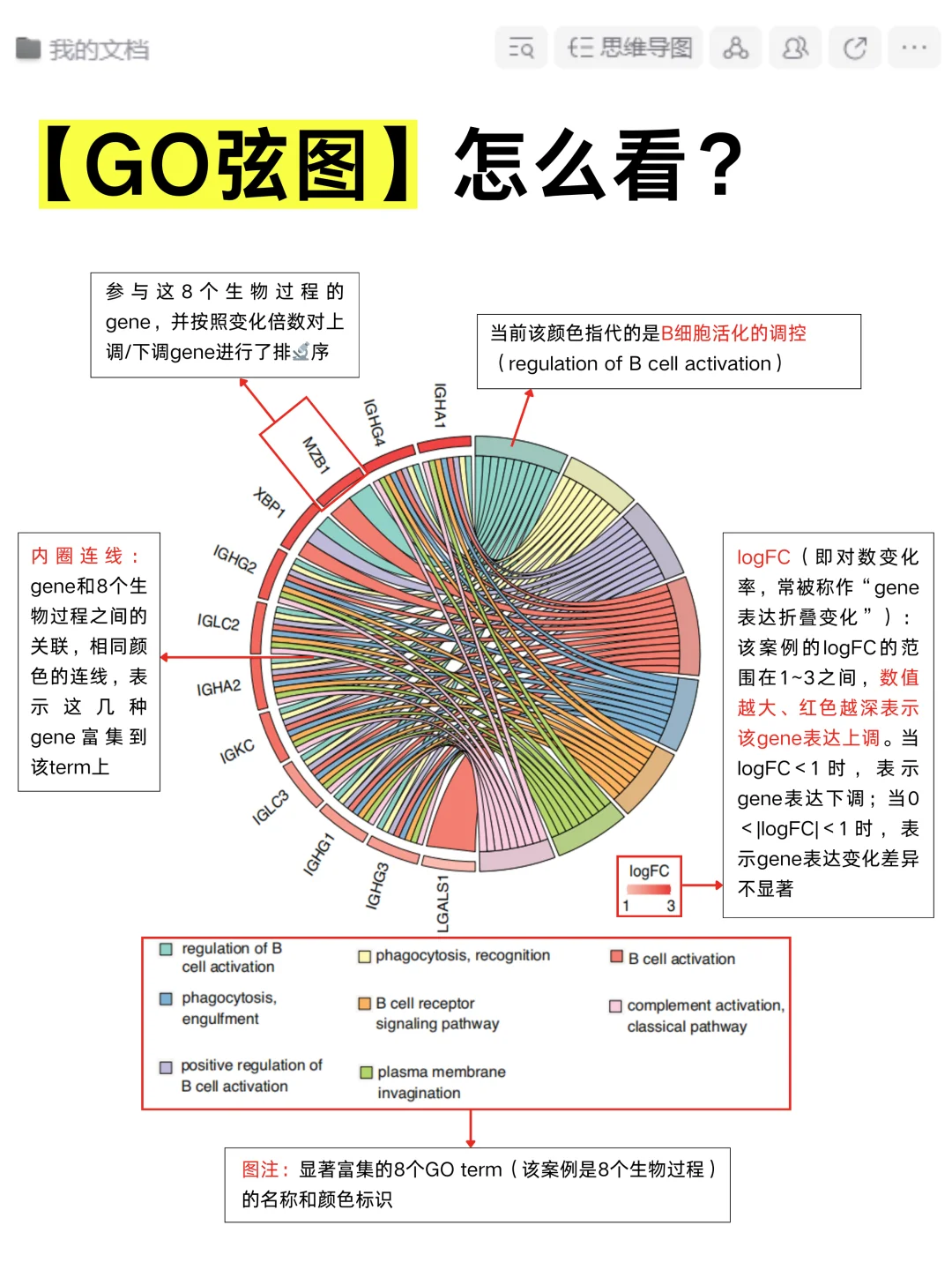
国家合作和弦图：

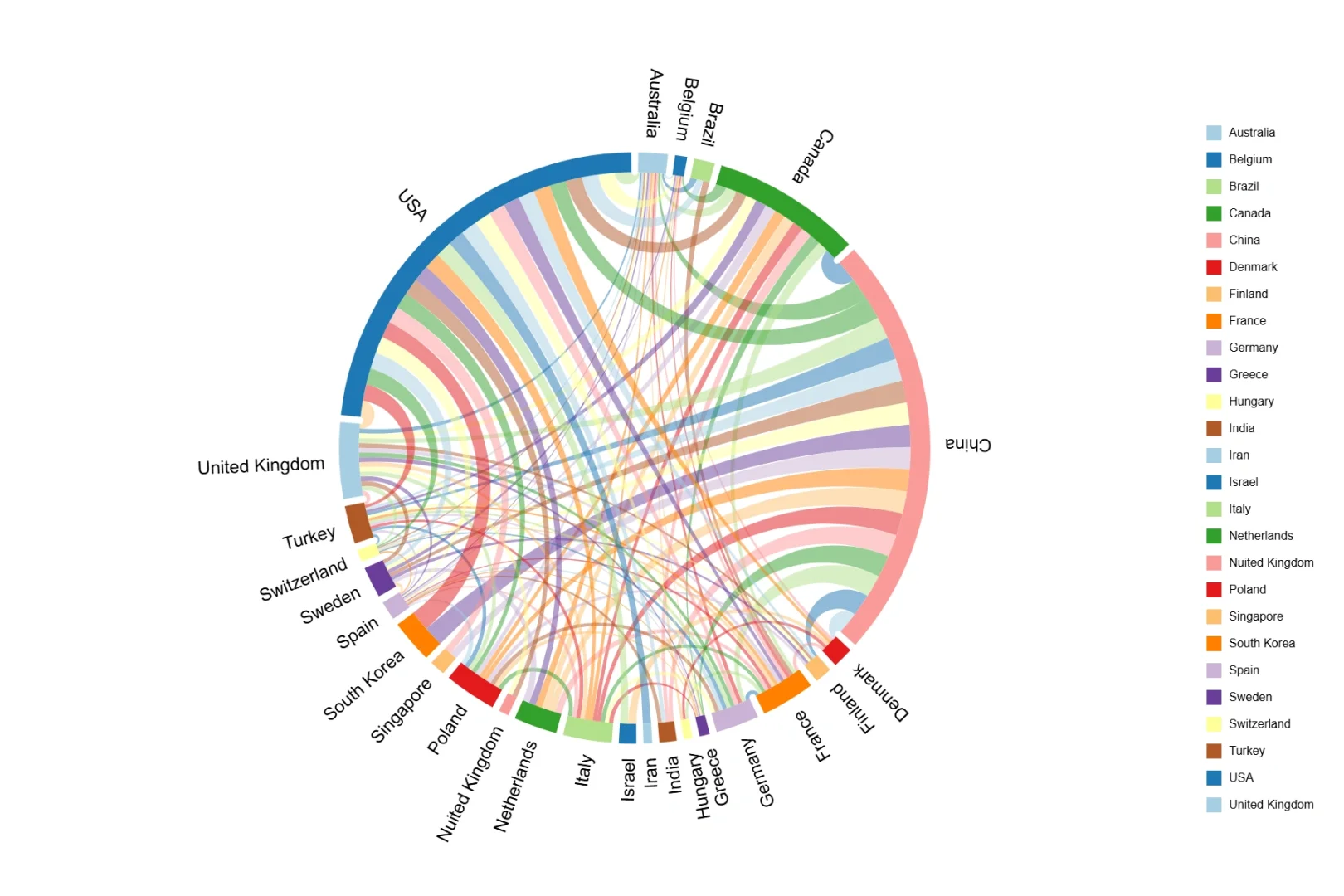
GSEA 富集图

作用

GSEA（Gene Set Enrichment Analysis）富集图用于分析基因集在特定生物学过程或通路中的富集情况，能够揭示基因表达变化的生物学意义。

读图

GSEA 富集图通常包括富集分数曲线、基因集的分布位置以及显著性结果等。富集分数曲线显示基因集在排序列表中的富集程度，基因集的分布位置用点表示，显著性结果用 p 值和 FDR 校正值表示。

参数

  • gene_sets，基因集数据库，如'c2.cp.kegg.v7.5.1.symbols.gmt'
  • msigdb，是否使用 MSigDB 数据库
  • figsize，图的大小
  • format，输出格式
  • no_plot，是否显示图。

示例代码

1
2
3
4
5
6
from gseapy import GSEA
# 运行 GSEA 分析
gsea_results = GSEA(data, cls=sample_labels, gene_sets='KEGG_2021_HUMAN', outdir='GSEA_Results', format='png', no_plot=False)

# 绘制 GSEA 富集图
gsea_results.plot_topTerms()