本问题的产生深切反映了没学到本质，做的偏LLM顶层，疏忽了理解原理。以后再不学技术上被基座和架构的佬们吊打，商业上产品基本的参数设定也不明白。多学多用多练吧。

问题

“在生产环境中，我们发现即使将 temperature 设置为 0，使用相同的输入，输出有时也会不同。可能的原因是什么？”

即使 temperature=0 且固定 seed，向 GPT-4 或 Claude 发送相同 prompt 仍可能得到不同输出，GPT-4 在30 次调用中可能产生 11-12 种不同的输出，这种非确定性程度远超浮点误差所能解释的范围。相比之下，早期的 davinci 模型（未使用 MoE 架构）则稳定得多。


理论预期

当 temperature=0 时，模型理论上应该进入贪婪解码模式（Greedy Decoding）：

  • 在每个生成步骤，模型选择概率最高的 token
  • 数学上，这是一个 argmax 操作，不涉及任何概率采样
  • 给定相同的输入和模型权重，每一步的 logits 应该完全相同
  • 因此，最终输出应该完全一致

数学表达：

$$
\text{next_token} = \arg\max_{i} \frac{\exp(\text{logits}_i / T)}{\sum_{j} \exp(\text{logits}_j / T)}
$$

当 $T = 0$ 时，上式退化为： $\text{next_token} = \arg\max_{i} \text{logits}_i$


原因

按重要性可以分为架构层面（MoE架构）、算法层面（浮点数精度、Tie-breaking机制）、框架层面（框架层面）和硬件层面（硬件异构性）。

MoE架构

这是导致 GPT-4 等模型输出差异的最主要原因。如果是面试，最关键的是回答MoE架构内容。

MoE架构概述


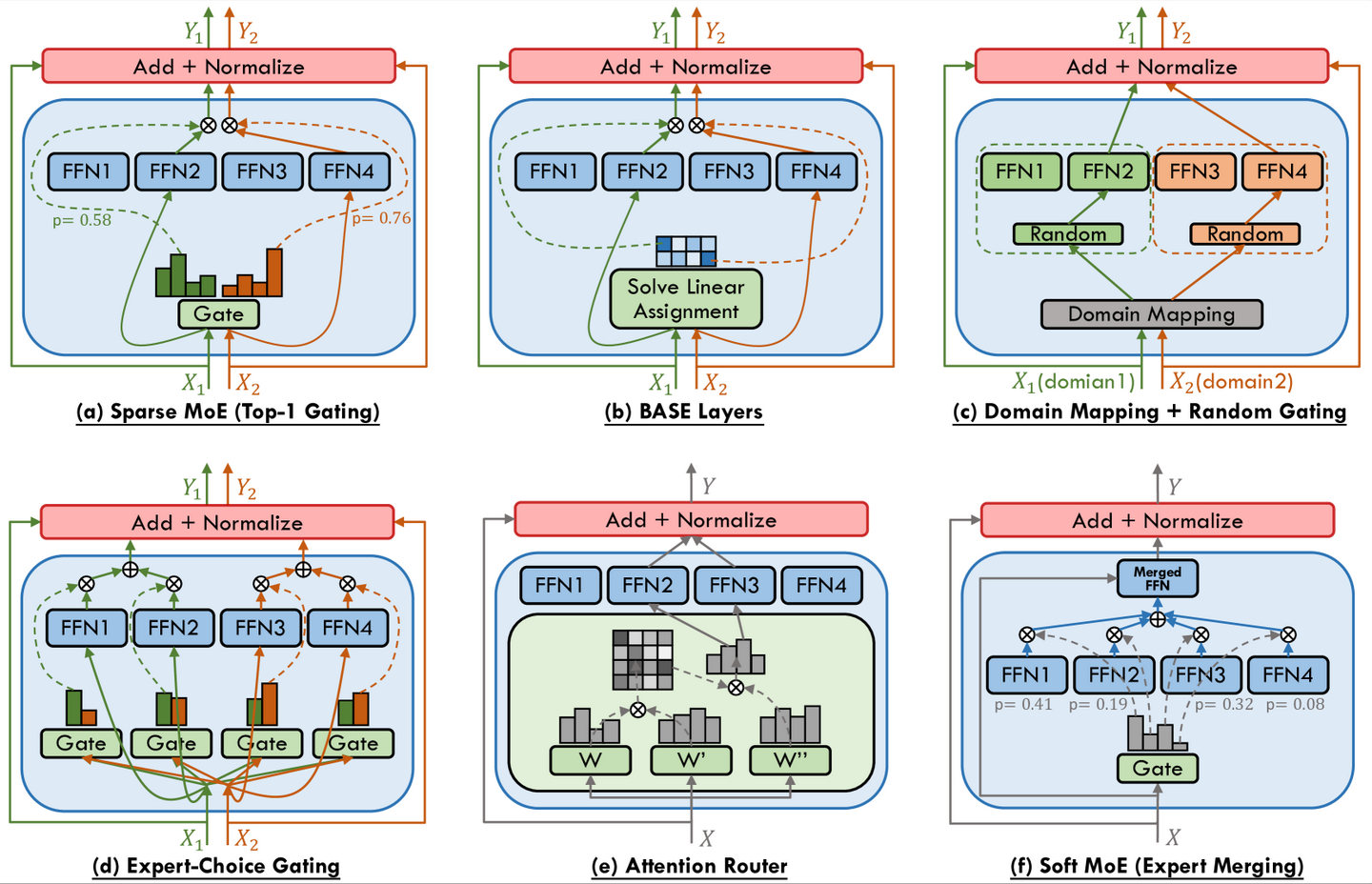
Mixture of Experts (MoE) 模型不是单一的大网络，而是由多个”专家网络”（Expert Networks）组成：

  • 每个专家是一个独立的 Feed-Forward Network (FFN)
  • 推理时，通过”门控机制”（Gating Mechanism）决定每个 token 应该路由到哪个专家
  • 为了效率，专家通常有容量限制（Capacity Limit），即一个专家同时只能处理有限数量的 token

数学表达：

对于 MoE 层，给定输入 $x$：

$$
\text{MoE}(x) = \sum_{i=1}^{E} G_i(x) \cdot \text{Expert}_i(x)
$$

其中：

  • $E$ 是专家数量
  • $G_i(x)$ 是路由权重，通常通过 softmax 归一化：$G_i(x) = \frac{\exp(g_i(x))}{\sum_{j=1}^{E} \exp(g_j(x))}$
  • $\text{Expert}_i(x)$ 是第 $i$ 个专家的输出

容量限制：

每个专家 $\text{Expert}_i$ 有容量 $C_i$，如果分配给它的 token 数量超过 $C_i$，超出的 token 会被路由到其他专家（负载均衡）。


批次级非确定性的产生

单请求场景：

对于单个用户请求，路由决策是确定的（假设其他因素不变）。

批处理场景：

API 服务提供商为了提高 GPU 利用率，会将多个用户请求批处理（Batching）在一起：

Batch = [User_A_request, User_B_request, User_C_request, ...]

问题产生：

当来自不同用户的 token 竞争同一个专家时：

  1. 容量竞争：如果 User A 的某个关键 token 原本应该路由到 Expert 1
  2. 批次影响：但如果 User B 的 token 也在同一批次中，且 Expert 1 的容量已满
  3. 路由改变：User A 的 token 可能被”挤出”，路由到 Expert 2
  4. 输出差异：即使两个专家都正常工作，它们的输出不同，导致生成结果不同

理论分析

根据相关论文，Sparse MoE 模型不再是序列级确定性（sequence-level deterministic），而是批次级确定性（batch-level deterministic）。这是 MoE 架构的本质特性：

  • 只有当整个批次在每次推理时都完全相同时，模型才会产生相同输出
  • 对于 API 用户而言，无法控制自己的请求会和哪些其他请求被批处理在一起
  • 因此，从用户视角看，输出是随机的

数学表达：

设 $B$ 为批次，$x$ 为输入序列，$y$ 为输出：$y = f_{\text{MoE}}(x, B)$

其中 $f_{\text{MoE}}$ 依赖于整个批次 $B$，而不仅仅是 $x$。

回到现象，这能解释使用了 MoE 架构的GPT-4容易产生不同输出，未使用 MoE 的 davinci 模型稳定得多。


浮点数精度

虽然 MoE 架构是主要原因，但底层还存在着浮点运算的非结合性这一基础技术原因。
面试的时候不能先回答这个，因为如果仅仅只有它不会造成那么大的variance。浮点精度问题在并行计算中的后果有一定关系，但不主要。不过，这是最容易想到的第一个原因，也是理解更深层问题的入口。

原理

经典示例：

1
2
3
4
5
6
7
8
# 示例 1：非结合性
(1 + 1e16) - 1e16  # 结果：0.0
1 + (1e16 - 1e16)  # 结果：1.0

# 示例 2：累加顺序的影响
import numpy as np
arr = np.array([1e10, 1, 1, 1, -1e10])
print(np.sum(arr))  # 可能因累加顺序不同而不同

数学原理：

IEEE 754 浮点数表示遵循： $x = (-1)^s \times m \times 2^e$

其中：

  • $s$ 是符号位
  • $m$ 是尾数（mantissa），$1 \leq m < 2$
  • $e$ 是指数（exponent）

由于尾数位数有限（单精度 23 位，双精度 52 位），当两个数量级差异很大的数相加时，较小的数可能被”吞掉”：

$$
\text{fl}(a + b) = \text{round}(a + b)
$$

其中 $\text{fl}(\cdot)$ 表示浮点表示，$\text{round}(\cdot)$ 表示舍入操作。


GPU并行计算

当 LLM 在 GPU 上执行前向传播时：

  1. 大规模并行矩阵运算：Attention 计算、FFN 计算等涉及大量并行操作
  2. 归约操作（Reduction Operations）：在计算 attention scores 时，可能需要对数千甚至数百万个数值求和

并行归约示例：

假设要计算 $S = \sum_{i=1}^{N} x_i$，GPU 将其分配给多个线程并行处理：

1
2
3
4
Thread 0: sum_0 = x_1 + x_2 + ... + x_{N/4}
Thread 1: sum_1 = x_{N/4+1} + ... + x_{N/2}
Thread 2: sum_2 = x_{N/2+1} + ... + x_{3N/4}
Thread 3: sum_3 = x_{3N/4+1} + ... + x_N

然后合并结果：$S = \text{sum}_0 + \text{sum}_1 + \text{sum}_2 + \text{sum}_3$

核心问题：由于线程调度的非确定性，合并顺序可能不同：

  • 情况 A：$S = (\text{sum}_0 + \text{sum}_1) + (\text{sum}_2 + \text{sum}_3)$
  • 情况 B：$S = (\text{sum}_0 + \text{sum}_2) + (\text{sum}_1 + \text{sum}_3)$

由于浮点数的非结合性，这两种情况可能产生不同的结果。


Attention计算

在 Transformer 的 Attention 机制中：

$$
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V
$$

其中 softmax 计算涉及：

$$
\text{softmax}(z_i) = \frac{\exp(z_i)}{\sum_{j=1}^{n} \exp(z_j)}
$$

当计算 $\sum_{j=1}^{n} \exp(z_j)$ 时，如果 $n$ 很大（如序列长度很长），并行归约的顺序会影响最终结果，进而影响 softmax 的输出，最终影响 logits。

数值稳定性问题：

实际实现中，softmax 通常使用数值稳定版本：

$$
\text{softmax}(z_i) = \frac{\exp(z_i - \max(z))}{\sum_{j=1}^{n} \exp(z_j - \max(z))}
$$

但即使如此，$\max(z)$ 的并行计算和后续的归约操作仍然受浮点非结合性影响。

影响程度

上述浮点数的非结合性在 GPU 并行计算和 Attention 计算中被放大，为 MoE 架构层面的非确定性提供了基础。但单独的浮点误差不足以解释 GPT-4 如此大的输出差异。具体影响程度如下：

  • 通常影响：差异出现在第 15 位小数左右
  • 关键问题：当两个 token 的 logits 非常接近时，这些微小差异足以改变 argmax 的结果
  • 累积效应：在自回归生成中，每一步的微小差异会累积，导致最终输出显著不同

框架层面

除了 MoE 架构和浮点运算这两个主要因素外，还有框架层面和硬件层面的非确定性因素，它们会叠加在基础问题上，进一步放大差异。

PyTorch非确定性操作

现代深度学习框架为了性能优化，默认不保证确定性。

PyTorch 非确定性操作示例：

  1. torch.nn.functional.conv2d：使用 cuDNN 时，算法选择可能非确定
  2. torch.nn.functional.max_pool2d：当多个值相等时，选择可能非确定
  3. torch.bmm（批量矩阵乘法）：使用 cuBLAS 时可能非确定
  4. torch.nn.functional.dropout：即使设置 training=False，某些实现仍可能非确定

强制确定性的方法：

1
2
3
4
5
6
7
8
9
10
11
12
import torch
import os

# 设置确定性算法
torch.use_deterministic_algorithms(True)

# 设置 cuDNN 确定性
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False

# 设置 cuBLAS 工作空间（避免非确定性）
os.environ['CUBLAS_WORKSPACE_CONFIG'] = ':4096:8'

性能代价：

  • 确定性算法通常比非确定性算法慢 2-10 倍
  • 在生产环境中，性能优先，因此很少启用确定性模式

CUDA层面非确定性

线程调度：

GPU 的线程调度是非确定性的，这影响：

  1. 归约操作的顺序：如前文所述
  2. 内存访问模式：可能影响缓存行为
  3. 原子操作：虽然原子操作本身是确定的，但不同线程的执行顺序可能不同

cuDNN 算法选择：

cuDNN 会自动选择”最优”算法，但选择可能因运行环境而异：

  • GPU 型号
  • cuDNN 版本
  • 输入形状
  • 工作空间大小

数值库实现差异

不同的数值库（BLAS、cuBLAS、MKL）可能对同一操作有不同的实现：

  • 矩阵乘法：不同的分块策略、不同的累加顺序
  • 激活函数：不同的近似方法（如 tanh、sigmoid）
  • 归一化操作：LayerNorm、BatchNorm 的实现细节

框架层面的非确定性通常是为了性能优化而做出的权衡。虽然可以通过设置强制确定性模式来缓解，但这会显著牺牲性能（通常慢 2-10 倍），在生产环境中很少采用。


硬件异构性

GPU架构差异

云服务提供商通常使用异构 GPU 集群：

GPU 型号 架构 CUDA 核心数 Tensor 核心数 显存 (HBM) 带宽 NVLink 主要应用
A100 Ampere 6912 432 40GB/80GB 1.6TB/s 支持 AI训练、推理、HPC
H100 Hopper 16896 528 80GB 3.35TB/s 支持 AI训练、HPC、Transformer Engine
A800 Ampere 6912 432 40GB/80GB 受限 受限 中国市场AI计算
H800 Hopper 16896 528 80GB 受限 受限 中国市场大规模AI训练

影响：

  • 用户的请求可能这次落在 H100 GPU 上，下次落在 A100 GPU 上
  • 虽然这些 GPU 兼容，但架构细节、CUDA 实现、甚至驱动版本可能不同
  • 这可能导致相同计算在不同硬件上产生略微不同的结果

Transformer Engine影响

H100 引入了 Transformer Engine，使用 FP8 精度进行训练和推理：

  • FP8 格式：8 位浮点数，有两种格式（E4M3 和 E5M2）
  • 动态缩放：根据数据范围动态调整缩放因子
  • 精度差异：与 FP16/BF16 相比，FP8 的舍入行为可能不同

数学表达：

FP8 表示：

$$
x_{\text{FP8}} = \text{quantize}(x_{\text{FP32}}, \text{scale})
$$

其中 quantize 操作可能因硬件实现而异。


模型并行影响

对于 GPT-4 这样的大模型，无法放在单个 GPU 上，必须进行模型并行（Model Parallelism）：

  • 模型被分割到多个 GPU 甚至多台机器上
  • 分布式推理涉及跨设备通信
  • 数据聚合顺序：不同设备返回结果的顺序可能因网络延迟而异
  • 通信延迟：可能影响同步点，进而影响计算顺序

示例：

1
2
3
4
GPU 0: Layer 0-10
GPU 1: Layer 11-20
GPU 2: Layer 21-30
GPU 3: Layer 31-40

在层间通信时，如果 GPU 1 和 GPU 2 的通信延迟不同，可能导致不同的聚合顺序。


影响程度

虽然硬件层面的影响相比 MoE 的批次效应较小，但仍会：

  • 在浮点误差的基础上进一步放大差异
  • 与框架层面的非确定性叠加
  • 在关键决策点（如两个 token logits 非常接近时）改变结果

框架层面和硬件层面的非确定性会叠加在 MoE 和浮点运算的基础上，形成多层叠加效应，进一步放大输出差异。


Tie-breaking机制

上述各种因素（MoE 路由、浮点误差、框架实现、硬件差异）的叠加，还会导致 Tie-breaking 机制的不稳定性。

理论

理论上，argmax 应该有固定的平局处理规则（tie-breaking rule），例如：

  • 选择索引较小的 token
  • 选择 ID 较小的 token

数学表达：

$$
\text{argmax}(x) = \min{i : x_i = \max(x)}
$$


实际

但在实际实现中，由于前述各种因素：

  1. 浮点误差：两个 token 的 logits 可能因浮点误差而在不同运行中交换位置
  2. 硬件差异：不同硬件上的计算可能导致不同情况
  3. 批次影响：MoE 路由可能改变 logits 的相对大小

示例：

1
2
3
4
5
运行 1: logits = [0.5000001, 0.5000000, 0.3, ...]
        → 选择 token 0

运行 2: logits = [0.5000000, 0.5000001, 0.3, ...]  (因浮点误差)
        → 选择 token 1

在自回归生成中有累积效应：

  1. 第一步：微小的差异导致选择了不同的 token
  2. 后续步骤：不同的 token 作为输入，导致完全不同的生成路径
  3. 指数级发散：差异在每一步都可能放大

数学表达：

设 $y_t$ 为第 $t$ 步的输出，$x_t$ 为第 $t$ 步的输入：

$$
y_t = \arg\max(\text{LLM}(x_t))
$$

如果 $y_t$ 不同，则 $x_{t+1} = [x_t, y_t]$ 也不同，导致后续所有步骤都不同。



应对策略

业务层面策略

对于关键业务场景：

  • 不要依赖精确字符串匹配：设计更”鲁棒”的解析逻辑
  • 优先语义正确性：而非字面一致性
  • 使用解析器：如果从 LLM 输出中提取结构化信息，使用正则表达式或专门的 parser，而不是期望格式每次都完全相同

示例：

1
2
3
4
5
6
7
8
9
10
# 不好的做法
if llm_output == "Yes, the user is eligible.":
    return True

# 更好的做法
if "eligible" in llm_output.lower() or "yes" in llm_output.lower():
    return True

# 或使用专门的解析器
result = parse_eligibility(llm_output)  # 处理多种表达方式

部署开源模型策略

使用确定性算子库：

  • 考虑使用”批次不变”（batch-invariant）的算子库
  • 但这通常牺牲性能

PyTorch 确定性设置：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import torch
import os
import random
import numpy as np

# 设置随机种子
def set_seed(seed):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    
# 确定性算法
torch.use_deterministic_algorithms(True)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False

# cuBLAS 工作空间
os.environ['CUBLAS_WORKSPACE_CONFIG'] = ':4096:8'

# 注意：这会影响性能，可能慢 2-10 倍

MoE 模型的特殊处理：

  • 如果可能，使用单批次推理（batch_size=1）
  • 但这会显著降低吞吐量
  • 对于 MoE 模型，批次级非确定性是架构固有的，难以完全消除

评估和测试策略

考虑固有不确定性：

  • 多次运行取中位数：运行多次，取中位数或最常见的输出
  • Self-Consistency：生成多个候选，选择最一致的答案
  • 不要假设单一输出是唯一正确答案：接受输出的多样性

Self-Consistency 示例：

1
2
3
4
5
6
7
8
9
def self_consistency_predict(prompt, n_samples=5):
    candidates = []
    for _ in range(n_samples):
        output = model.generate(prompt, temperature=0)
        candidates.append(output)
    
    # 选择最常见的答案
    from collections import Counter
    return Counter(candidates).most_common(1)[0][0]

评估指标调整：

  • 使用语义相似度而非精确匹配
  • 对于结构化输出，使用字段级匹配而非全文匹配



参考文献

论文

  • MoE 架构：

    • Shazeer et al., “Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer” (2017)
    • Fedus et al., “Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity” (2021)

  • 数值稳定性：

    • Higham, “Accuracy and Stability of Numerical Algorithms” (2002)
    • Blanchard et al., “Numerical stability of deterministic parallel reduction” (2020)

文档