机器学习回归算法

参考：
- https://www.showmeai.tech/
- 小红书 @科研百味

监督学习（Supervised Learning）：训练集有标记信息，学习方式有分类和回归。
【注意：逻辑回归（Logistic Regression) 虽然名为回归，但常用于分类。它是一种用于分类的监督学习算法，基于逻辑函数(Sigmoid)。参考：ML分类。】

线性回归

Linear Regression

原理

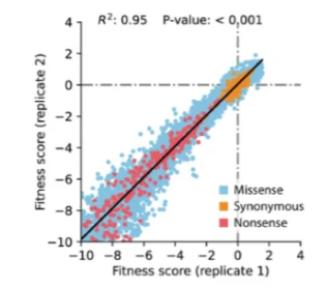
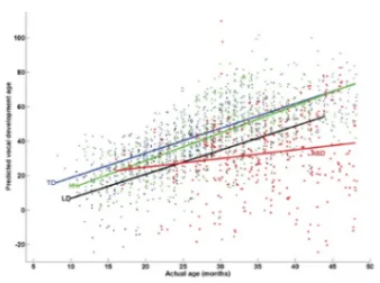
通过线性组合说明自变量因变量关系。一般是一个自变量与一个因变量(左图)，多重线性回归就是多个自变量与一个因变量(右图)。

通过最小化残差平方和（RSS）寻找最佳线性拟合：线性回归是最基础的回归方法，用于建立自变量和因变量之间的线性关系模型。它通过最小化预测值与实际值之间的平方误差来找到最佳拟合线。

数学表达：
$$ y = \beta_0 + \beta_1x_1 + \cdots + \beta_nx_n + \epsilon $$
其中：

$\beta_0$ 是截距项
$\beta_1$ 到 $\beta_n$ 是回归系数
$\epsilon \sim \mathcal{N}(0, \sigma^2)$ 是误差项，服从正态分布

最小化目标函数：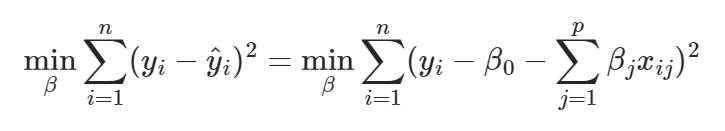

特点

需满足线性、独立性、正态性、同方差性假设
模型简单透明（Interpretability）
对异常值敏感

优缺点

优点：

简单易懂，易于解释。
计算效率高

缺点：

对数据要求较高，需满足线性关系、正态性、同方差性等假设。
无法处理非线性关系。
对多重共线性敏感

应用领域

经济学（房价预测）、医学（剂量反应分析）、工业（质量控制）

代码示例

from sklearn.linear_model import LinearRegression
# 创建线性回归模型实例
# fit_intercept: 是否计算截距项
# n_jobs: 并行计算的作业数，-1表示使用所有CPU
# copy_X: 是否复制X，如果为False则可能被覆盖
model = LinearRegression(fit_intercept=True, n_jobs=-1, copy_X=True)
# 训练模型
# X_train: 训练数据特征
# y_train: 训练数据标签
model.fit(X_train, y_train)
# 输出模型参数
# coef_: 回归系数
# intercept_: 截距项
print(f"回归系数: {model.coef_}, 截距: {model.intercept_}")

多项式回归

Polynomial Regression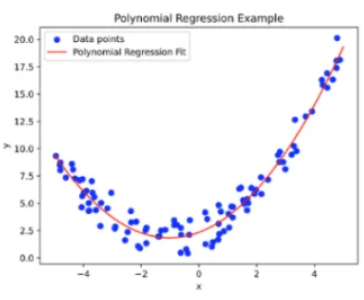

原理

通过特征升维拟合非线性关系：多项式回归是对线性回归的扩展，用于处理非线性关系。通过将原始特征转换为多项式特征，可以在保持模型线性性的同时捕捉非线性关系。

数学表达：
$$ y = \beta_0 + \beta_1x + \beta_2x^2 + \cdots + \beta_nx^n + \epsilon $$

关键点：

特征转换：将原始特征 $x$ 转换为 $[x, x^2, …, x^n]$
保持线性性：虽然输入特征是非线性的，但模型参数 $\beta$ 仍然是线性的
过拟合风险：随着阶数 $n$ 的增加，模型复杂度显著提高

特点

通过特征工程扩展线性模型
需谨慎选择多项式阶数（Degree）
易产生过拟合

优缺点

优点：对非线性关系拟合能力强。
缺点：易过拟合，计算复杂度随次数增加而上升。外推能力差。

应用领域

物理学（运动轨迹预测）、工程学（材料应力分析）

代码示例

from sklearn.preprocessing import PolynomialFeatures
# 创建多项式特征转换器
# degree: 多项式的最高次数
# interaction_only: 是否只生成交互项
# include_bias: 是否包含偏置项（常数项）
poly = PolynomialFeatures(degree=3, interaction_only=False, include_bias=True)
# 转换特征
X_poly = poly.fit_transform(X)
# 创建并训练线性回归模型
model = LinearRegression().fit(X_poly, y)

正则化回归

Regularized Regression

正则化原理

正则化是一种通过添加惩罚项来防止模型过拟合的技术。主要有两种形式：

L1正则化（LASSO）
- 添加系数的绝对值之和 $\sum |w_j|$ 作为惩罚项
- 数学形式：$\Omega(w)$ = $||w||1$ = $\sum{j=1}^p |w_j|$
- 几何意义：
  - 在参数空间中形成一个菱形（二维）或超菱形（高维）的约束区域
  - 最优解倾向于落在约束区域的顶点上
  - 顶点处某些系数为0，产生稀疏解
- 特点：
  - 会产生稀疏解（部分系数变为0）
  - 具有特征选择能力
  - 对异常值敏感
  - 适合高维特征选择
- 应用场景：
  - 特征数量远大于样本数量
  - 需要特征选择
  - 数据中存在大量无关特征
L2正则化（岭回归）
- 添加系数的平方和 $\sum w_j^2$ 作为惩罚项
- 数学形式：$\Omega(w) = \frac{1}{2}||w||^2_2 = \frac{1}{2}\sum_{j=1}^p w_j^2$
- 几何意义：
  - 在参数空间中形成一个圆形（二维）或球形（高维）的约束区域
  - 最优解会落在约束区域的边界上
  - 倾向于产生较小的系数值
- 特点：
  - 对所有系数进行等比例收缩
  - 不会将系数压缩到0
  - 对异常值不敏感
  - 适合处理多重共线性问题
- 应用场景：
  - 特征之间存在高度相关性
  - 样本数量小于特征数量
  - 需要稳定系数估计

正则化效果对比

特性	L1正则化	L2正则化
解的特性	稀疏解	非稀疏解
特征选择	支持	不支持
计算效率	较慢	较快
适用场景	特征选择	多重共线性
几何约束	菱形/超菱形	圆形/超球体
系数收缩	不均匀	均匀
对异常值	敏感	不敏感

正则化强度选择
- $\alpha$ 参数控制正则化强度
- 过大的 $\alpha$：
  - L1：过多特征被压缩到0
  - L2：所有系数过度收缩
- 过小的 $\alpha$：
  - 正则化效果不明显
  - 可能无法解决过拟合
- 选择方法：
  - 交叉验证
  - 网格搜索
  - 基于验证集性能
实际应用建议
- 数据预处理：
  - 特征标准化
  - 处理缺失值
  - 异常值检测
- 模型选择：
  - 特征数量少：优先考虑L2
  - 特征数量多：优先考虑L1
  - 特征相关性强：考虑弹性网络
- 调参策略：
  - 从小到大的 $\alpha$ 值范围
  - 结合交叉验证
  - 监控模型复杂度

LASSO回归

原理

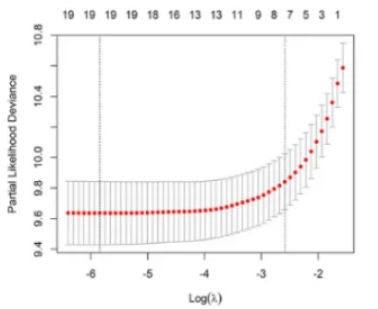
L1正则化实现特征选择：LASSO回归通过L1正则化实现特征选择，能够产生稀疏解。当特征数量很多时，LASSO可以帮助识别重要特征。

目标函数：
$$ \text{Loss} = \text{RSS} + \alpha\sum_{j=1}^p|\beta_j| $$
其中：

$|\beta_j|$ 是L1正则化项
当 $\alpha$ 足够大时，某些系数会被压缩到0
这种特性使得LASSO具有自动特征选择的能力

特点

产生稀疏解（Sparsity）
适用于高维特征筛选
当特征数量大于样本数量时特别有用
对异常值比较敏感

代码示例

from sklearn.linear_model import Lasso
# LASSO回归（L1正则化）
# alpha: 正则化强度
# max_iter: 最大迭代次数
# tol: 优化的容差
lasso_model = Lasso(alpha=0.1, max_iter=1000, tol=1e-4)
lasso_model.fit(X, y)

岭回归

Ridge Regression

原理

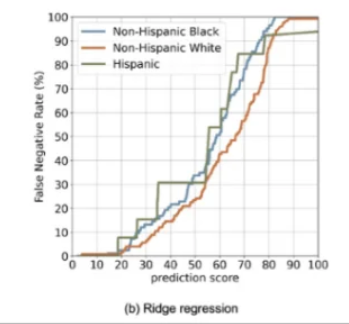
L2正则化解决多重共线性：岭回归通过引入L2正则化项来解决多重共线性问题。当特征之间存在高度相关性时，普通最小二乘估计可能不稳定，岭回归通过惩罚大的系数值来稳定估计。

目标函数：
$$ \text{Loss} = \text{RSS} + \alpha\sum_{j=1}^p\beta_j^2 $$
其中：

RSS是残差平方和
$\alpha$ 是正则化强度参数
$\sum_{j=1}^p\beta_j^2$ 是L2正则化项

特点

收缩系数但不置零
对病态数据鲁棒
当特征高度相关时，系数估计更稳定
随着$\alpha$增大，所有系数都会向0收缩，但不会等于0

代码示例

from sklearn.linear_model import Ridge
# Ridge回归（L2正则化）
# alpha: 正则化强度，越大则正则化效果越强
# fit_intercept: 是否计算截距
# solver: 优化算法，可选：
#   - 'auto': 自动选择最佳算法
#   - 'svd': 奇异值分解，适合小数据集
#   - 'cholesky': Cholesky分解，适合特征数小于样本数的情况
#   - 'lsqr': 最小二乘QR分解，适合大规模数据
#   - 'sparse_cg': 共轭梯度法，适合稀疏矩阵
#   - 'sag': 随机平均梯度下降，适合大数据集
#   - 'saga': SAG的改进版本，支持非平滑惩罚项
ridge_model = Ridge(alpha=0.5, fit_intercept=True, solver='auto')
ridge_model.fit(X, y)

弹性网络回归

Elastic Net Regression

原理

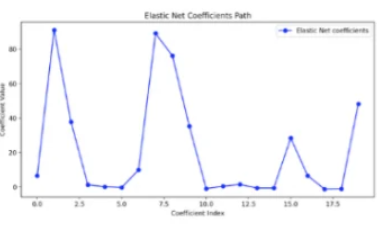
结合L1/L2正则化：弹性网络结合了L1和L2正则化的优点，特别适合处理高度相关的特征。它既具有LASSO的特征选择能力，又具有岭回归的稳定性。

目标函数：
$$ \text{Loss} = \text{RSS} + \alpha\rho\sum|\beta_j| + \alpha(1-\rho)\sum\beta_j^2 $$
其中：

$\rho$ 控制L1和L2正则化的比例
当 $\rho=1$ 时退化为LASSO
当 $\rho=0$ 时退化为岭回归
$\alpha$ 控制整体正则化强度

特点

结合了L1和L2正则化的优点
可以处理高度相关的特征
在特征数量大于样本数量时表现更好
比LASSO更稳定，比岭回归更具特征选择能力

对比总结

类型	正则项	特点	最佳场景
Ridge	L2	系数收缩	多重共线性数据
LASSO	L1	特征选择	高维特征筛选
Elastic Net	L1+L2	平衡两者	高度相关特征

代码示例

from sklearn.linear_model import ElasticNet
# 弹性网络（结合L1和L2正则化）
# alpha: 正则化强度
# l1_ratio: L1正则化比例，范围[0,1]
# max_iter: 最大迭代次数
elastic_model = ElasticNet(alpha=0.1, l1_ratio=0.5, max_iter=1000)
elastic_model.fit(X, y)

分位数回归

Quantile Regression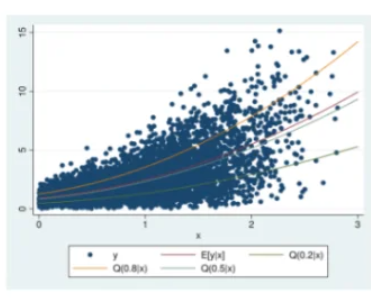

原理

通过估计相应变量的条件分位数建模，能够捕捉数据异质性。
最小化非对称损失函数：分位数回归是对传统均值回归的扩展，用于估计条件分位数。它不假设误差项服从正态分布，对异常值更稳健。

目标函数：
$$ \min_{\beta} \sum_{i=1}^n \rho_\tau(y_i - x_i^T\beta) $$
其中：

$\rho_\tau(u) = u(\tau - I(u<0))$ 是分位数损失函数
$\tau$ 是目标分位数（如0.5表示中位数）
$I(u<0)$ 是指示函数（当u<0时为1，否则为0）

特点：

可以估计整个条件分布,估计条件分位数（Conditional Quantiles）
对异常值鲁棒(不敏感)
不需要误差项分布假设

传统线性回归关注的是条件均值（mean） ，即预测值的平均值。
分位数回归关注的是条件分位数（quantile） ，比如中位数（50%分位数）、25%分位数、75%分位数等。通过估计不同分位数的回归系数，可以更全面地描述因变量的条件分布。

优缺点

优点	缺点
全面描述响应分布	计算复杂度高
处理异方差数据	参数解释复杂
无分布假设	需要大样本量

应用领域

经济学（收入不平等研究）、气象学（极端天气预测）、金融(风险评估)、医学(药物剂量反应）

代码示例

from statsmodels.regression.quantile_regression import QuantReg
# 创建分位数回归模型
# q: 分位数，范围[0,1]
# fit_intercept: 是否计算截距
model = QuantReg(y, X).fit(q=0.85, fit_intercept=True)  # 85%分位数

树模型回归

Tree-based Regression

决策树回归

参考：https://www.showmeai.tech/article-detail/190

原理

递归划分特征空间，叶节点输出均值:决策树回归通过递归地将特征空间划分为不重叠的区域，每个区域对应一个预测值。

主流的决策树算法有：

ID3：基于信息增益来选择分裂属性（每步选择信息增益最大的属性作为分裂节点，树可能是多叉的）。
C4.5：基于信息增益率来选择分裂属性（每步选择信息增益率最大的属性作为分裂节点，树可能是多叉的）。
CART：基于基尼系数来构建决策树（每步要求基尼系数最小，树是二叉的）。
其中CART树全称Classification And Regression Tree，即可以用于分类，也可以用于回归，这里指的**回归树就是 CART 树，ID3和C4.5不能用于回归问题。

分裂准则：

最小化MSE：$ \text{MSE} = \frac{1}{N}\sum(y_i - \bar{y})^2 $
在每个节点选择最优分裂特征和分裂点
递归地构建树直到满足停止条件

代码示例

# 决策树回归
from sklearn.tree import DecisionTreeRegressor
# max_depth: 树的最大深度
# min_samples_split: 分裂内部节点所需的最小样本数
# min_samples_leaf: 叶节点所需的最小样本数
# criterion: 分裂标准，可选：
#   - 'mse': 均方误差，最常用的回归标准
#   - 'friedman_mse': Friedman改进的MSE，考虑了潜在的不纯度减少
dt_model = DecisionTreeRegressor(
    max_depth=5,
    min_samples_split=2,
    min_samples_leaf=1,
    criterion='mse'
)
dt_model.fit(X, y)

随机森林

Random Forest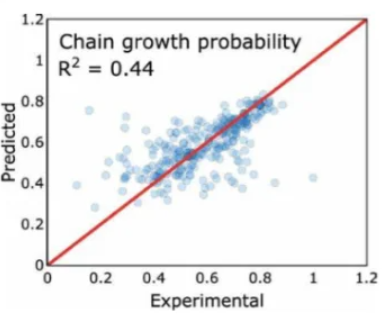

原理

Bootstrap聚合多棵决策树：随机森林通过Bootstrap采样构建多棵决策树，并通过投票或平均得到最终预测。它解决了单棵决策树的高方差问题。

预测公式：
$$ \hat{y} = \frac{1}{B}\sum_{b=1}^B T_b(x) $$
其中：

$B$ 是树的数量
$T_b(x)$ 是第b棵树的预测
每棵树使用随机采样的数据和特征子集

代码示例

# 随机森林回归
from sklearn.ensemble import RandomForestRegressor
# n_estimators: 树的数量
# max_depth: 树的最大深度
# min_samples_split: 分裂内部节点所需的最小样本数
# n_jobs: 并行计算的作业数
rf_model = RandomForestRegressor(
    n_estimators=100,
    max_depth=10,
    min_samples_split=2,
    n_jobs=-1
)
rf_model.fit(X, y)

梯度提升

Gradient Boosting

原理

迭代拟合残差：梯度提升通过迭代地拟合残差来构建强学习器。每一步都训练一个新的弱学习器(如决策树)来拟合当前模型的残差,根据前一轮预测误差调整后续学习器权重以改进模型。

迭代公式：
$$ F_m(x) = F_{m-1}(x) + \gamma_m h_m(x) $$
其中：

$F_m(x)$ 是第m次迭代后的模型
$h_m(x)$ 是第m个弱学习器
$\gamma_m$ 是学习率
伪残差：$ r_{im} = -\frac{\partial L(y_i,F(x_i))}{\partial F(x_i)} $

代码示例

# GBDT回归
from sklearn.ensemble import GradientBoostingRegressor
# n_estimators: 提升阶段的数量
# learning_rate: 学习率
# max_depth: 树的最大深度
# min_samples_split: 分裂内部节点所需的最小样本数
gbdt_model = GradientBoostingRegressor(
    n_estimators=100,
    learning_rate=0.1,
    max_depth=3,
    min_samples_split=2
)
gbdt_model.fit(X, y)

对比总结

模型	特点	优势	缺陷
决策树	单棵树	解释性强	高方差
随机森林	Bagging	抗过拟合	计算资源大
梯度提升	Boosting	高精度	超参敏感

XGBoost

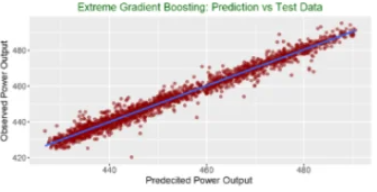
原理

目标函数加入正则项：XGBoost是对梯度提升的改进，通过引入正则化项和二阶导数信息来提高模型性能(防止过拟合&支持并行计算)。

目标函数：
$$ \text{Obj} = \sum L(y_i,\hat{y}_i) + \sum\Omega(f_k) $$
其中：

$L(y_i,\hat{y}_i)$ 是损失函数
$\Omega(f) = \gamma T + \frac{1}{2}\lambda||w||^2$ 是正则化项
$T$ 是叶子节点数
$w$ 是叶子节点权重

特点：

使用二阶泰勒展开近似损失函数
通过正则化控制模型复杂度
支持并行计算和稀疏特征

代码示例

# XGBoost
import xgboost as xgb
# 创建DMatrix数据格式
dtrain = xgb.DMatrix(X, label=y)
# 设置参数
params = {
    'objective': 'reg:squarederror',  # 回归目标函数
    'max_depth': 5,                   # 树的最大深度
    'learning_rate': 0.1,             # 学习率
    'subsample': 0.8,                 # 样本采样比例
    'colsample_bytree': 0.8,          # 特征采样比例
    'min_child_weight': 1,            # 最小子节点权重
    'gamma': 0                        # 分裂所需的最小损失减少
}
# 训练模型
# num_boost_round: 提升轮数
# evals: 评估数据集
# early_stopping_rounds: 早停轮数
xgb.train(params, dtrain, num_boost_round=100)

LightGBM

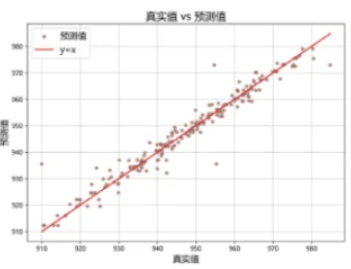
优化技术

Gradient-based One-Side Sampling (GOSS)
- 原理：
  - 基于梯度的单边采样，保留大梯度的样本，随机采样小梯度的样本
  - 大梯度样本对信息增益贡献大，小梯度样本贡献小
- 优势：
  - 减少数据量，加快训练速度
  - 保持模型精度
  - 降低内存使用
- 实现方式：
  - 按梯度绝对值排序
  - 保留top a%的大梯度样本
  - 随机采样b%的小梯度样本
  - 对小梯度样本的权重进行放大(1-a)/b倍
Exclusive Feature Bundling (EFB)
- 原理：
  - 将互斥特征（不同时取非零值的特征）捆绑在一起
  - 减少特征数量，降低内存消耗
- 优势：
  - 减少特征数量
  - 降低内存使用
  - 加快训练速度
- 实现方式：
  - 构建特征冲突图
  - 使用贪心算法进行特征捆绑
  - 将捆绑后的特征视为一个特征
Histogram-based Algorithm
- 原理：
  - 将连续特征离散化为直方图
  - 使用直方图进行特征分裂
- 优势：
  - 减少内存使用
  - 加快训练速度
  - 提高缓存命中率
Leaf-wise Tree Growth
- 原理：
  - 每次选择增益最大的叶子节点进行分裂
  - 不同于传统的level-wise生长方式
- 优势：
  - 更好的精度
  - 更快的收敛速度
  - 更少的模型复杂度

性能对比

指标	XGBoost	LightGBM
训练速度	中等	极快
内存占用	高	低
准确率	高	相当
类别特征	需编码	原生支持

代码示例

# LightGBM
import lightgbm as lgb
# 创建数据集
dataset = lgb.Dataset(X, label=y)
# 设置参数
params = {
    'objective': 'regression',         # 回归目标函数
    'num_leaves': 31,                 # 叶子节点数
    'learning_rate': 0.05,            # 学习率
    'feature_fraction': 0.8,          # 特征采样比例
    'bagging_fraction': 0.8,          # 样本采样比例
    'bagging_freq': 5,                # 采样频率
    'min_data_in_leaf': 20            # 叶子节点最小样本数
}
# 训练模型
lgb.train(params, dataset, num_boost_round=100)

支持向量回归

Support Vector Regression,SVR

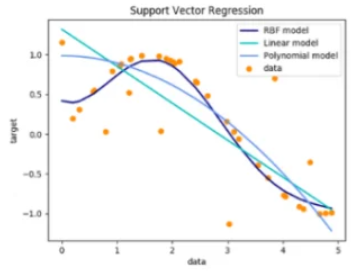
原理

在特征空间中构建超平面以最小化预测误差，最大化超平面与数据之间的距离。
最大化间隔带（$\epsilon$-insensitive tube）：SVR通过构建一个间隔带（$\epsilon$-tube）来拟合数据，只惩罚落在间隔带外的样本。这种方法对高维数据有效，对异常值具有很好的鲁棒性。

目标函数：
$$ \min \frac{1}{2}||w||^2 + C\sum(\xi_i+\xi_i^*) $$
约束条件：
$$ |y_i - w^Tx_i - b| \leq \epsilon + \xi_i $$
其中：

$w$ 是权重向量
$C$ 是惩罚参数
$\xi_i$ 和 $\xi_i^*$ 是松弛变量
$\epsilon$ 是间隔带宽度

核技巧———径向基函数（RBF）：
$$ K(x_i,x_j) = \exp(-\gamma||x_i-x_j||^2) $$
通过核函数将数据映射到高维空间，实现非线性回归。

优缺点

优点	缺点
高维空间有效	内存消耗大
非线性建模	参数调优复杂
鲁棒性强	解释性差

应用领域

金融时间序列预测、工业过程控制

代码示例

from sklearn.svm import SVR
# 创建SVR模型
# kernel: 核函数类型，可选：
#   - 'linear': 线性核，适合线性可分的数据
#   - 'poly': 多项式核，适合非线性数据，可调整多项式阶数
#   - 'rbf': 径向基函数核，最常用的核函数，适合大多数非线性问题
#   - 'sigmoid': sigmoid核，类似神经网络的激活函数
# C: 正则化参数
# gamma: 核系数
# epsilon: epsilon-tube参数
model = SVR(
    kernel='rbf',
    C=100,
    gamma=0.1,
    epsilon=0.1,
    tol=1e-3,           # 优化的容差
    max_iter=-1         # 最大迭代次数，-1表示无限制
)
model.fit(X_scaled, y)

神经网络回归

Neural Network Regression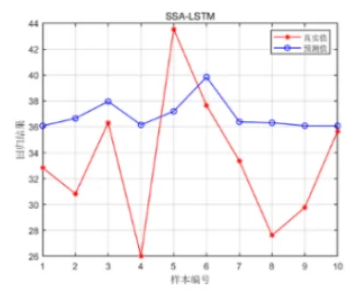

原理

通过反向传播算法优化模型参数。
多层感知机（MLP）结构：神经网络回归通过多层非线性变换来学习复杂的函数关系。它能够自动学习特征表示，具有很强的表达能力。

网络结构：
$$ \hat{y} = \sigma(W^{(L)}\cdots\sigma(W^{(1)}X + b^{(1)}) + b^{(L)}) $$
其中：

$W^{(l)}$ 是第l层的权重矩阵
$b^{(l)}$ 是第l层的偏置向量
$\sigma$ 是激活函数（如ReLU）

优化算法
Adam优化器：自适应学习率

注意事项

需特征缩放（Feature Scaling）
Dropout防止过拟合
早停法（Early Stopping）

特点：

通过反向传播算法优化参数
使用梯度下降最小化损失函数
可以学习任意复杂的函数关系

优缺点

优点：对非线性关系拟合能力强，能处理复杂数据模式。
缺点：模型复杂，训练时间长，解释较困难。

代码示例

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.callbacks import EarlyStopping

# 创建模型
model = Sequential([
    # 第一层：64个神经元，ReLU激活函数
    Dense(64, activation='relu', input_shape=(X.shape[1],)),
    # 第二层：32个神经元ReLU激活函数
    Dense(32, activation='relu'),
    # 输出层：1个神经元，线性激活函数
    Dense(1)
])

# 编译模型
# optimizer: 优化器
# loss: 损失函数
# metrics: 评估指标
model.compile(
    optimizer=Adam(learning_rate=0.001),
    loss='mse',
    metrics=['mae']
)

# 早停回调
early_stopping = EarlyStopping(
    monitor='val_loss',    # 监控验证集损失
    patience=10,           # 容忍轮数
    restore_best_weights=True  # 恢复最佳权重
)

# 训练模型
# epochs: 训练轮数
# batch_size: 批次大小
# validation_split: 验证集比例
# callbacks: 回调函数列表
model.fit(
    X, y,
    epochs=100,
    batch_size=32,
    validation_split=0.2,
    callbacks=[early_stopping]
)

K最近邻回归

KNN Regression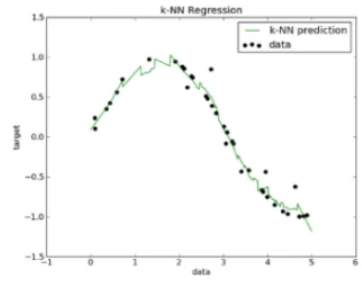

原理

局部加权平均：KNN回归是一种基于实例的学习方法，通过计算待预测样本与训练样本的距离，选择最近的K个样本进行预测。

预测公式：
$$ \hat{y} = \frac{1}{k}\sum_{i \in N_k(x)} y_i $$
其中：

$N_k(x)$ 是x的k个最近邻
$y_i$ 是第i个邻居的目标值

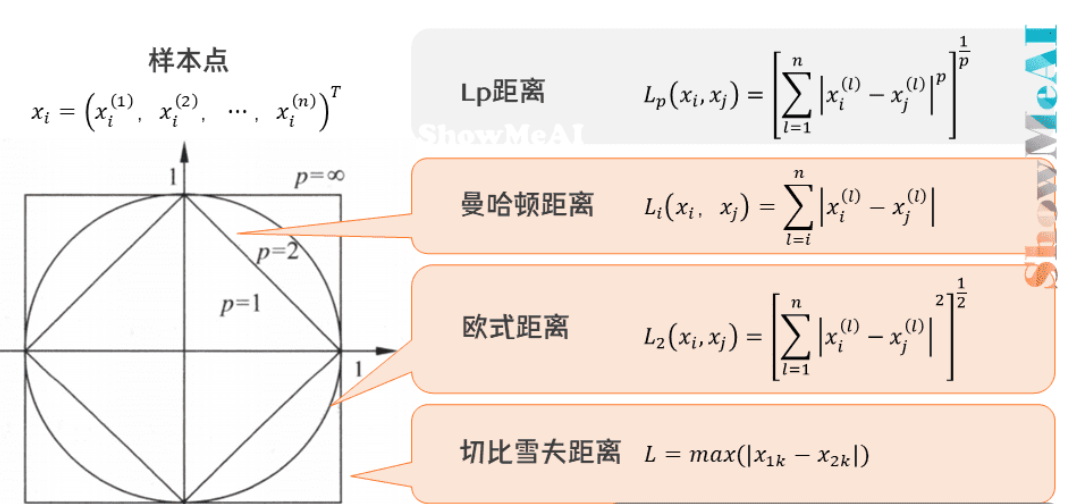
距离度量——闵可夫斯基距离：：
$$ D(x_i,x_j) = (\sum |x_i^{(m)} - x_j^{(m)}|^p)^{1/p} $$
其中：

$p=2$ 时为欧氏距离
$p=1$ 时为曼哈顿距离
$p=\infty$ 时为切比雪夫距离

优缺点

优点：简单易懂，对局部结构敏感。
缺点：计算复杂度高，对高维数据效果较差，需选择合适的K值。

Python示例

from sklearn.neighbors import KNeighborsRegressor
# 创建KNN回归模型
# n_neighbors: 邻居数量
# weights: 权重类型，可选：
#   - 'uniform': 统一权重，所有邻居的权重相等
#   - 'distance': 距离权重，根据距离的倒数计算权重
# algorithm: 计算最近邻的算法，可选：
#   - 'auto': 自动选择最佳算法
#   - 'ball_tree': 球树算法，适合高维数据
#   - 'kd_tree': KD树算法，适合低维数据
#   - 'brute': 暴力搜索，适合小数据集
# metric: 距离度量方式，可选：
#   - 'minkowski': 闵可夫斯基距离，可调整p参数
#   - 'euclidean': 欧氏距离，p=2的闵可夫斯基距离
#   - 'manhattan': 曼哈顿距离，p=1的闵可夫斯基距离
#   - 'chebyshev': 切比雪夫距离，p=∞的闵可夫斯基距离
model = KNeighborsRegressor(
    n_neighbors=5,
    weights='distance',
    algorithm='auto',
    metric='minkowski',
    p=2,                # 闵可夫斯基距离的幂参数
    n_jobs=-1          # 并行计算的作业数
)
model.fit(X_scaled, y)

回归模型对比总结

模型类型	训练速度	可解释性	非线性处理	特征选择	最佳场景
线性回归	S	S	❌	❌	线性关系数据
多项式回归	A	B	C	❌	低阶非线性
正则化回归	A	A	❌	✅	高维数据
分位数回归	C	B	D	❌	非常态分布
决策树	B	A	A	✅	结构化数据
随机森林	C	C	S	✅	通用场景
梯度提升	D	D	S	✅	高精度需求
SVR	D	❌	A	❌	小样本非线性
神经网络	E	❌	S	❌	复杂模式识别
KNN	E	D	B	❌	低维相似度分析

符号说明：字母表示能力强度，✅表示支持，❌表示不支持

模型选择指南：

数据量小+线性关系 → 线性回归
需要解释特征贡献 → 正则化回归
异方差/极端值 → 分位数回归
非结构化数据+高精度 → 梯度提升树（XGBoost/LightGBM）
小样本+非线性问题 → SVR
多模态复杂模式 → 神经网络
通用原型开发 → 随机森林

# 自动化模型选择工具例子
from sklearn.model_selection import cross_val_score
from sklearn.metrics import make_scorer, r2_score

# 定义模型字典
models = {
    'Linear': LinearRegression(
        fit_intercept=True,
        n_jobs=-1
    ),
    'RandomForest': RandomForestRegressor(
        n_estimators=100,
        max_depth=None,
        n_jobs=-1
    ),
    'XGBoost': xgb.XGBRegressor(
        objective='reg:squarederror',
        max_depth=5,
        learning_rate=0.1
    )
}

# 使用交叉验证评估模型
# cv: 交叉验证折数
# scoring: 评估指标
for name, model in models.items():
    scores = cross_val_score(
        model, X, y,
        cv=5,
        scoring='r2',
        n_jobs=-1
    )
    print(f"{name} R2分数: {scores.mean():.3f} (±{scores.std():.3f})")

秋月春风

明月守灯寻长梦，梦长寻灯守月明

明月守灯寻长梦，梦长寻灯守月明

秋月春风

线性回归

原理

特点

优缺点

应用领域

代码示例

多项式回归

原理

特点

优缺点

应用领域

代码示例

正则化回归

正则化原理

LASSO回归

原理

特点

代码示例

岭回归

原理

特点

代码示例

弹性网络回归

原理

特点

对比总结

代码示例

分位数回归

原理

优缺点

应用领域

代码示例

树模型回归

决策树回归

原理

代码示例

随机森林

原理

代码示例

梯度提升

原理

代码示例

对比总结

XGBoost

原理

代码示例

LightGBM

优化技术

代码示例

支持向量回归

原理

优缺点

应用领域

代码示例

神经网络回归

原理

优缺点

代码示例

K最近邻回归

原理

优缺点

回归模型对比总结